ECUACIONES PARAMÉTRICAS Y COORDENADAS POLARES

Cálculo de curvas paramétricas: Objetivos de aprendizaje

8.2.1. Determinar derivadas y ecuaciones de tangentes para curvas paramétricas.
8.2.2. Encuentre el área bajo una curva paramétrica.
8.2.3. Utilice la ecuación para la longitud de arco de una curva paramétrica.
8.2.4. Aplique la fórmula para el área de la superficie a un volumen generado por una curva paramétrica.

       Ahora que hemos introducido el concepto de curva parametrizada, nuestro siguiente paso es aprender a trabajar con este concepto en el contexto del cálculo. Por ejemplo, si conocemos una parametrización de una curva dada, ¿es posible calcular la pendiente de una recta tangente a la curva? ¿Qué tal la longitud del arco de la curva? ¿O el área debajo de la curva?

Otro escenario: supongamos que nos gustaría representar la ubicación de una pelota de béisbol después de que la pelota deja la mano de un lanzador. Si la posición de la pelota de béisbol está representada por la curva plana (x(t), y(t)), entonces deberíamos poder usar el cálculo para encontrar la velocidad de la pelota en un momento dado. Además, deberíamos poder calcular qué tan lejos ha viajado esa bola en función del tiempo. (Vea la solución de este problema).

Derivadas de ecuaciones paramétricas

Comenzamos preguntando cómo calcular la pendiente de una recta tangente a una curva paramétrica en un punto. Considere la curva plana definida por las ecuaciones paramétricas

x(t) = 2t + 3,  y(t) = 3t − 4,  −2 ≤ t ≤ 3.

El gráfico de esta curva aparece en la Figura 8.2_1. Es un segmento de recta que comienza en (−1, −10) y termina en (9, 5).

Podemos eliminar el parámetro resolviendo primero la ecuación x(t) = 2t + 3 para t:

Sustituyendo esto en y(t), obtenemos

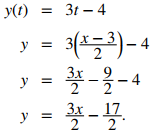
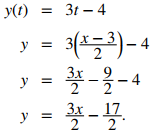
La pendiente de esta recta viene dada por dy/dx = 3/2. A continuación, calculamos x′(t)  y  y′(t). Esto da x′(t) = 2  y  y′(t) = 3. Darse cuenta de

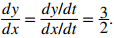
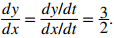
Esto no es una coincidencia, como se describe en el siguiente teorema.

TEOREMA 8.2.1 Derivada de ecuaciones paramétricas

Considere la curva plana definida por las ecuaciones paramétricas x = x(t)  e  y = y(t). Suponga que existen las derivadas x′(t)  e  y′(t), y suponga que x′(t) ≠ 0. Entonces la derivada dy/dx viene dada por

Prueba
Este teorema se puede probar usando la regla de la cadena. En particular, suponga que el parámetro t puede eliminarse, dando como resultado una función diferenciable y = F(x). Entonces y(t) = F(x(t)). Diferenciar ambos lados de esta ecuación usando la regla de la cadena produce

Pero F′(x(t)) = dy/dx, lo que prueba el teorema. ◊

---

La ecuación de este teorema 8.2.1 se puede utilizar para calcular derivadas de curvas planas, así como puntos críticos. Recuerde que un punto crítico de una función diferenciable y = f (x) es cualquier punto x = x₀ tal que f ′(x₀) = 0  o  f ′(x₀) no existe. Además esta ecuación da una fórmula para la obtención de la pendiente de una recta tangente a una curva definida paramétricamente independientemente de si la curva puede ser descrita por una función y = f (x) o no.

Ejemplo ilustrativo 8.2_1  Encontrar la derivada de una curva paramétrica

Calcule la derivada dy/dx para cada una de las siguientes curvas planas definidas paramétricamente y ubique los puntos críticos en sus respectivos gráficos.

Solución:
a.  Para aplicar la ecuación dada por el Teorema 8.2.1, primero calcule x′(t)  e  y′(t):

A continuación sustituya estas derivadas en la ecuación:

Esta derivada no está definida cuando t = 0. Al calcular x(0)  y  y(0) se obtiene x(0) = (0)² − 3 = −3  y  y(0) = 2(0)  − 1 = −1, que corresponde al punto (−3, −1) en la gráfica. La gráfica de esta curva es una parábola que abre hacia la derecha y el punto (−3, −1) es su vértice, como se muestra en la siguiente figura.

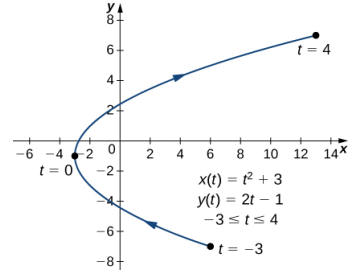
b.  Para aplicar la ecuación dada por el Teorema 8.2.1, primero calcule x′(t)  e  y′(t):

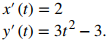
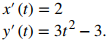
A continuación sustituya estas derivadas en la ecuación:

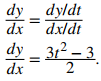
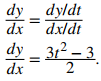
Esta derivada es cero cuando t = ± 1. Cuando t = −1 tenemos

x(−1) = 2(−1) + 1 = −1  y  y(−1) = (−1)³ − 3(−1) + 4 = −1 + 3 + 4 = 6,

que corresponde al punto (−1, 6) en el gráfico. Cuando t = 1 tenemos

x(1) = 2(1) + 1 = 3  y  y(1) = (1)³ − 3 (1) + 4 = 1 − 3 + 4 = 2,

que corresponde al punto (3, 2) del gráfico. El punto (3, 2) es un mínimo relativo y el punto (−1, 6) es un máximo relativo, como se ve en el siguiente gráfico.

c.  Para aplicar la ecuación dada por el Teorema 8.2.1, primero calcule x′(t)  e  y′(t):

A continuación sustituya estas derivadas en la ecuación:

Esta derivada es cero cuando cost = 0 y no está definida cuando sent = 0. Esto da t = 0, π/2, π, 3π/2 y 2π como puntos críticos para t. Sustituyendo cada uno de estos en x(t)  y  y(t), obtenemos

t	x(t)	y(t)
0	5	0
π/2	0	5
π	−5	0
3π/2	0	−5
2π	5	0

Estos puntos corresponden a los lados, arriba y abajo de la circunferencia que está representado por las ecuaciones paramétricas (Figura 8.2_4). En los bordes izquierdo y derecho del círculo, la derivada no está definida, y en la parte superior e inferior, la derivada es igual a cero.

Ejercicio de control 8.2_1

Calcule la derivada dy/dx para la curva plana definida por las ecuaciones

x(t) = t² − 4t,  y(t) = 2t³ − 6t,  −2 ≤ t ≤ 3

y ubica los puntos críticos en su gráfica.

Ejemplo ilustrativo 8.2_2 Encontrar una recta tangente

Encuentra la ecuación de la recta tangente a la curva definida por las ecuaciones

x(t) = t² − 3,  y(t) = 2t − 1, −3 ≤ t ≤ 4  cuando  t = 2.

Solución:
Primero encuentre la pendiente de la recta tangente usando la ecuación dada en el Teorema 8.2.1, lo que requiere calcular x′(t)  y  y′(t):

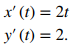
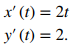
A continuación sustituya estas derivadas en la ecuación:

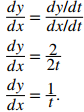
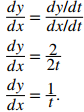
Cuando t = 2, dy/dx = 1/2, entonces esta es la pendiente de la recta tangente. Calculando x(2)  e  y(2)  se obtiene

x(2) = (2)² − 3 = 1  y  y(2) = 2(2) − 1 = 3, 

que corresponde al punto (1, 3) del gráfico (Figura 8.2_5). Ahora usa la forma punto-pendiente de la ecuación de una recta para encontrar la ecuación de la recta tangente:

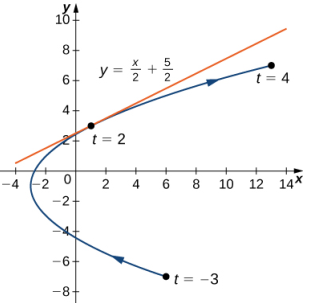
Ejercicio de control 8.2_2

Encuentra la ecuación de la recta tangente a la curva definida por las ecuaciones

x(t) = t² − 4t,  y(t) = 2t³ − 6t, −2 ≤ t ≤ 3   cuando  t = 5.

Derivadas de segundo orden

Nuestro próximo objetivo es ver cómo tomar la segunda derivada de una función definida paramétricamente. La segunda derivada de una función y = f (x) se define como la derivada de la primera derivada; es decir,

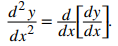
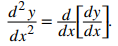
Ya que

podemos reemplazar la y en ambos lados de esta ecuación con dy/dx. Esto nos da

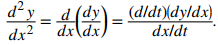
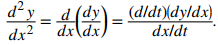
Si conocemos dy/dx en función de t, entonces esta fórmula es sencilla de aplicar.

Ejemplo ilustrativo 8.2_3 Encontrar una segunda derivada

Calcule la segunda derivada d²y/dx² para la curva plana definida por las ecuaciones paramétricas x(t) = t² − 3,  y(t) = 2t − 1, −3 ≤ t ≤ 4.

Solución:

Del Ejemplo ilustrativo 8.2_1 sabemos que dy/dx = 2/2t = 1/t. Usando la fórmula para hallar la segunda derivada de una ecuación paramétrica, obtenemos

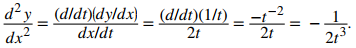
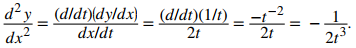
Ejercicio de control 8.2_3

Calcule la segunda derivada d²y/dx² para la curva plana definida por las ecuaciones

x(t) = t²  − 4t,  y(t) = 2t³ − 6t,  −2 ≤ t ≤ 3

y ubica los puntos críticos en su gráfica.

Integrales que involucran ecuaciones paramétricas

Ahora que hemos visto cómo calcular la derivada de una curva plana, la siguiente pregunta es la siguiente: ¿Cómo encontramos el área bajo una curva definida paramétricamente? Recuerde la cicloide definida por las ecuaciones x(t) = t − sent,  y(t) = 1 − cost. Suponga que queremos encontrar el área de la región sombreada en el siguiente gráfico.

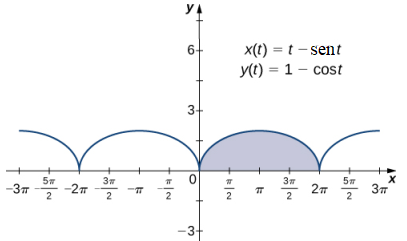
Derivar una fórmula para el área bajo la curva definida por las funciones

x = x(t),  y = y(t),  a ≤ t ≤ b,

asumimos que x(t) es diferenciable y comenzamos con una partición regular del intervalo a ≤ t ≤ b. Suponga que t₀ = a < t₁ < t₂ < ⋯ < tₙ = b  y considere la siguiente gráfica.

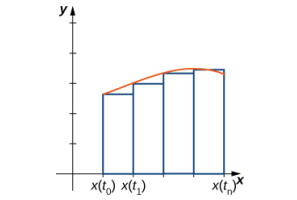
Usamos rectángulos para aproximar el área debajo de la curva. La altura de un rectángulo típico en esta parametrización es

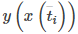
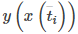
para algún valor 

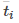
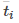
en el i-ésimo subintervalo, y el ancho se puede calcular como

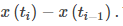
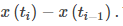
Así, el área del i-ésimo rectángulo está dada por

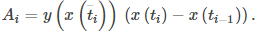
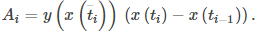
Entonces una suma de Riemann para el área es

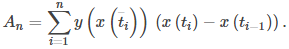
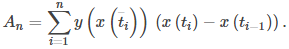
Multiplicar y dividir cada área por t_i − t_{i − 1} da

Tomando el límite cuando n tiende al infinito da

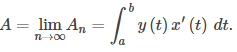
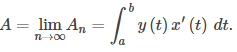
Esto lleva al siguiente teorema.

TEOREMA 8.2.2 Área bajo una curva paramétrica

Considere la curva plana que no se interseca automáticamente definida por las ecuaciones paramétricas x = x(t),  y = y(t),  a ≤ t ≤ b y suponga que x(t) es diferenciable. El área bajo esta curva está dada por

Ejemplo ilustrativo 8.2_4 Encontrar el área bajo una curva paramétrica

Encuentre el área bajo la curva de la cicloide definida por las ecuaciones

x(t) = t − sent,  y(t) = 1 − cost,  0 ≤ t ≤ 2π.

Solución:

Usando la ecuación para el área dada por el teorema 8.2.2, tenemos

Ejercicio de control 8.2_4

Encuentra el área bajo la curva del hipocicloide definida por las ecuaciones

x(t) = 3cost + cos3t,  y(t) = 3sent − sen3t,  0 ≤ t ≤ π.

Longitud de arco de una curva paramétrica

Además de encontrar el área bajo una curva paramétrica, a veces necesitamos encontrar la longitud de arco de una curva paramétrica. En el caso de un segmento de recta, la longitud del arco es la misma que la distancia entre los puntos finales. Si una partícula viaja del punto A al punto B a lo largo de una curva, entonces la distancia que recorre la partícula es la longitud del arco. Para desarrollar una fórmula para la longitud del arco, comenzamos con una aproximación por segmentos de recta como se muestra en el siguiente gráfico.

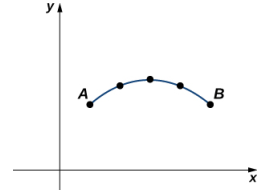
Dada una curva plana definida por las funciones x = x(t),  y = y(t),  a ≤ t ≤ b, comenzamos dividiendo el intervalo [a, b] en n subintervalos iguales: t₀ = a < t₁ < t₂ < ⋯ < tₙ= b. El ancho de cada subintervalo viene dado por Δt = (b − a)/n. Podemos calcular la longitud de cada segmento de recta:

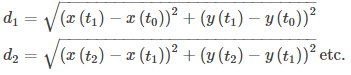
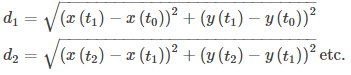
Luego sumarlos. Denotemos con s la longitud exacta del arco y sₙ la aproximación por n segmentos de recta:

Si asumimos que x(t)  y  y(t) son funciones diferenciables de t, entonces se aplica el Teorema del valor medio (Introducción a las aplicaciones de las derivadas), por lo que en cada subintervalo [t_{k − 1}, t_k] existen

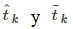
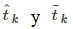
tal que

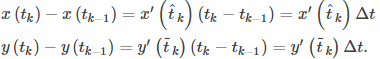
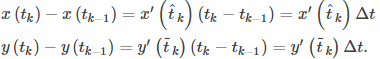
Por lo tanto, la ecuación 

se convierte en

Ésta es una suma de Riemann que se aproxima a la longitud del arco sobre una partición del intervalo [a, b]. Si asumimos además que las derivadas son continuas y dejamos que el número de puntos en la partición aumente sin límite, la aproximación tiende a la longitud exacta del arco. Esto da

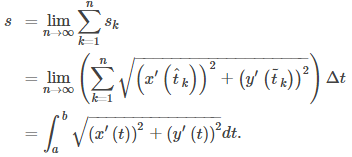
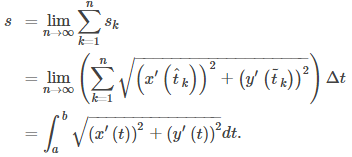
Al tomar el límite, los valores de

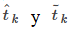
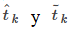
ambos están contenidos dentro del mismo intervalo cada vez más reducido de ancho Δt, por lo que deben converger al mismo valor.

Podemos resumir este método en el siguiente teorema.

TEOREMA 8.2.3 Longitud de arco de una curva paramétrica

Considere la curva plana definida por las ecuaciones paramétricas x = x(t),  y = y(t),  t₁ ≤ t ≤ t₂ y suponga que x(t)  y  y(t) son funciones diferenciables de t. Entonces la longitud del arco de esta curva viene dada por

En este punto, una derivación lateral conduce a una fórmula anterior para la longitud del arco. En particular, suponga que el parámetro se puede eliminar, lo que lleva a una función y = F(x). Entonces y(t) = F(x(t)) y la regla de la cadena da y′(t) = F′(x(t))x′(t). Sustituyendo esto en la Ecuación del Teorema 8.2.3 se obtiene

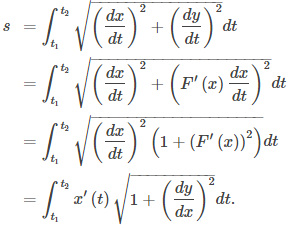
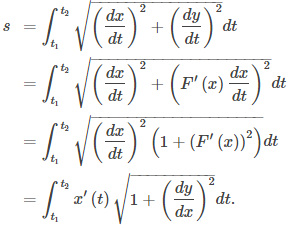
Aquí hemos asumido que x′(t) > 0, que es una suposición razonable. La regla de la cadena da dx = x′(t)dt, y dejando a = x(t₁)  y  b = x(t₂) obtenemos la fórmula

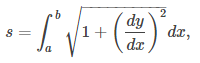
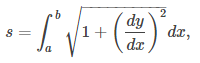
que es la fórmula para la longitud del arco obtenida en la Introducción a las Aplicaciones de la Integración.

Ejemplo ilustrativo 8.2_5  Encontrar la longitud del arco de una curva paramétrica

Encuentra la longitud del arco de la semicircunferencia definida por las ecuaciones

x(t) = 3cost,  y(t) = 3sent,  0 ≤ t ≤ π.

Solución:

Los valores t = 0  a  t = π trazan la curva roja en la figura 8.2_9. Para determinar su longitud, use la fórmula proporcionada en el teorema 8.2.3:

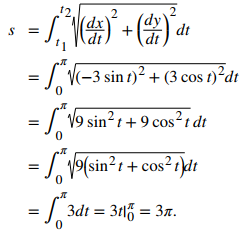
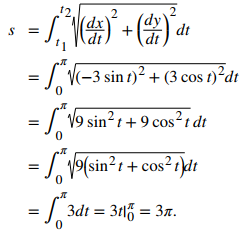
Tenga en cuenta que la fórmula para la longitud del arco de una semicircunferencia es πr y el radio de este círculo es 3. Este es un gran ejemplo del uso del cálculo para derivar una fórmula conocida de una cantidad geométrica.

Ejercicio de control 8.2_5

Encuentre la longitud del arco de la curva definida por las ecuaciones

x(t) = 3t²,  y(t) = 2t³,  1 ≤ t ≤ 3.

       Regresemos ahora al problema planteado al principio de la sección sobre una pelota de béisbol que sale de la mano de un lanzador. Ignorando el efecto de la resistencia del aire (¡a menos que sea una bola curva!), La bola viaja en una trayectoria parabólica. Suponiendo que la mano del lanzador está en el origen y la bola viaja de izquierda a derecha en la dirección del eje x positivo, las ecuaciones paramétricas para esta curva se pueden escribir como

x(t) = 140t,  y(t) = −16t² + 2t

donde t representa el tiempo. Primero calculamos la distancia que viaja la pelota en función del tiempo. Esta distancia está representada por la longitud del arco. Podemos modificar ligeramente la fórmula de la longitud del arco. Primero reescriba las funciones x(t) e y(t) usando v como variable independiente, para eliminar cualquier confusión con el parámetro t:

x(v) = 140v,  y(v) = −16v² + 2v

Luego escribimos la fórmula de la longitud del arco de la siguiente manera:

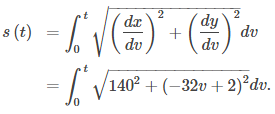
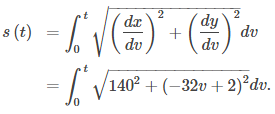
La variable v actúa como una variable ficticia que desaparece después de la integración, dejando la longitud del arco en función del tiempo t. Para integrar esta expresión podemos usar la siguiente fórmula dada en la Tabla de integrales,

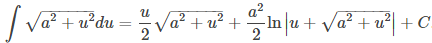
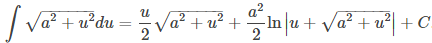
Establecemos a = 140  y  u = −32v + 2. Esto da du = −32dv, entonces dv = −(1/32)du. Por lo tanto

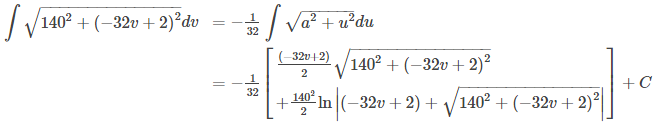
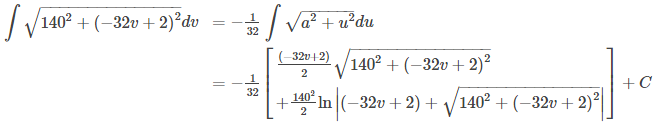
y

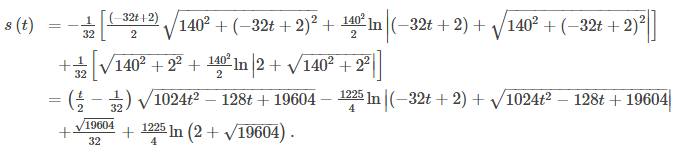
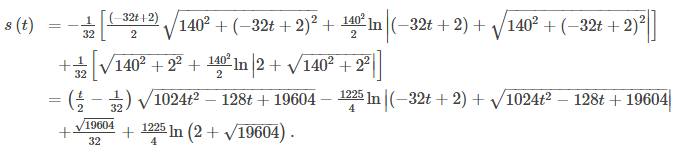
Esta función representa la distancia recorrida por la pelota en función del tiempo. Para calcular la velocidad, tome la derivada de esta función con respecto a t. Si bien esto puede parecer una tarea abrumadora, es posible obtener la respuesta directamente del Teorema fundamental del cálculo:

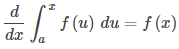
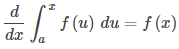
Por lo tanto

Un tercio de segundo después de que la pelota abandona la mano del lanzador, la distancia que recorre es igual a

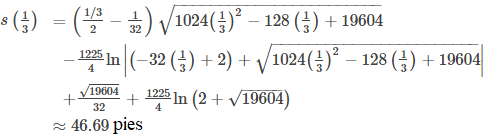
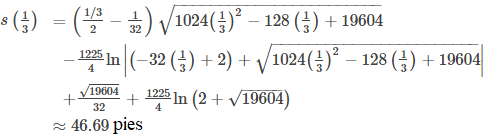
Este valor es un poco más de las tres cuartas partes del camino al plato de home. La velocidad de la pelota es

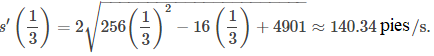
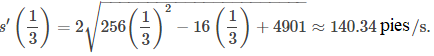
Esta velocidad se traduce en aproximadamente 95 mph, una bola rápida de grandes ligas.

Área de superficie generada por una curva paramétrica

Recuerde el problema de encontrar el área de superficie de un volumen de revolución. En Longitud de curva y área de superficie, derivamos una fórmula para encontrar el área de superficie de un volumen generado por una función y = f (x) desde x = a hasta x = b, girado alrededor del eje x:

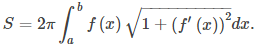
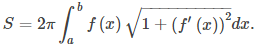
Ahora consideramos un volumen de revolución generado al girar una curva definida paramétricamente x = x(t),  y = y(t),  a ≤ t ≤ b alrededor del eje x, como se muestra en la siguiente figura.

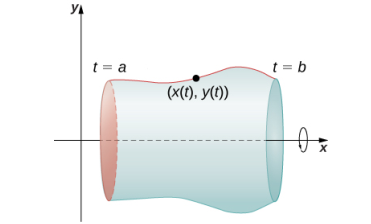
La fórmula análoga para una curva definida paramétricamente es

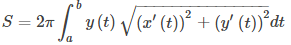
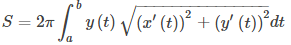
siempre que y(t) no sea negativo en [a, b].

Ejemplo ilustrativo 8.2_6  Encontrar el área de una superficie

Encuentre el área de la superficie de una esfera de radio r centrada en el origen.

Solución:
Partimos de la curva definida por las ecuaciones

x(t) = rcost,  y(t) = rsent,  0 ≤ t ≤ π.

Esto genera una semicircunferencia superior de radio r centrado en el origen como se muestra en el siguiente gráfico.

Cuando esta curva gira alrededor del eje x, genera una esfera de radio r. Para calcular el área de la superficie de la esfera, usamos la fórmula del área de superficie generada por una curva paramétrica:

Esta es, de hecho, la fórmula conocida para el área de superficie de una esfera.

Ejercicio de control 8.2_6

Encuentre el área de superficie generada cuando la curva plana definida por las ecuaciones

x(t) = t³,  y(t) = t²,  0 ≤ t ≤ 1

gira alrededor del eje x.