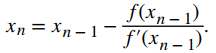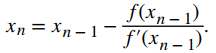MÉTODO DE NEWTON: Objetivos de aprendizaje
4.9.1. Describir los pasos del método de Newton.
4.9.2. Explicar qué significa un proceso iterativo.
4.9.3. Reconocer cuándo el método de Newton no funciona.
4.9.4. Aplicar procesos iterativos a diversas situaciones.
En muchas áreas de las matemáticas puras y aplicadas, estamos interesados en encontrar soluciones a una ecuación de la forma f (x) = 0. Para la mayoría de las funciones, sin embargo, es difícil, si no imposible, calcular sus ceros explícitamente. En esta sección, veremos una técnica que proporciona una forma muy eficiente de aproximar los ceros de las funciones. Esta técnica hace uso de aproximaciones de rectas tangentes y está detrás del método utilizado a menudo por calculadoras y computadoras para encontrar ceros.
Describiendo el método de Newton
Considere la tarea de encontrar las soluciones de f (x) = 0. Si f es el polinomio de primer grado f (x) = ax + b, entonces la solución de f (x) = 0 viene dada por la fórmula x = −b/a.
Si f es el polinomio de segundo grado f (x) = ax2 + bx + c, las soluciones de f (x) = 0 se pueden encontrar usando la fórmula cuadrática. Sin embargo, para polinomios de grado 3 o mayor, encontrar raíces de f se vuelve más complicado. Aunque existen fórmulas para polinomios de tercer y cuarto grado, son bastante complicadas. Además, si f es un polinomio de grado 5 o mayor, se sabe que no existen tales fórmulas. Por ejemplo, considere la función


No existe una fórmula que nos permita encontrar las soluciones de f (x) = 0. Existen dificultades similares para las funciones no polinómicas. Por ejemplo, considere la tarea de encontrar soluciones de tan(x) − x = 0. No existe una fórmula simple para las soluciones de esta ecuación. En casos como estos, podemos usar el método de Newton para aproximar las raíces.
Método numérico de Newton
El método de Newton utiliza la siguiente idea para aproximar las soluciones de f (x) = 0. Al trazar la gráfica de f, podemos estimar una raíz de f (x) = 0. Llamemos a esta estimación x0. Luego dibujamos la recta tangente a f en x0. Si f ′ (x0) ≠ 0, esta recta tangente intersecta el eje x en algún punto (x1, 0). Ahora dejemos que x1 sea la próxima aproximación a la raíz real. Normalmente, x1 está más cerca que x0 de una raíz real. Luego dibujamos la recta tangente a f en x1. Si f ′ (x1) ≠ 0, esta recta tangente también se cruza con el eje x, produciendo otra aproximación, x2. Continuamos de esta manera, derivando una lista de aproximaciones: x0, x1, x2,… .Típicamente, los números x0, x1, x2,….se acercan rápidamente a una raíz real x *, como se muestra en la siguiente figura
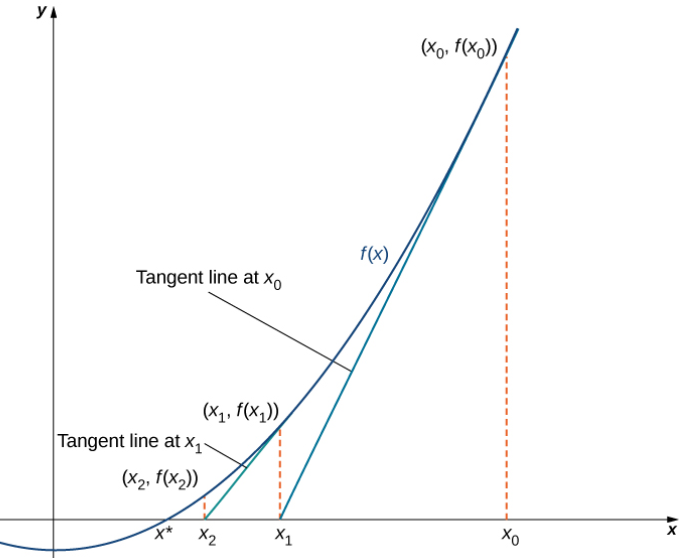
Ahora veamos cómo calcular las aproximaciones x0, x1, x2,… .Si x0 es nuestra primera aproximación, la aproximación x1 se define dejando que (x1, 0) sea la intersección x de la recta tangente a f en x0. La ecuación de esta recta tangente viene dada por


Por lo tanto, x1 debe satisfacer
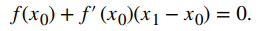
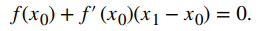
Resolviendo esta ecuación para x1, concluimos que
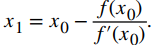
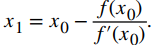
De manera similar, el punto (x2, 0) es la intersección x de la línea tangente a f en x1. Por lo tanto, x2 satisface la ecuación


En general, para n > 0, xn satisface