| 9. Ecuaciones diferenciales | 9.5 Ecuaciones lineales de segundo orden |
9.5.4 El método de coeficientes indeterminados I
En esta sección consideramos la ecuación de coeficientes constantes
ay′′ + by′ + cy = eαxG(x), (9.5.4.1)
donde α es una constante y G es un polinomio.
Del Teorema 9.5.3.2, la solución general de (9.5.4.1) es y = yp + c1y1 + c2y2, donde yp es una solución particular de (9.5.4.1) y {y1, y2} es un conjunto fundamental de soluciones de la ecuación complementaria
ay′′ + by′ + cy = 0.
En la Sección 9.5.2 mostramos cómo encontrar {y1, y2}. En esta sección mostraremos cómo encontrar yp. El procedimiento que usaremos se llama método de coeficientes indeterminados.
Nuestro primer ejemplo es similar a los Ejercicios 16 a 21.
Ejemplo ilustrativo 9.5.4.1
Encuentre una solución particular de
y′′ − 7y′ + 12y = 4e2x. (9.5.4.2)
Luego encuentra la solución general.
Solución:
Sustituir yp = Ae2x por y en (9.5.4.2) producirá un múltiplo constante de Ae2x en el lado izquierdo de (9.5.4.2), por lo que es posible elegir A para que yp sea una solución de (9.5.4.2). Vamos a intentarlo; si yp = Ae2x entonces
yp′′ − 7yp′ + 12yp = 4Ae2x − 14Ae2x + 12Ae2x = 2Ae2x = 4e2x
si A = 2. Por lo tanto yp = 2e2x es una solución particular de (9.5.4.2). Para encontrar la solución general, notamos que el polinomio característico de la ecuación complementaria
y′′ − 7y′ + 12y = 0 (9.5.4.3)
es p(r) = r2 − 7r + 12 = (r − 3)(r − 4), entonces {e3x, e4x} es un conjunto fundamental de soluciones de (9.5.4.3).
Por tanto, la solución general de (9.5.4.2) es
y = 2e2x + c1e3x + c2e4x. ♦
Ejemplo ilustrativo 9.5.4.2
Encuentre una solución particular de
y′′ − 7y′ + 12y = 5e4x. (9.5.4.4)
Luego encuentra la solución general.
Solución:
Recién llegado de nuestro éxito al encontrar una solución particular de (9.5.4.2), donde elegimos yp = Ae2x porque el lado derecho de (9.5.4.2) es un múltiplo constante de e2x, puede parecer razonable probar yp = Ae4x como solución particular de (9.5.4.4). Sin embargo, esto no funcionará, ya que vimos en el ejemplo 9.5.4.1 que e4x es una solución de la ecuación complementaria (9.5.4.3), por lo que sustituir yp = Ae4x en el lado izquierdo de (9.5.4.4) produce cero en el izquierdo, no importa cómo elijamos A. Para descubrir una forma adecuada para yp, utilizamos el mismo enfoque que empleamos. en la Sección 9.5.2 para encontrar una segunda solución de
ay′′ + by′ + cy = 0
en el caso de que la ecuación característica tenga raíz real repetida: buscamos soluciones de (9.5.4.4) en la forma y = ue4x, donde u es una función a determinar. Sustituyendo
y = ue4x, y′ = u′e4x + 4ue4x, y y′′ = u′′e4x + 8u′e4x + 16ue4x (9.5.4.5)
en (9.5.4.4) y cancelando el factor común e4x se obtiene
(u′′ + 8u′ + 16u) − 7(u′ + 4u) + 12u = 5,
o
u′′ + u′ = 5.
Por inspección vemos que up = 5x es una solución particular de esta ecuación, por lo que yp = 5xe4x es una solución particular de (9.5.4.4). Por lo tanto
y = 5xe4x + c1e3x + c2e4x
es la solución general. ♦
Ejemplo ilustrativo 9.5.4.3
Encuentre una solución particular de
y′′ − 8y′ + 16y = 2e4x. (9.5.4.6)
Solución:
Dado que el polinomio característico de la ecuación complementaria
y′′ − 8y′ + 16y = 0 (9.5.4.7)
es p(r) = r2 − 8r + 16 = (r − 4)2, tanto y1 = e4x como y2 = xe4x son soluciones de (9.5.4.7). Por lo tanto (9.5.4.6) no tiene solución de la forma yp = Ae4x o yp = Axe4x. Como en el Ejemplo 9.5.4.2, buscamos soluciones de (9.5.4.6) en la forma y = ue4x, donde u es una función a determinar. Sustituyendo de (9.5.4.5) en (9.5.4.6) y cancelando el factor común e4x se obtiene
(u′′ + 8u′ + 16u) − 8(u′ + 4u) + 16u = 2,
o
u′′ = 2.
Al integrar dos veces y tomar las constantes de integración como cero, se muestra que up = x2 es una solución particular de esta ecuación, por lo que yp = x2e4x es una solución particular de (9.5.4.4). Por lo tanto
y = e4x(x2 + c1 + c2x)
es la solución general. ♦
Los ejemplos anteriores ilustran los siguientes hechos relacionados con la forma de una solución particular yp de una ecuación de coeficientes constantes de segundo orden de la forma
ay′′ + by′ + cy = keαx,
donde k es una constante distinta de cero:
(a) Si eαx no es una solución de la ecuación complementaria
ay′′ + by′ + cy = 0, (9.5.4.8)
entonces yp = Aeαx, donde A es una constante. (Ver Ejemplo 9.5.4.1).
(b) Si eαx es una solución de (9.5.4.8) pero xeαx no lo es, entonces yp= Axeαx, donde A es una constante. (Ver Ejemplo 9.5.4.2.)
(c) Si tanto eαx como xeαx son soluciones de (9.5.4.8), entonces yp = Ax2eαx, donde A es una constante. (Ver Ejemplo 9.5.4.3.)
Véase el ejercicio 30 para las demostraciones de estos hechos.
En los tres casos, puede simplemente sustituir la forma apropiada de yp y sus derivadas directamente en
ayp′′ + byp′ + cyp = keαx,
y despeje la constante A, como hicimos en el Ejemplo 9.5.4.1. (Consulte los ejercicios 31 a 33). Sin embargo, si la ecuación es
ayp′′ + byp′ + cyp = keαxG(x)
donde G es un polinomio de grado mayor que cero, le recomendamos que use la sustitución y = ueαx como hicimos en los Ejemplos 9.5.4.2 y 9.5.4.3. La ecuación para u resultará ser
au′′ + p′(α)u′ + p(α)u = G(x), (9.5.4.9)
donde p(r) = ar2 + br + c es el polinomio característico de la ecuación complementaria y p′(r) = 2ar + b (Ejercicio 30); sin embargo, no debes memorizar esto ya que es fácil derivar la ecuación para u en cualquier caso particular. Nótese, sin embargo, que si eαx es una solución de la ecuación complementaria entonces p(α) = 0, entonces (9.5.4.9) se reduce a
au′′ + p′(α)u′ = G(x),
mientras que si tanto eαx como xeαx son soluciones de la ecuación complementaria entonces p(r) = a(r − α)2 y p′(r) = 2a(r − α), entonces p(α) = p′(α) = 0 y (9.5.4.9) se reduce a
au′′ = G(x).
Ejemplo ilustrativo 9.5.4.4
Encuentre una solución particular de
y′′ − 3y′ + 2y = e3x(−1 + 2x + x2). (9.5.4.10)
Solución:
Sustituyendo
y = ue3x, y′ = u′e3x + 3ue3x, y y′′ = u′′e3x + 6u′e3x + 9ue3x
en (9.5.4.10) y cancelandoe3x, se obtiene
(u′′ + 6u′ + 9u) − 3(u′ + 3u) + 2u = −1 + 2x + x2,
o
u′′ + 3u′ + 2u = −1 + 2x + x2. (9.5.4.11)
Como en el Ejemplo 2, para adivinar una forma para una solución particular de (9.5.4.11), observamos que al sustituir u por un polinomio de segundo grado up = A + Bx + Cx2 en el lado izquierdo de (9.5.4.11) se produce otro polinomio de segundo grado con coeficientes que dependen de A, B y C; de este modo,
si up = A + Bx + Cx2 entonces u′p = B + 2Cx y u′′p = 2C.
Si up es para satisfacer (9.5.4.11), debemos tener


Igualando coeficientes de potencias iguales de x en los dos lados de la última igualdad se obtiene
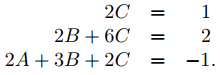
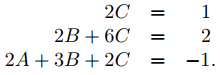
Resolviendo estas ecuaciones para C, B y A (en ese orden) se obtiene C = 1/2, B = −1/2, A = −1/4.
Por lo tanto
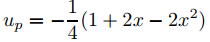
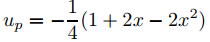
es una solución particular de (9.5.4.11), y
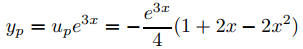
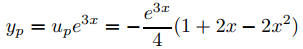
es una solución particular de (9.5.4.10). ♦
Ejemplo ilustrativo 9.5.4.5
Encuentre una solución particular de
y′′ − 4y′ + 3y = e3x(6 + 8x + 12x2). (9.5.4.12)
Solución:
Sustituyendo
y = ue3x, y′ = u′e3x + 3ue3x, y y′′ = u′′e3x + 6u′e3x + 9ue3x
en (9.5.4.12) y cancelando e3x, se obtiene
(u′′ + 6u′ + 9u) − 4(u′ + 3u) + 3u = 6 + 8x + 12x2,
o
u′′ + 2u′ = 6 + 8x + 12x2. (9.5.4.13)
No hay término u en esta ecuación, ya que e3x es una solución de la ecuación complementaria para (9.5.4.12). (Consulte el ejercicio 30). Por lo tanto, (9.5.4.13) no tiene una solución particular de la forma up = A + Bx + Cx2 que usamos con éxito en el ejemplo 9.5.4.4, ya que con esta elección de up,
u′′p + 2u′p = 2C + (B + 2Cx)
no puede contener el último término (12x2) en el lado derecho de (9.5.4.13). En su lugar, probemos up = Ax + Bx2 + Cx3 sobre la base de que
u′p = A + 2Bx + 3Cx2 y u′′p = 2B + 6Cx
juntos contienen todas las potencias de x que aparecen en el lado derecho de (9.5.4.13).
Sustituyendo estas expresiones en lugar de u′ y u′′ en (9.5.4.13), se obtiene
(2B + 6Cx) + 2(A + 2Bx + 3Cx2) = (2B + 2A) + (6C + 4B)x + 6Cx2 = 6 + 8x + 12x2.
La comparación de coeficientes de potencias iguales de x en los dos lados de la última igualdad muestra que up satisface (9.5.4.13) si


Resolviendo estas ecuaciones sucesivamente se obtiene C = 2, B = −1 y A = 4. Por lo tanto
up = x(4 − x + 2x2)
es una solución particular de (9.5.4.13), y
yp = upe3x = xe3x(4 − x + 2x2)
es una solución particular de (9.5.4.12). ♦
Ejemplo ilustrativo 9.5.4.6
Encuentre una solución particular de
4y′′ + 4y′ + y = e−x/2(−8 + 48x + 144x2). (9.5.4.14)
Solución:
Sustituyendo 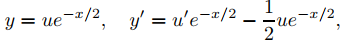
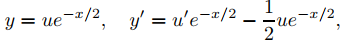


en (9.5.4.14) y cancelando e−x/2, se obtiene


o
u′′ = −2 + 12x + 36x2, (9.5.4.15)
que no contiene ni u ni u′ porque e−x/2 y xe−x/2 son ambas soluciones de la ecuación complementaria. (Véase el ejercicio 30.) Para obtener una solución particular de (9.5.4.15) integramos dos veces, tomando las constantes de integración como cero; de este modo,
u′p = −2x + 6x2 + 12x3 y up = −x2 + 2x3 + 3x4 = x2(−1 + 2x + 3x2).
Por lo tanto
yp = upe−x/2 = x2e−x/2(−1 + 2x + 3x2)
es una solución particular de (9.5.4.14). ♦
Resumen
Los ejemplos anteriores ilustran los siguientes hechos relacionados con soluciones particulares de una ecuación de coeficientes constantes de la forma
ay′′ + by′ + cy = eαxG(x),
(a) Si eαx no es una solución de la ecuación complementaria
ay′′ + by′ + cy = 0, (9.5.4.16)
entonces yp = eαxQ(x), donde Q es un polinomio del mismo grado que G. (Ver Ejemplo 9.5.4.4).
(b) Si eαx es una solución de (9.5.4.16) pero xeαx no lo es, entonces yp = xeαxQ(x), donde Q es un polinomio del mismo grado que G. (Vea el Ejemplo 9.5.4.5.)
(c) Si tanto eαx como xeαx son soluciones de (9.5.4.16), entonces yp = x2eαxQ(x), donde Q es un polinomio del mismo grado que G. (Consulte el ejemplo 9.5.4.6).
En los tres casos, puede simplemente sustituir la forma apropiada de yp y sus derivadas directamente en
ayp′′ + byp′ + cyp = eαxG(x),
y resuelve los coeficientes del polinomio Q. Sin embargo, si intentas esto, verás que los cálculos son más tediosos que los que encuentras al hacer la sustitución y = ueαx y encontrar una solución particular de la ecuación resultante para u. (Véanse los ejercicios 34 a 36). En el caso (a), la ecuación para u tendrá la forma
au′′ + p′(α)u′ + p(α)u = G(x),
con una solución particular de la forma up = Q(x), un polinomio del mismo grado que G, cuyos coeficientes se pueden encontrar por el método utilizado en el Ejemplo 9.5.4.4. En el Caso (b) la ecuación para u será de la forma
au′′ + p′(α)u′ = G(x)
(sin término u a la izquierda), con una solución particular de la forma up = xQ(x), donde Q es un polinomio del mismo grado que G cuyos coeficientes se pueden encontrar por el método usado en el ejemplo 9.5.4.5. En el Caso (c) la ecuación para u será de la forma
au′′ = G(x)
con una solución particular de la forma up = x2Q(x) que puede obtenerse integrando G(x)/a dos veces y tomando las constantes de integración como cero, como en el ejemplo 9.5.4.6. ♦
Usando el principio de superposición
El siguiente ejemplo muestra cómo combinar el método de coeficientes indeterminados y el Teorema 9.5.3.3, el principio de superposición.
Ejemplo ilustrativo 9.5.4.7
Encuentre una solución particular de
y′′ − 7y′ + 12y = 4e2x + 5e4x. (9.5.4.17)
Solución:
En el Ejemplo 9.5.4.1 encontramos que yp1 = 2e2x es una solución particular de
y′′ − 7y′ + 12y = 4e2x
y en el Ejemplo 9.5.4.2 encontramos que yp2 = 5xe4x es una solución particular de
y′′ − 7y′ + 12y = 5e4x
Por tanto, el principio de superposición implica que yp = 2e2x + 5xe4x es una solución particular de (9.5.4.17). ♦
