Reglas de diferenciación: Objetivos de aprendizaje
3.3.1 Indique las reglas de constante, múltiplo constante y potencia.
3.3.2. Aplica las reglas de suma y diferencia para combinar derivadas.
3.3.3 Use la regla del producto para encontrar la derivada de un producto de funciones.
3.3.4 Use la regla del cociente para encontrar la derivada de un cociente de funciones.
3.3.5. Extienda la regla de potencia a funciones con exponentes negativos.
3.3.6. Combina las reglas de diferenciación para encontrar la derivada de una función polinómica o racional.
Encontrar derivadas de funciones usando la definición de la derivada puede ser un proceso largo y, para ciertas funciones, bastante desafiante. Por ejemplo, anteriormente encontramos que


mediante el uso de un proceso que implicaba multiplicar una expresión por un conjugado antes de evaluar un límite. El proceso que podríamos usar para evaluar


aplicando la definición de derivada, aunque similar, es más complicado. En esta sección, desarrollamos reglas para encontrar derivadas que nos permitan evitar este proceso. Comenzamos con lo básico.
Las reglas básicas de derivación
Las funciones f (x) = c y g(x) = xⁿ donde n es un entero positivo son los bloques de construcción a partir de los cuales se construyen todos los polinomios y funciones racionales. Para encontrar derivadas de polinomios y funciones racionales de manera eficiente sin recurrir a la definición por límites de la derivada, primero debemos desarrollar fórmulas para diferenciar estas funciones básicas.
La regla de la constante
Primero aplicamos la definición de límite de la derivada para encontrar la derivada de la función constante, f (x) = c. Para esta función, tanto f (x) = c como f (x + h) = c, entonces obtenemos el siguiente resultado:


La regla para diferenciar funciones constantes se llama regla de la constante. Establece que la derivada de una función constante es cero; es decir, dado que una función constante es una recta horizontal, la pendiente, o la tasa de cambio, de una función constante es 0. Reformulamos esta regla en el siguiente teorema.
Teorema 3.3.1. Regla de la constante
|
Sea c una constante.Si f (x) = c, entonces f ′(c) = 0.Alternativamente, podemos expresar esta regla como
|
Ejemplo ilustrativo 3.3_1. Aplicando la regla de la constante
Encuentre la derivada de f (x) = 8.
Solución:
Esta es solo una aplicación de un paso de la regla:
f ′(x) = 0.
◊
La regla de la potencia
Anteriormente hemos mostrado que


En este punto, es posible que vea un patrón que comienza a desarrollarse para derivadas de la forma d/dx (xⁿ).
Continuamos nuestro examen de fórmulas derivadas diferenciando funciones de potencia de la forma f (x) = xⁿ donde n es un número entero positivo. Desarrollamos fórmulas para derivadas de este tipo de función en etapas, comenzando con potencias enteras positivas. Antes de establecer y probar la regla general para derivadas de funciones de esta forma, veamos un caso específico, d/dx (x³). A medida que avanzemos en este proceso de derivación, tenga en cuenta que la técnica utilizada en este caso es esencialmente la misma que la técnica utilizada para probar el caso general.
Ejemplo ilustrativo 3.3_2. Diferenciando x ³
Encuentra d/dx (x³)).
Solución:
Aplicamos la definición por límites de la derivada:


Expandimos (x + h)³ y observe que el primer término en la expansión de
(x + h)³ es x³ y el segundo término es 3x²h. Los siguientes términos contienen potencias de h que son de grado dos o mayor:


En el próximo paso cancelamos los términos x³, quedando sólo términos que contienen h:
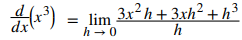
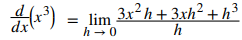
Sacamos el factor común h:


Después de cancelar el factor común h, observamos que el único término que no contiene h es 3x²:


Por último, evaluamos el límite (deje h ir a 0):
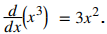
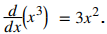
◊
Como veremos, el procedimiento para encontrar la derivada de la forma general f (x) = xⁿ es muy similar al usado en el ejemplo ilustrativo anterior. Aunque a menudo no es prudente sacar conclusiones generales de ejemplos específicos, observamos que cuando diferenciamos f (x) = x³, el exponente en x se convierte en el coeficiente de x² en la derivada y el exponente en x en la derivada disminuye en 1. El siguiente teorema establece que la regla para derivar una potencia es válida para todas las potencias enteras positivas de x. Eventualmente extenderemos este resultado a potencias enteras negativas. Más adelante, veremos que esta regla también puede extenderse primero a las potencias racionales de x y luego a los potencias arbitrarios de x. Sin embargo, tenga en cuenta que esta regla no se aplica a las funciones en las que una constante se eleva a un exponente variable, como f (x) = 3ᵡ.
TEOREMA 3.3.2. Regla de la potencia
|
Sea n un número entero positivo. Si f (x) = xⁿ, entonces
Alternativamente, podemos expresar esta regla como
|
Demostración:Para f (x) = xⁿ donde n es un entero positivo, tenemos
|
Ejemplo ilustrativo 3.3_3. Aplicando la Regla de la potencia
Encuentre la derivada de la función f (x) = x¹⁰ aplicando la regla de la potencia.
Solución:
Usando la regla de potencia con n = 10, obtenemos
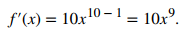
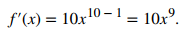
Reglas de la suma, la diferencia y los múltiplos constantes de funciones
Encontramos nuestras siguientes reglas de diferenciación al observar derivadas de sumas, diferencias y múltiplos constantes de funciones. Al igual que cuando trabajamos con funciones, existen reglas que facilitan la búsqueda de derivadas de funciones que sumamos, restamos o multiplicamos por una constante. Estas reglas se resumen en el siguiente teorema.
TEOREMA 3.3.3. Reglas para la derivación de la suma, la diferencia y múltiplos constantes
|
Supongamos que f (x) y g(x) son funciones diferenciables y k sea una constante. Entonces se cumplen cada una de las siguientes ecuaciones. Regla de suma. La derivada de la suma de una función f y una función g es la misma que la suma de la derivada de f y la derivada de g:
es decir, para
Regla de la diferencia. La derivada de la diferencia de una función f y una función g es la misma que la diferencia de la derivada de f y la derivada de g:
es decir, para
Regla del múltiplo constante. La derivada de una una función f multiplicada por una constante k es la misma que la constante multiplicada por la derivada de f:
es decir, para
|
Demostración:Aquí sólo proporcionamos la prueba de la regla de la suma. El resto sigue de manera similar. Para las funciones diferenciables f (x) y g(x), establecemos j(x) = f (x) + g(x). Usando la definición de la derivada por el límite tenemos |
Ejemplo ilustrativo 3.3_4. Aplicando la Regla del Múltiplo Constante
Encuentre la derivada de g(x) = 3x² y compárela con la derivada de f (x) = x².
Solución:
Usamos la regla de la potencia directamente:


Como f (x) = x² tiene derivada f ′(x) = 2x, vemos que la derivada de g(x) es 3 veces la derivada de f (x). Esta relación se ilustra en la figura 3.3_1.




Figura 3.3_1 La derivada de g(x) es 3 veces la derivada de f (x).
Ejemplo ilustrativo 3.3_5. Aplicación de reglas de derivadas básicas
Halle la derivada de f (x) = 2x⁵ + 7.
Solución:
Comenzamos aplicando la regla para diferenciar la suma de dos funciones, seguida de las reglas para diferenciar múltiplos constantes de funciones y la regla para diferenciar potencias. Para comprender mejor la secuencia en la que se aplican las reglas de diferenciación, utilizamos la notación Leibniz en toda la solución: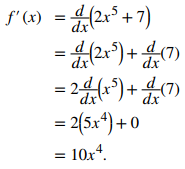
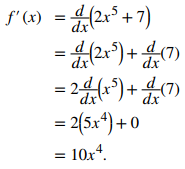
Ejemplo ilustrativo 3.3_6. Encontrar la ecuación de una recta tangente
Halle la ecuación de la recta tangente a la gráfica de f (x) = x² − 4x + 6 en x = 1.
Solución:
Para encontrar la ecuación de la recta tangente, necesitamos un punto y la pendiente. Para encontrar el punto, calcule


Esto nos da el punto (1, 3). Como la pendiente de la recta tangente en 1 es f ′(1), primero debemos encontrar f ′(x). Usando las propiedades de la derivada, obtenemos


entonces la pendiente de la recta tangente es f ′(1) = – 2. Usando la fórmula punto-pendiente de la recta, vemos que la ecuación de la recta tangente es


Poniendo la ecuación de la recta en forma pendiente-intersección, obtenemos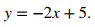
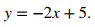


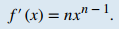






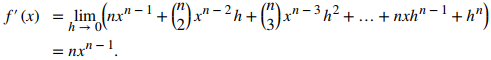

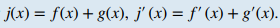
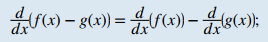
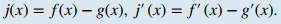






Gracias. El sitio web está construido usando un tema profesional que adquirí, se llama Savona Lite.
Realmente estoy disfrutando el diseño y el diseño de su sitio web. Es muy fácil de ver, lo que hace que sea mucho más agradable para mí venir aquí y visitarlo con más frecuencia. ¿Contrataste a un diseñador para crear tu tema? ¡Excelente trabajo!
Gracias. El sitio web está construido usando un tema profesional que adquirí, se llama Savona Lite.