| 9. Ecuaciones diferenciales | 9.10. Sistemas lineales de ecuaciones diferenciales |
9.10.5 Sistemas homogéneos con coeficientes constantes II
Vimos en la Sección 9.10.4 que si una matriz constante A de n × n tiene n valores propios reales λ1, λ2, . . . , λn (que no es necesario que sean distintos) con vectores propios asociados linealmente independientes x1, x2, . . . , xn, entonces la solución general de y′ = Ay es
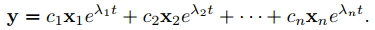
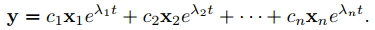
En esta sección consideramos el caso donde A tiene n valores propios reales, pero no tiene n vectores propios linealmente independientes. En álgebra lineal se muestra que esto ocurre si y solo si A tiene al menos un valor propio de multiplicidad r > 1 tal que el espacio propio asociado tiene una dimensión menor que r. En este caso se dice que A es defectuosa. Dado que está más allá del alcance de este libro dar un análisis completo de sistemas con matrices de coeficientes defectuosas, restringiremos nuestra atención a algunos casos especiales que ocurren comúnmente.
Ejemplo ilustrativo 9.10.5.1
Demuestre que el sistema
(9.10.5.1)
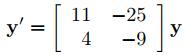
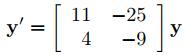
no tiene un conjunto fundamental de soluciones de la forma {x1eλ1t, x2eλ2t}, donde λ1 y λ2 son valores propios de la matriz de coeficientes A de (9.10.5.1) y x1, y x2 son vectores propios linealmente independientes asociados.
Solución:
El polinomio característico de A es
Por tanto, λ = 1 es el único valor propio de A. La matriz aumentada del sistema (A − I)x = 0 es
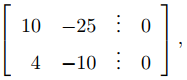
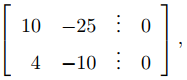
que es equivalente por filas a
Por lo tanto, x1 = 5x2/2 donde x2 es arbitrario. Por lo tanto, todos los vectores propios de A son múltiplos escalares de x1 = 
, por lo que A no tiene un conjunto de dos vectores propios linealmente independientes. ♦
Del Ejemplo 9.10.5.1, sabemos que todos los múltiplos escalares de y1 = et son soluciones de (9.10.5.1); sin embargo, para encontrar la solución general debemos encontrar una segunda solución y2 tal que {y1, y2} sea linealmente independiente. Teniendo presente el procedimiento para resolver una ecuación escalar con coeficientes constantes
ay′′ + by′ + cy = 0
en el caso de que el polinomio característico tenga una raíz repetida, podría esperarse obtener una segunda solución de (9.10.5.1) multiplicando la primera solución por t. Sin embargo, esto produce y2 = tet, lo cual no funciona, ya que
mientras 
El siguiente teorema muestra qué hacer en esta situación.
Teorema 9.10.5.1
Supongamos que la matriz A de n×n tiene un valor propio λ1 de multiplicidad ≥ 2 y el espacio propio asociado tiene dimensión 1; es decir, todos los vectores propios λ1 de A son múltiplos escalares de un vector propio x. Entonces hay infinitos vectores u tales que
(A − λ1I)u = x. (9.10.5.2)
Además, si u es uno de esos vectores, entonces
y1 = xeλ1t y y2 = ueλ1t + xteλ1t (9.10.5.3)
son soluciones linealmente independientes de y′ = Ay. ♦
Una demostración completa de este teorema está más allá del alcance de este libro. La dificultad está en probar que hay un vector u que satisface (9.10.5.2), ya que det(A − λ1I) = 0. Tomaremos esto sin prueba y verificaremos las otras afirmaciones del teorema.
Ya sabemos que y1 en (9.10.5.3) es solución de y′ = Ay. Para ver que y2 también es una solución, calculamos
Como Ax = λ1x, esto se puede escribir como
y2′ − Ay2 = − ((A − λ1I)u − x)eλ1t,
y ahora (9.10.5.2) implica que y2′ = Ay2.
Para ver que y1 y y2 son linealmente independientes, suponga que c1 y c2 son constantes tales que
c1y1 + c2y2 = c1xeλ1t + c2(ueλ1t + xteλ1t) = 0. (9.10.5.4)
Debemos demostrar que c1 = c2 = 0. Multiplicando (9.10.5.4) por e−λ1t se muestra que
c1x + c2(u + xt) = 0. (9.10.5.5)
Derivando esto con respecto a t, vemos que c2x = 0, lo que implica c2 = 0, porque x ≠ 0.
Sustituyendo c2 = 0 en (9.10.5.5) se obtiene c1x = 0, lo que implica que c1 = 0, nuevamente porque x ≠ 0
Ejemplo ilustrativo 9.10.5.2
Use el Teorema 9.10.5.1 para encontrar la solución general del sistema
(9.10.5.6)
considerado en el ejemplo 9.10.5.1.
Solución:
En el Ejemplo 9.10.5.1 vimos que λ1 = 1 es un valor propio de multiplicidad 2 de la matriz de coeficientes A en (9.10.5.6), y que todos los vectores propios de A son múltiplos de
Por lo tanto
es una solución de (9.10.5.6). Del Teorema 9.10.5.1, una segunda solución viene dada por y2 = uet + xtet, donde (A − I)u = x. La matriz aumentada de este sistema es
que es equivalente por filas a
Por lo tanto las componentes de u deben satisfacer
donde u2 es arbitrario. Elegimos u2 = 0, de modo que u1 = 1/2 y
De este modo,
Dado que y1 e y2 son linealmente independientes por el Teorema 9.10.5.1, forman un conjunto fundamental de soluciones de (9.10.5.6). Por tanto, la solución general de (9.10.5.6) es
♦
Tenga en cuenta que elegir la constante arbitraria u2 para que sea distinta de cero es equivalente a sumar un múltiplo escalar de y1 a la segunda solución y2 (Ejercicio 33).
Ejemplo ilustrativo 9.10.5.3
Encuentre la solución general de
(9.10.5.7)
Solución:
El polinomio característico de la matriz de coeficientes A en (9.10.5.7) es
Por lo tanto, los valores propios son λ1 = 1 con multiplicidad 1 y λ2 = −1 con multiplicidad 2.
Los vectores propios asociados con λ1 = 1 deben satisfacer (A − I)x = 0. La matriz aumentada de este sistema es
que es equivalente por filas a
Por tanto, x1 = x3 y x2 = 2x3, donde x3 es arbitraria. Elegir x3 = 1 produce el vector propio
Por lo tanto
es una solución de (9.10.5.7).
Los vectores propios asociados con λ2 = −1 satisfacen (A + I)x = 0. La matriz aumentada de este sistema es
que es equivalente por filas a
Por tanto, x3 = 0 y x1 = −x2, donde x2 es arbitraria. Elegir x2 = 1 produce el vector propio
por lo que
es una solución de (9.10.5.7).
Dado que todos los vectores propios de A asociados con λ2 = −1 son múltiplos de x2, ahora debemos usar el Teorema 9.10.5.1 para encontrar una tercera solución de (9.10.5.7) en la forma
(9.10.5.8)
donde u es una solución de (A + I)u = x2. La matriz aumentada de este sistema es
que es equivalente por filas a
Por lo tanto, u3 = 1/2 y u1 = 1 − u2, donde u2 es arbitrario. Elegir u2 = 0 produce
y sustituyendo esto en (9.10.5.8) se obtiene la solución
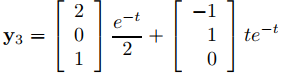
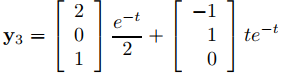
de (9.10.5.7).
Dado que el Wronskiano de {y1, y2, y3} en t = 0 es
{y1, y2, y3} es un conjunto fundamental de soluciones de (9.10.5.7). Por tanto, la solución general de (9.10.5.7) es
Teorema 9.10.5.2
Supongamos que la matriz A de n×n tiene un valor propio λ1 de multiplicidad ≥ 3 y el espacio propio asociado es unidimensional; es decir, todos los vectores propios asociados con λ1 son múltiplos escalares del vector propio x. Entonces hay infinitos vectores u tales que
(A − λ1I)u = x, (9.10.5.9)
y, si u es uno de esos vectores, hay infinitos vectores v tales que
(A − λ1I)v = u, (9.10.5.10)
Si u satisface (9.10.5.9) y v satisface (9.10.5.10), entonces
son soluciones linealmente independientes de y′ = Ay. ♦
Nuevamente, está más allá del alcance de este libro probar que hay vectores u y v que satisfacen (9.10.5.9) y (9.10.5.10). El teorema 9.10.5.1 implica que y1 e y2 son soluciones de y′ = Ay. Te dejamos el resto de la demostración (Ejercicio 34).
Ejemplo ilustrativo 9.10.5.4
Use el Teorema 9.10.5.2 para encontrar la solución general de
Solución:
El polinomio característico de la matriz de coeficientes A en (9.10.5.11) es
Por lo tanto, λ1 = 2 es un valor propio de multiplicidad 3. Los vectores propios asociados satisfacen (A − 2I)x = 0.
La matriz aumentada de este sistema es
que es equivalente por filas a
Por lo tanto, x1 = x3 y x2 = 0, por lo que los vectores propios son todos múltiplos escalares de
Por lo tanto
es una solución de (9.10.5.11).
Ahora encontramos una segunda solución de (9.10.5.11) en la forma
donde u satisface (A − 2I)u = x1. La matriz aumentada de este sistema es
que es equivalente por filas a
Haciendo u3 = 0 se obtiene u1 = −1/2 y u2 = 1/2; por eso,
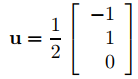
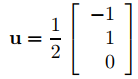
y
es una solución de (9.10.5.11).
Ahora encontramos una tercera solución de (9.10.5.11) en la forma
donde v satisface (A − 2I)v = u. La matriz aumentada de este sistema es
que es equivalente por filas a
Haciendo que v3 = 0 da como resultado v1 = 1/2 y v2 = 0; por eso,
Por lo tanto
es una solución de (9.10.5.11). Dado que y1, y2 e y3 son linealmente independientes por el Teorema 9.10.5.2, forman un conjunto fundamental de soluciones de (9.10.5.11). Por tanto, la solución general de (9.10.5.11) es
♦
Teorema 9.10.5.3
Supongamos que la matriz A de n×n tiene un valor propio λ1 de multiplicidad ≥ 3 y el espacio propio asociado es bidimensional; es decir, todos los vectores propios de A asociados con λ1 son combinaciones lineales de dos vectores propios linealmente independientes x1 y x2. Entonces hay constantes α y β (no ambas cero) tales que si
x3 = αx1 + βx2, (9.10.5.12)
entonces hay infinitos vectores u tales que
(A − λ1I)u = x3. (910.5.13)
Si u satisface (9.10.5.13), entonces
(910.5.14)
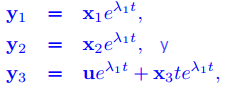
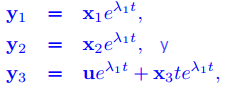
son soluciones linealmente independientes de y′ = Ay. ♦
Omitimos la demostración de este teorema.
Ejemplo ilustrativo 9.10.5.5
Use el Teorema 9.10.5.3 para encontrar la solución general de
(910.5.15)
Solución:
El polinomio característico de la matriz de coeficientes A en (9.10.5.15) es
Por lo tanto, λ1 = 1 es un valor propio de multiplicidad 3. Los vectores propios asociados satisfacen (A − I)x = 0. La matriz aumentada de este sistema es
que es equivalente por filas a
Por lo tanto, x1 = x3 y x2 es arbitrario, por lo que los vectores propios son de la forma
Por lo tanto los vectores
y 
(910.5.16)
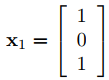
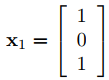
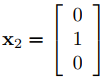
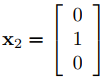
forman una base para el espacio propio, y
y 
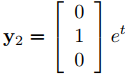
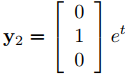
son soluciones linealmente independientes de (9.10.5.15).
Para encontrar una tercera solución linealmente independiente de (9.10.5.15), debemos encontrar las constantes α y β (no ambas cero) tales que el sistema
(A − I)u = αx1 + βx2 (9.10.5.17)
tiene una solución u. La matriz aumentada de este sistema es
que es equivalente por filas a
(9.10.5.18)
Por lo tanto (9.10.5.17) tiene solución si y solo si β = α, donde α es arbitraria. Si α = β = 1 entonces (9.10.5.12) y (10.5.16) dan
y la matriz aumentada (9.10.5.18) se convierte en
Esto implica que u1 = −1 + u3, mientras que u2 y u3 son arbitrarios. Elegir u2 = u3 = 0 produce
Por lo tanto (9.10.5.14) implica que
es una solución de (9.10.5.15). Dado que y1, y2 e y3 son linealmente independientes por el Teorema 9.10.5.3, forman un conjunto fundamental de soluciones para (9.10.5.15). Por tanto, la solución general de (9.10.5.15) es
♦
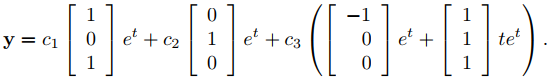
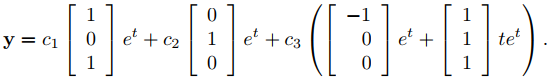
Propiedades geométricas de soluciones cuando n = 2
Ahora consideraremos las propiedades geométricas de las soluciones de un sistema de coeficientes constantes de 2 × 2
(9.10.5.19)
bajo los supuestos de esta sección; es decir, cuando la matriz
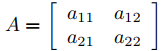
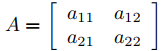
tiene un valor propio repetido λ1 y el espacio propio asociado es unidimensional. En este caso sabemos por el Teorema 9.10.5.1 que la solución general de (9.10.5.19) es
(9.10.5.20)
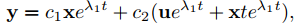
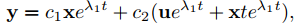
donde x es un vector propio de A y u es cualquiera de las infinitas soluciones de
(A − λ1I)u = x. (9.10.5.21)
Suponemos que λ1 ≠ 0.
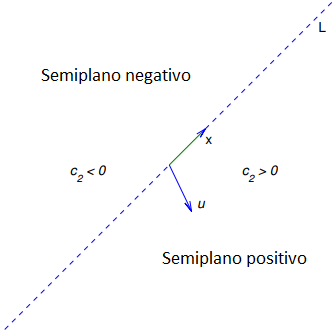
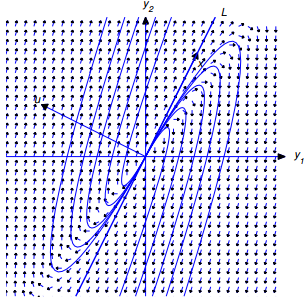
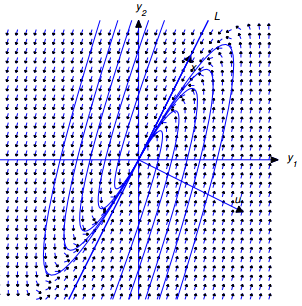
Figura 9.10.5.1 Semiplanos positivo y negativo
Sea L la recta que pasa por el origen paralela a x. Por semirecta de L nos referimos a cualquiera de los rayos obtenidos al eliminar el origen de L. (9.10.5.20) es una ecuación paramétrica de la semirrecta de L en la dirección de x si c1 > 0, o de la semirrecta de L en la dirección de −x si c1 < 0. El origen es la trayectoria de la solución trivial y ≡ 0.
En adelante, asumimos que c2 ≠ 0. En este caso, la trayectoria de (9.10.5.20) no puede intersecar a L, ya que cada punto de L está en una trayectoria obtenida al hacer c2 = 0. Por lo tanto, la trayectoria de (9.10 .5.20) debe estar completamente en uno de los semiplanos abiertos limitados por L, pero no contiene ningún punto en L. Dado que el punto inicial (y1(0), y2(0)) definido por y(0) = c1x1 + c2u está en la trayectoria, podemos determinar qué semiplano contiene la trayectoria a partir del signo de c2, como se muestra en la Figura 9.10.5.1. Por conveniencia, llamaremos semiplano positivo al semiplano donde c2 > 0. De manera similar, el semiplano donde c2 < 0 es el semiplano negativo. Debe convencerse (Ejercicio 35) de que aunque hay infinitos vectores u que satisfacen (9.10.5.21), todos definen los mismos semiplanos positivo y negativo. En las figuras, simplemente considere a u como una flecha que apunta al semiplano positivo, ya que no intentamos darle a u su longitud o dirección adecuadas en comparación con x. Para nuestros propósitos aquí, solo es importante la orientación relativa de x y u; es decir, si el semiplano positivo está a la derecha de un observador que mira en la dirección de x (como en las Figuras 9.10.5.2 y 9.10.5.5), o a la izquierda del observador (como en las Figuras 9.10.5.3 y 9.10.5.4).
|
Figura 9.10.5.2 Valor propio positivo; movimiento alejándose del origen |
Figura 9.10.5.3 Valor propio positivo; movimiento alejándose del origen |
|
Figura 9.10.5.4 Valor propio negativo; movimiento hacia el origen |
Figura 9.10.5.5 Valor propio negativo; movimiento hacia el origen |
Multiplicando (9.10.5.20) por e−λ1t se obtiene
e−λ1ty(t) = c1x + c2u + c2tx.
Dado que el último término de la derecha es dominante cuando |t| es grande, esto proporciona la siguiente información sobre la dirección de y(t):
(a) A lo largo de trayectorias en el semiplano positivo (c2 > 0), la dirección de y(t) se aproxima a la dirección de x cuando t → ∞ y a la dirección de −x cuando t → −∞.
(b) A lo largo de las trayectorias en el semiplano negativo (c2 < 0), la dirección de y(t) se aproxima a la dirección de −x cuando t → ∞ y a la dirección de x cuando t → −∞.
Desde
o
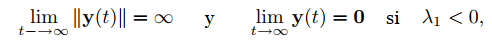
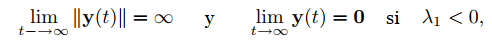
hay cuatro patrones posibles para las trayectorias de (9.10.5.19), dependiendo de los signos de c2 y λ1. Las figuras 9.10.5.2 a 9.10.5.5 ilustran estos patrones y revelan el siguiente principio:
Si λ1 y c2 tienen el mismo signo, entonces la dirección de la trayectoria se aproxima a la dirección de −x cuando ||y|| → 0 y a la dirección de x cuando ||y||| → ∞. Si λ1 y c2 tienen signos opuestos, entonces la dirección de la trayectoria se aproxima a la dirección de x cuando ||y|| → 0 y a la dirección de −x cuando ||y|| → ∞.