| 9. Ecuaciones diferenciales | 9.2 Ecuaciones diferenciales de primer orden |
9.2.6 Factores de integración
En la Sección 9.2.5 vimos que si M, N, My y Nx son continuos y My = Nx en un rectángulo abierto R entonces
M(x, y) dx + N(x, y) dy = 0 (9.2.6.1)
es exacta en R. A veces, una ecuación que no es exacta se puede hacer exacta multiplicándola por una función apropiada. Por ejemplo,
(3x + 2y2) dx + 2xy dy = 0 (9.2.6.2)
no es exacta, ya que My(x, y) = 4y ≠ Nx(x, y) = 2y en (9.2.6.2). Sin embargo, al multiplicar (9.2.6.2) por x se obtiene
(3x2 + 2xy2)dx + 2x2y dy = 0, (9.2.6.3)
lo cual es exacto, ya que My(x, y) = Nx(x, y) = 4xy en (9.2.6.3). Resolviendo (9.2.6.3) por el procedimiento dado en la Sección 9.2.5 se obtiene la solución implícita
x3 + x2y2 = c.
Una función µ = µ(x, y) es un factor integrante para (9.2.6.1) si
µ(x, y)M(x, y) dx + µ(x, y)N(x, y) dy = 0 (9.2.6.4)
es exacta. Si conocemos un factor de integración µ para (9.2.6.1), podemos resolver la ecuación exacta (9.2.6.4) por el método de la Sección 9.2.5. Sería bueno si pudiéramos decir que (9.2.6.1) y (9.2.6.4) siempre tienen las mismas soluciones, pero no es así. Por ejemplo, una solución y = y(x) de (9.2.6.4) tal que µ(x, y(x)) = 0 en algún intervalo a < x < b podría no ser una solución de (9.2.6.1) (Ejercicio 1), mientras que (9.2.6.1) puede tener una solución y = y(x) tal que µ(x, y(x)) ni siquiera está definida (Ejercicio 2). Se aplican comentarios similares si y es la variable independiente y x es la variable dependiente en (9.2.6.1) y (9.2.6.4). Sin embargo, si se define µ(x, y) distinta de cero para todo (x, y), (9.2.6.1) y (9.2.6.4) son equivalentes; es decir, tienen las mismas soluciones.
Encontrar factores de integración
Al aplicar el Teorema 9.2.5.2 (con M y N reemplazados por µM y µN), vemos que (9.2.6.4) es exacta en un rectángulo abierto R si µM, µN, (µM)y y (µN)x son continuas y
o, de manera equivalente, µyM + µMy = µxN + µNx
en R. Es mejor reescribir la última ecuación como
µ(My − Nx) = µxN − µyM, (9.2.6.5)
que se reduce al resultado conocido para ecuaciones exactas; es decir, si My = Nx entonces (9.2.6.5) se cumple con µ = 1, por lo que (9.2.6.1) es exacta.
Puede pensar que (9.2.6.5) tiene poco valor, ya que involucra derivadas parciales del factor de integración desconocido µ, y no hemos estudiado métodos para resolver tales ecuaciones. Sin embargo, ahora mostraremos que (9.2.6.5) es útil si restringimos nuestra búsqueda a factores integrantes que son productos de una función de x y una función de y; es decir, µ(x, y) = P(x)Q(y). No estamos diciendo que toda ecuación M dx + N dy = 0 tenga un factor integrante de esta forma; más bien, estamos diciendo que algunas ecuaciones tienen tales factores de integración. Ahora desarrollaremos una manera de determinar si una ecuación dada tiene tal factor de integración y un método para encontrar el factor de integración en este caso.
Si µ(x, y) = P(x)Q(y), entonces µx(x, y) = P′(x)Q(y) y µy(x, y) = P(x)Q′ (y), entonces (9.2.6.5) se convierte en
P(x)Q(y)(My − Nx) = P′(x)Q(y)N − P(x)Q′(y)M, (9.2.6.6)
o, después de dividir por P(x)Q(y),
(9.2.6.7)
Ahora deje que
entonces (9.2.6.7) se convierte en
My − Nx = p(x)N − q(y)M. (9.2.6.8)
Obtuvimos (9.2.6.8) suponiendo que M dx + N dy = 0 tiene un factor de integración µ(x, y) = P(x)Q(y). Sin embargo, ahora podemos ver (9.2.6.7) de manera diferente: si hay funciones p = p(x) y q = q(y) que satisfacen (9.2.6.8) y definimos
(9.2.6.9)
luego, al invertir los pasos que llevaron de (9.2.6.6) a (9.2.6.8) se muestra que µ(x, y) = P(x)Q(y) es un factor integrante para M dx+ N dy = 0. Al usar este Como resultado, tomamos las constantes de integración en (9.2.6.9) como cero y elegimos los signos convenientemente para que el factor de integración tenga la forma más simple.
No existe un método general simple para determinar si las funciones p = p(x) y q = q(y) que satisfacen (9.2.6.8) existen. Sin embargo, el siguiente teorema da condiciones suficientes simples para que la ecuación dada tenga un factor de integración que dependa solo de una de las variables independientes x e y, y para encontrar un factor de integración en este caso.
Teorema 9.2.6.1
Sean M, N, My y Nx continuas en un rectángulo abierto R. Entonces:
(a) Si (My − Nx)/N es independiente de y en R y definimos
entonces
(9.2.6.10)
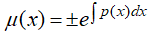
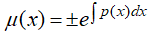
es un factor integrante de
M(x, y) dx + N(x, y) dy = 0 (9.2.6.11)
en R.
(b) Si (Nx − My)/M es independiente de x en R y definimos
entonces
(9.2.6.12)
es un factor integrante para (9.2.6.11) en R. ♦
Prueba:
(a) Si (My − Nx)/N es independiente de y, entonces (9.2.6.8) se cumple con p = (My − Nx)/N y q ≡ 0. Por lo tanto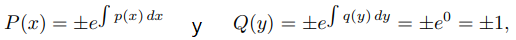
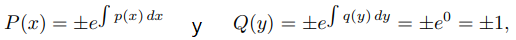
entonces (9.2.6.10) es un factor integrante para (9.2.6.11) en R.
(b) Si (Nx −My)/M es independiente de x entonces 9.2.6.8 se cumple con p ≡ 0 y q = (Nx −My)/M, y un argumento similar muestra que (9.2.6.12) es un factor integrante para (9.2.6.11) en R. ♦
Los siguientes dos ejemplos muestran cómo aplicar el Teorema 9.2.6.1.
Ejemplo ilustrativo 9.2.6.1
Encuentre un factor de integración para la ecuación
(2xy3 − 2x3y3 − 4xy2 + 2x) dx + (3x2y2 + 4y) dy = 0 (9.2.6.13)
y resuelve la ecuación.
Solución:
En (9.2.6.13)
M = 2xy3 − 2x3y3 − 4xy2 + 2x, N = 3x2y2 + 4y,
y
My − Nx = (6xy2 − 6x3y2 − 8xy) − 6xy2 = −6x3y2 − 8xy,
entonces (9.2.6.13) no es exacta. Sin embargo,
es independiente de y, por lo que el Teorema 9.2.6.1(a) se aplica con p(x) = −2x. Ya que
es un factor integrante. Multiplicando (9.2.6.13) por µ se obtiene la ecuación exacta
(9.2.6.14)
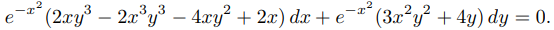
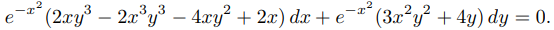
Para resolver esta ecuación, debemos encontrar una función F tal que
(9.2.6.15)
y
(9.2.6.16)
Integrando (9.2.6.16) con respecto a y se obtiene
(9.2.6.17)
Derivando esto con respecto a x se obtiene
Comparando esto con (9.2.6.15) se muestra que 
por lo tanto, podemos dejar 
en (9.2.6.17) y concluimos que
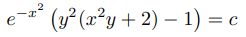
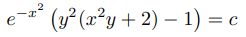
es una solución implícita de (9.2.6.14). También es una solución implícita de (9.2.6.13). ♦
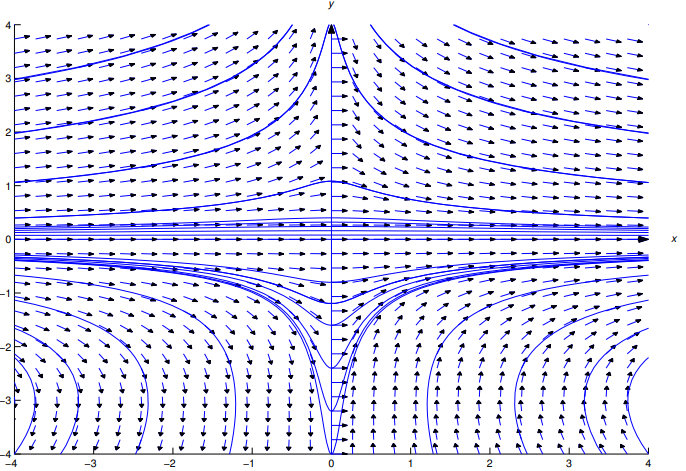
La Figura 9.2.6.1 muestra un campo direccional y algunas curvas enteras para (9.2.6.13)
Ejemplo ilustrativo 9.2.6.2
Encuentre un factor de integración para
2xy3dx + (3x2y2 + x2y3 + 1) dy = 0 (9.2.6.18)
y resuelve la ecuación.
Solución:
En (9.2.6.18),
M = 2xy3, N = 3x2y2 + x2y3 + 1,
y
My − Nx = 6xy2 − (6xy2 + 2xy3) = −2xy3,
entonces (9.2.6.18) no es exacta. Además,
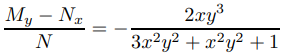
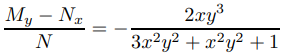
no es independiente de y, por lo que el Teorema 9.2.6.1(a) no se aplica. Sin embargo, se aplica el Teorema 2.6.1(b), ya que
es independiente de x, por lo que podemos tomar q(y) = 1. Como
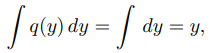
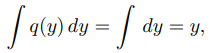
µ(y) = ey es un factor integrante. Multiplicando (9.2.6.18) por µ se obtiene la ecuación exacta
2xy3ey dx + (3x2y2 + x2y3 + 1)ey dy = 0. (9.2.6.19)
Para resolver esta ecuación, debemos encontrar una función F tal que
Fx(x, y) = 2xy3 ey (9.2.6.20)
y
Fy(x, y) = (3x2y2 + x2y3 + 1)ey. (9.2.6.21)
Integrando (9.2.6.20) con respecto a x se obtiene
F(x, y) = x2y3ey + φ(y). (9.2.6.22)
Diferenciando esto con respecto a y se obtiene
Fy = (3x2y2 + x2y3)ey + φ′(y),
y comparando esto con (9.2.6.21) muestra que φ′(y) = ey. Por lo tanto establecemos φ(y) = ey en (9.2.6.22) y concluimos que
(x2y3 + 1)ey = c
es una solución implícita de (9.2.6.19). También es una solución implícita de (9.2.6.18). La figura 9.2.6.2 muestra un campo direccional y algunas curvas integrales para (9.2.6.18). ♦
El teorema 9.2.6.1 no se aplica en el siguiente ejemplo, pero el argumento más general que condujo al teorema 9.2.6.1 proporciona un factor de integración.
Ejemplo ilustrativo 9.2.6.3
Encuentre un factor de integración para
(3xy + 6y2) dx + (2x2 + 9xy) dy = 0 (9.2.6.23)
y resuelve la ecuación
Solución:
en (9.2.6.23)
M = 33xy + 6y2, N = 2x2 + 9xy,
y
My − Nx = (3x + 12y) − (4x + 9y) = −x + 3y.
Por lo tanto
entonces el Teorema 9.2.6.1 no se aplica. Siguiendo el argumento más general que condujo al Teorema 9.2.6.1, buscamos funciones p = p(x) y q = q(y) tales que
My − Nx = p(x)N − q(y)M;
es decir
−x + 3y = p(x)(2x2 + 9xy) − q(y)(3xy + 6y2).
Dado que el lado izquierdo contiene solo términos de primer grado en x e y, reescribimos esta ecuación como
xp(x)(2x + 9y) − yq(y)(3x + 6y) = −x + 3y.
Esta será una identidad si
xp(x) = A y yq(y) = B, (9.2.6.24)
donde A y B son constantes tales que
−x + 3y = A(2x + 9y) − B(3x + 6y),
o equivalente,
−x + 3y = (2A − 3B)x + (9A − 6B)y.
Igualar los coeficientes de x e y en ambos lados muestra que la última ecuación se cumple para todo (x, y) si
que tiene la solución A = 1, B = 1. Por lo tanto (9.2.6.24) implica que
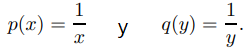
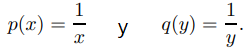
Ya que
podemos dejar que P(x) = x y Q(y) = y; por lo tanto, µ(x, y) = xy es un factor integrante. Multiplicando (9.2.6.23) por µ se obtiene la ecuación exacta
(3x2y2 + 6xy3)dx + (2x3y + 9x2y2)dy = 0.
Le dejamos a usted usar el método de la Sección 9.2.5 para mostrar que esta ecuación tiene la solución implícita
x3y2 + 3x2y3 = c. (9.2.6.25)
Esta es también una solución implícita de (9.2.6.23). Dado que x ≡ 0 y y ≡ 0 satisfacen (9.2.6.25), debe comprobar que x ≡ 0 y y ≡ 0 también son soluciones de (9.2.6.23). (¿Por qué es necesario verificar esto?)
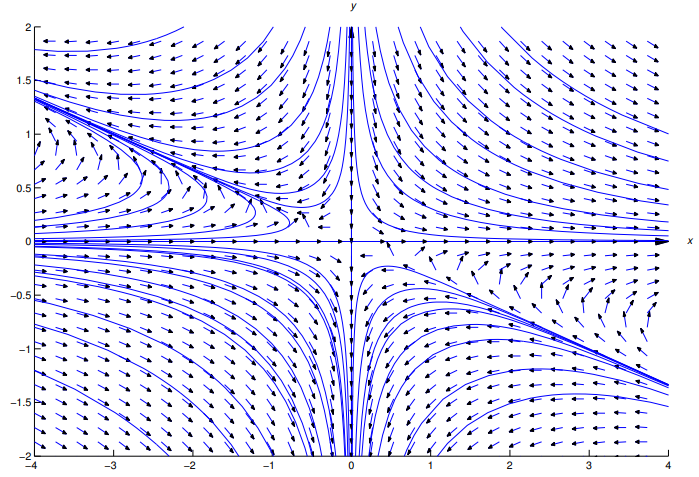
La figura 9.2.6.3 muestra un campo de direcciones y curvas integrales para (9.2.6.23). ♦
Vea el Ejercicio 28 para una discusión general de ecuaciones como (9.2.6.23).
Ejemplo ilustrativo 9.2.6.4
La ecuación separable
− y dx + (x + x6)dy = 0 (9.2.6.26)
se puede convertir a la ecuación exacta
(9.2.6.27)
multiplicando por el factor integrante
Sin embargo, para resolver (9.2.6.27) por el método de la Sección 9.2.5 tendríamos que evaluar la desagradable integral
En cambio, resolvemos (9.2.6.26) explícitamente para y encontrando un factor integrante de la forma µ(x, y) = xayb.
Solución:
En (9.2.6.26)
M = −y, N = x + x6,
y
My − Nx = −1 − (1 + 6x5) = −2 − 6x5.
Buscamos las funciones p = p(x) y q = q(y) tales que
My − Nx = p(x)N − q(y)M;
es decir,
− 2 − 6x5 = p(x)(x + x6) + q(y)y. (9.2.6.28)
El lado derecho contendrá el término −6x5 si p(x) = −6/x. Entonces (9.2.6.28) se convierte en
−2 − 6x5 = −6 − 6x5 + q(y)y,
entonces q(y) = 4/y. Ya que
y
podemos tomar P(x) = x−6 y Q(y) = y4, lo que da como resultado el factor de integración µ(x, y) = x − 6y4. Multiplicando (9.2.6.26) por µ se obtiene la ecuación exacta
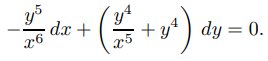
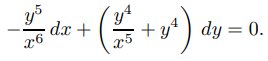
Le dejamos a usted usar el método de la Sección 9.2.5 para mostrar que esta ecuación tiene la solución implícita
Resolviendo para y obtenemos
La que reescribimos como
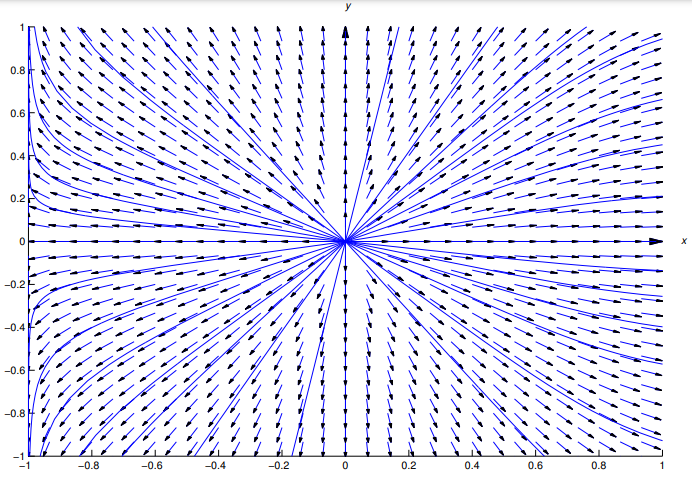
cambiando el nombre de la constante arbitraria. Esta es también una solución de (9.2.6.26).
La figura 9.2.6.4 muestra un campo de direcciones y algunas curvas integrales para (9.2.6.26). ♦