| 10. Cálculo vectorial – Vectores en el espacio | Ejercicios propuestos para el Capítulo 10.3 |

10.3 EL PRODUCTO PUNTO: Objetivos de aprendizaje

10.3.1. Calcular el producto punto (producto escalar) de dos vectores dados.
10.3.2. Determinar si dos vectores dados son perpendiculares.
10.3.3. Encontrar la dirección de los cosenos de un vector dado.
10.3.4. Explicar qué se entiende por proyección vectorial de un vector sobre otro vector y describir cómo calcularlo.
10.3.5. Calcular el trabajo realizado por una fuerza dada.

       Si aplicamos una fuerza a un objeto para que el objeto se mueva, decimos que el trabajo lo realiza la fuerza. En Introducción a las aplicaciones de la integración, observamos una fuerza constante y asumimos que la fuerza se aplicaba en la dirección del movimiento del objeto. En esas condiciones, el trabajo puede expresarse como el producto de la fuerza que actúa sobre un objeto y la distancia que se mueve el objeto. En el presente capítulo, sin embargo, hemos visto que tanto la fuerza como el movimiento de un objeto pueden representarse mediante vectores.

       En esta sección, desarrollamos una operación llamada producto punto, que nos permite calcular el trabajo en el caso en que el vector de fuerza y ​​el vector de movimiento tengan direcciones diferentes. El producto punto esencialmente nos dice cuánto del vector de fuerza se aplica en la dirección del vector de movimiento. El producto punto también puede ayudarnos a medir el ángulo formado por un par de vectores y la posición de un vector en relación con los ejes de coordenadas. Incluso proporciona una prueba simple para determinar si dos vectores se encuentran en ángulo recto.

El producto punto y sus propiedades

Ya hemos aprendido cómo sumar y restar vectores. En este capítulo, investigamos dos tipos de multiplicación de vectores. El primer tipo de multiplicación vectorial se llama producto punto, según la notación que usamos para ello, y se define de la siguiente manera:

DEFINICIÓN. Producto punto

El producto punto de los vectores u = ⟨u₁, u₂, u₃⟩ y v = ⟨v₁, v₂, v₃⟩ viene dado por la suma de los productos de los componentes

u ∙ v = u₁ v₁ + u₂ v₂ + u₃ v₃.  ♦

Tenga en cuenta que si u y v son vectores bidimensionales, calculamos su producto punto de manera similar. Por lo tanto, si u = ⟨u₁, u₂⟩ y v = ⟨v₁, v₂⟩, entonces

u ∙ v = u₁ v₁ + u₂ v₂. 

Cuando dos vectores se combinan bajo suma o resta, el resultado es un vector. Cuando dos vectores se combinan usando el producto punto, el resultado es un escalar. Por esta razón, al producto punto a menudo se llama producto escalar. También se le puede llamar el producto interno.

EJEMPLO ILUSTRATIVO 10.3_1. Cálculo de productos punto

a) Encuentre el producto escalar (punto) de u = ⟨3, 5, 2⟩ y v = ⟨− 1, 3, 0⟩.

b) Encuentre el producto escalar de p = 10i − 4j + 7k  y  q = −2i + j + 6k.

Solución:

a) Sustituya los componentes del vector en la fórmula del producto punto:

u ⋅ v = u₁ v₁ + u₂ v₂ + u₃ v₃ = 3 (−1) + 5 (3) + 2 (0) = − 3 + 15 + 0 = 12.

b) El cálculo es el mismo si los vectores se escriben usando vectores unitarios estándar. Todavía tenemos tres componentes para cada vector para sustituir en la fórmula del producto escalar:

p ⋅ q = u₁ v₁ + u₂ v₂ + u₃ v₃ = 10 (−2) + (−4) (1) + (7) (6) = −20 − 4 + 42 = 18.

Ejercicio de control 10.3_1

Encuentre u ⋅ v, donde u = ⟨2, 9, −1⟩  y  v = ⟨−3, 1, −4⟩.

       Al igual que la suma y resta de vectores, el producto punto tiene varias propiedades algebraicas. Probamos algunas de estas propiedades y dejamos el resto como ejercicios.

TEOREMA 10.3.1. Propiedades del producto punto

Sean u, v y w vectores, y c sea un escalar.

i.	u · v = v · u	Propiedad conmutativa
ii.	u · (v + w) = u · v + u · w	Propiedad distributiva
iii.	c(u · v) = (cu) · v = u · (cv)	Propiedad asociativa
iv.	v · v = ‖v‖²	Propiedad de magnitud

Prueba

Sea u = ⟨u₁, u₂, u₃⟩  y  v = ⟨v₁, v₂, v₃⟩. Luego

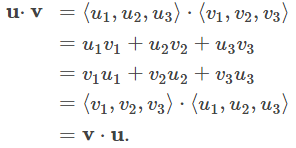
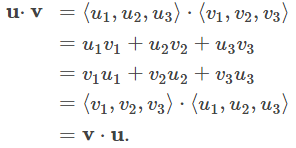
La propiedad asociativa se parece a la propiedad asociativa para la multiplicación de números reales, pero presta mucha atención a la diferencia entre los objetos escalares y vectoriales:

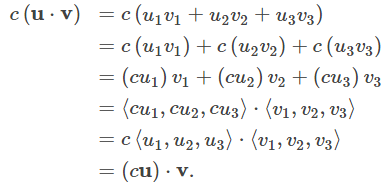
La prueba de que c (u⋅v) = u⋅ (cv) es similar.

La cuarta propiedad muestra la relación entre la magnitud de un vector y su producto punto consigo mismo:

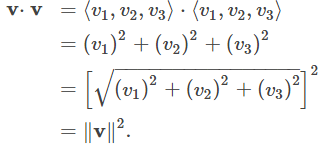
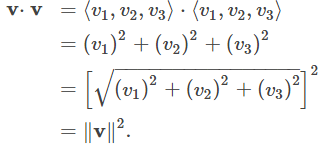
Tenga en cuenta que la definición del producto punto produce 0⋅v = 0. Por la propiedad iv., Si v⋅v = 0, entonces v = 0.

---

EJEMPLO ILUSTRATIVO 10.3_2. Uso de las  propiedades del producto punto

Sea a = ⟨1, 2, −3⟩, b = ⟨0, 2, 4⟩, y c = ⟨5, −1, 3⟩. Encuentra cada uno de los siguientes productos.
a) (a ⋅ b) c
b) a ⋅ (2c)
c) ∥b∥²

Solución:

a) Tenga presente que esta expresión pide el múltiplo escalar de c por a⋅b:

b) Esta expresión es un producto punto del vector a y el múltiplo escalar 2c:

c) Simplificar esta expresión es una aplicación directa del producto punto:

Ejercicio de control 10.3_2

Encuentre los siguientes productos para p = ⟨7, 0, 2⟩,  q = ⟨− 2, 2, −2⟩  y  r = ⟨0, 2, −3⟩.

1. (r ⋅ p) q
2. ∥p∥²

Uso del producto  punto para encontrar el ángulo entre dos vectores

Cuando dos vectores distintos de cero se colocan en posición estándar, ya sea en dos dimensiones o en tres dimensiones, forman un ángulo entre ellos (Figura 10.3_1). El producto punto proporciona una forma de encontrar la medida de este ángulo. Esta propiedad es el resultado del hecho de que podemos expresar el producto escalar en términos del coseno del ángulo formado por dos vectores.

TEOREMA 10.3.2. Evaluación de un producto punto El producto punto de dos vectores es el producto de la magnitud de cada vector y el coseno del ángulo entre ellos: u⋅v = ∥u∥∥v∥cosθ.

---

Prueba

Coloque los vectores u y v en la posición estándar y considere el vector v − u (Figura 10.3_2). Estos tres vectores forman un triángulo con longitudes laterales ∥u∥, ∥v∥ y ∥v − u∥.

(Figura 10.3_2 Las longitudes de los lados del triángulo están dadas por las magnitudes de los vectores que forman el triángulo.)

Recuerde de la trigonometría que la ley de los cosenos describe la relación entre las longitudes laterales del triángulo y el ángulo θ. La aplicación de la ley de cosenos aquí da

El producto punto proporciona una forma de reescribir el lado izquierdo de esta ecuación:

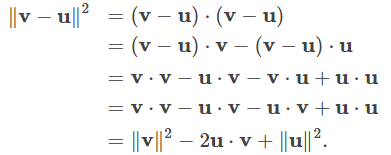
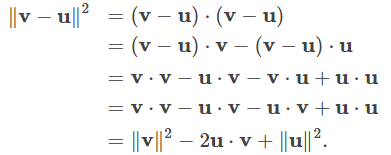
Sustituyendo en la ley del coseno para vectores, se tiene:

---

       Podemos usar esta forma del producto punto para encontrar la medida del ángulo entre dos vectores distintos de cero. La siguiente ecuación reorganiza la ecuación dada en el Teorema 10.3.2 para resolver el coseno del ángulo:

Usando esta ecuación, podemos encontrar el coseno del ángulo entre dos vectores distintos de cero. Como estamos considerando el ángulo más pequeño entre los vectores, suponemos 0° ≤ θ ≤ 180° (o 0 ≤ θ ≤ π si estamos trabajando en radianes). El coseno inverso es único en este rango, por lo que podemos determinar la medida del ángulo θ.

EJEMPLO ILUSTRATIVO 10.3_2. Encontrar el ángulo entre dos vectores

Encuentra la medida del ángulo entre cada par de vectores.
a) i + j + k  y  2i – j – 3k
b) ⟨2, 5, 6⟩  y  ⟨− 2, −4, 4⟩

Solución:

a) Para encontrar el coseno del ángulo formado por los dos vectores, sustituya las componentes de los vectores en la ecuación:

Por lo tanto,

b) Comience por encontrar el valor del coseno del ángulo entre los vectores:

Ahora, cosθ = 0 y 0 ≤ θ ≤ π, entonces θ = π / 2.

Ejercicio de control 10.3_3

Encuentra la medida del ángulo, en radianes, formado por los vectores a = ⟨1, 2, 0⟩  y  b = ⟨2, 4, 1⟩. Redondea a la centésima más cercana.