CÁLCULO DE FUNCIONES VECTORIALES; Objetivos de aprendizaje
10.9.1. Escriba una expresión para la derivada de una función vectorial.
10.9.2. Encuentre el vector tangente en un punto para un vector de posición dado.
10.9.3. Encuentre el vector tangente unitario en un punto para un vector de posición dado y explique su significado.
10.9.4. Calcule la integral definida de una función vectorial.
Para estudiar el cálculo de funciones con valores vectoriales, seguimos un camino similar al que tomamos al estudiar funciones con valores reales. Primero, definimos la derivada, luego examinamos las aplicaciones de la derivada, luego pasamos a definir integrales. Sin embargo, encontraremos algunas ideas nuevas e interesantes a lo largo del camino como resultado de la naturaleza vectorial de estas funciones y las propiedades de las curvas espaciales.
Derivadas de funciones vectoriales
Ahora que hemos visto qué es una función con valor vectorial y cómo tomar su límite, el siguiente paso es aprender a diferenciar una función con valor vectorial. La definición de la derivada de una función de valor vectorial es casi idéntica a la definición de una función de valor real de una variable. Sin embargo, debido a que el rango de una función con valor vectorial consiste en vectores, lo mismo es cierto para el rango de la derivada de una función con valor vectorial.
DEFINICIÓN. Derivada de una función de valor vectorialLa derivada de una función de valor vectorial r(t) es
siempre que exista el límite. Si r′(t) existe, entonces r es diferenciable en t. Si r′(t) existe para todas las t en un intervalo abierto (a, b), entonces r es diferenciable en el intervalo (a, b). Para que la función sea diferenciable en el intervalo cerrado [a, b], también deben existir los dos límites siguientes:
|
Muchas de las reglas para calcular derivadas de funciones con valor real se pueden aplicar también al cálculo de derivadas de funciones con valor vectorial. Recuerde que la derivada de una función de valor real puede interpretarse como la pendiente de una recta tangente o la tasa de cambio instantánea de la función. La derivada de una función de valor vectorial también puede entenderse como una tasa de cambio instantánea; por ejemplo, cuando la función representa la posición de un objeto en un punto dado en el tiempo, la derivada representa su velocidad en ese mismo punto en el tiempo.
Ahora mostramos cómo tomar la derivada de una función vectorial.
EJEMPLO ILUSTRATIVO 10.9_1. Encontrar la derivada de una función vectorial
Use la definición para calcular la derivada de la función
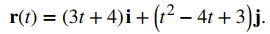
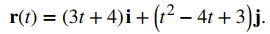
Solución:
Usemos la ecuación dada en la definición de la derivada de una función vectorial:


Observe que en los cálculos del ejemplo 10.9_1, también podríamos obtener la respuesta calculando primero la derivada de cada función componente, luego volviendo a colocar estas derivadas en la función de valor vectorial. Esto siempre es cierto para calcular la derivada de una función vectorial, ya sea en dos o tres dimensiones. Establecemos esto en el siguiente teorema. La prueba de este teorema se deriva directamente de las definiciones del límite de una función con valor vectorial y la derivada de una función con valor vectorial.
TEOREMA 10.9.2 Diferenciación de funciones vectorialesSean f, g y h funciones diferenciables de t. i. Si r(t) = f (t) i + g (t) j, entonces r ′ (t) = f ′ (t) i + g ′ (t) j. |
EJEMPLO ILUSTRATIVO 10.9_2. Cálculo de la derivada de funciones vectoriales
Utilice la diferenciación de funciones con valores vectoriales para calcular la derivada de cada una de las siguientes funciones.
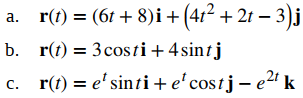
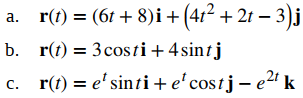
Solución:
Usamos la diferenciación de funciones con valores vectoriales y lo que sabemos sobre las funciones diferenciadoras de una variable.
a. El primer componente de r(t) = (6t + 8) i + (4t² + 2t − 3) j es f (t) = 6t + 8. El segundo componente es g (t) = 4t² + 2t − 3. Tenemos f ′(t) = 6 y g ′ (t) = 8t + 2, entonces el teorema da r′(t) = 6i + (8t + 2) j.
b. El primer componente es f (t) = 3cost y el segundo componente es g (t) = 4sent. Tenemos f ′(t) = −3sent y g ′(t) = 4cost, entonces obtenemos r′(t) = −3sent i + 4cost j.
c. El primer componente de r(t) = eᵗsent i + eᵗcost j − e²ᵗk es f (t) = eᵗsent, el segundo componente es g (t) = eᵗcost, y el tercer componente es h (t) = −e²ᵗ. Tenemos f ′ (t) = eᵗ (sent + cost), g ′ (t) = eᵗ (cost − sent) y h ′ (t) = − 2 e²ᵗ, por lo que el teorema da r ′ (t) = e²ᵗ ( sent + cost) i + eᵗ (cost − sent) j − 2 e²ᵗk.
Podemos extender a las funciones de valor vectorial las propiedades de la derivada que presentamos en la Introducción a los derivados. En particular, la regla del múltiplo constante, las reglas de suma y diferencia, la regla del producto y la regla de la cadena se extienden a las funciones de valor vectorial. Sin embargo, en el caso de la regla del producto, en realidad hay tres extensiones: (1) para una función de valor real multiplicada por una función de valor vectorial, (2) para el producto punto de dos funciones de valor vectorial, y (3 ) para el producto cruzado de dos funciones vectoriales.
TEOREMA 10.9.3 Propiedades de la derivada de funciones vectorialesSupongamos que r y u sean funciones de valores vectoriales diferenciables de t, que f sea una función de valores reales diferenciable de t, y que c sea un escalar.
|
PruebaLas pruebas de las dos primeras propiedades se deducen directamente de la definición de la derivada de una función vectorial. La tercera propiedad se puede deducir de las dos primeras propiedades, junto con la regla del producto de la Introducción a las derivadas. Sea u (t) = g (t) i + h (t) j. Luego
Para probar la propiedad iv. sea r (t) = f1 (t) i + g1 (t) j y u (t) = f2 (t) i + g2 (t) j. Luego
La prueba de la propiedad v. Es similar a la de propiedad iv. La propiedad vi. puede probarse usando la regla de la cadena. Por último, la propiedad vii. se desprende de la propiedad iv:
|
EJEMPLO ILUSTRATIVO 10.9_3. Uso de las propiedades de derivadas de funciones vectoriales
Dadas las funciones vectoriales
r (t) = (6t + 8) i + (4t ² + 2t − 3) j + 5tk
y
u (t) = (t ² − 3) i + (2t + 4) j + (t ³ − 3t) k,
calcule cada una de las siguientes derivadas utilizando las propiedades de la derivada de funciones vectoriales.
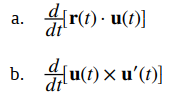
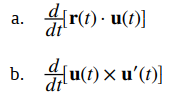
Solución:
a. Tenemos r ′ (t) = 6i + (8t + 2) j + 5k y u ′ (t) = 2t i + 2 j + (3t² – 3)k. Por lo tanto, de acuerdo con la propiedad iv .:


b. Primero, necesitamos adaptar la propiedad v. Para este problema:
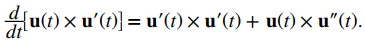
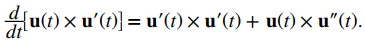
Recuerde que el producto cruz de cualquier vector consigo mismo es cero. Además, u ′ ′ (t) representa la segunda derivada de u (t):
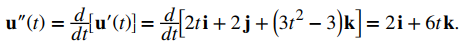
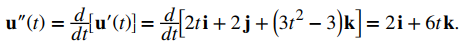
Por lo tanto,
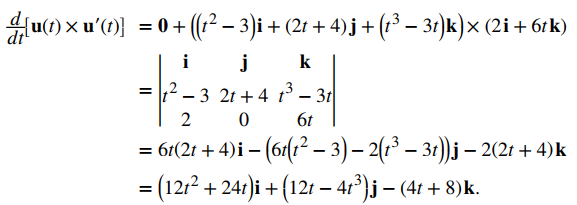
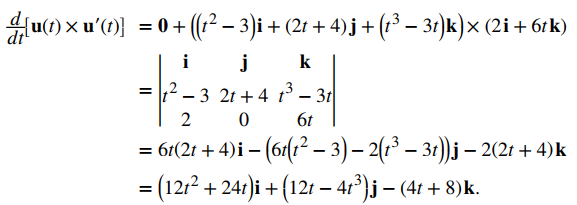

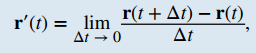
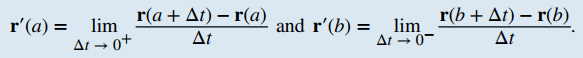


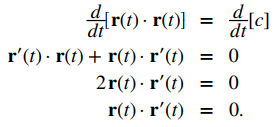
Great content! Super high-quality! Keep it up! 🙂
Ty!