| 1. Funciones y sus gráficas | Ejercicios propuestos para el Capítulo 1.4 |
1.4. Funciones inversas: Objetivos de aprendizaje
1.4.1. Determine las condiciones para que una función tenga inversa.
1.4.2. Use la prueba de línea horizontal para reconocer cuándo una función es uno a uno.
1.4.3. Encuentra la inversa de una función dada.
1.4.4. Dibuja la gráfica de una función inversa.
1.4.5. Evaluar funciones trigonométricas inversas.
Una función inversa invierte la operación realizada por una función particular. En otras palabras, haga lo que haga una función, la función inversa la deshace. En esta sección, definimos formalmente una función inversa y establecemos las condiciones necesarias para que exista una función inversa. Examinamos cómo encontrar una función inversa y estudiamos la relación entre la gráfica de una función y la gráfica de su inversa. Luego aplicamos estas ideas para definir y discutir las propiedades de las funciones trigonométricas inversas.
Existencia de una función inversa
Comenzamos con un ejemplo. Dada una función f y una salida y = f (x), a menudo nos interesa encontrar qué valor o valores de x fueron mapeados a y por f. Por ejemplo, considere la función f (x) = x³ + 4. Como cualquier salida se calcula mediante y = x³ + 4, podemos resolver esta ecuación para x para encontrar que la entrada es Esta ecuación define x como una función de y. Denotando esta función como f ⁻¹, y escribiendo
Esta ecuación define x como una función de y. Denotando esta función como f ⁻¹, y escribiendo vemos que para cualquier x en el dominio de f, f ⁻¹(f (x)) = f ⁻¹(x³ + 4) = x. Por lo tanto, esta nueva función, f ⁻¹, “deshizo” lo que hizo la función original f. Una función con esta propiedad se llama función inversa de la función original.
vemos que para cualquier x en el dominio de f, f ⁻¹(f (x)) = f ⁻¹(x³ + 4) = x. Por lo tanto, esta nueva función, f ⁻¹, “deshizo” lo que hizo la función original f. Una función con esta propiedad se llama función inversa de la función original.
DEFINICIÓN 1.4.1 Función inversa
|
Dada una función f con dominio D y rango R, su función inversa (si existe) es la función, denotada por f ⁻¹, con dominio R y rango D tal que f ⁻¹( y) = x si f (x) = y. En otras palabras, para una función f y su inversa f ⁻¹, f ⁻¹( f (x)) = x para todo x en D, y f ( f ⁻¹(y)) = y para todo y en R. |
Tenga en cuenta que f ⁻¹ se lee como “f inversa”. Aquí, el −1 no se usa como exponente y f ⁻¹(x) ≠ 1/f (x). La figura 1.4_1 muestra la relación entre el dominio y el rango de f y el dominio y el rango de f ⁻¹.
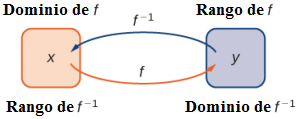
(Figura 1.4_1 Dada una función f y su inversa f ⁻¹, f ⁻¹(y) = x si y sólo si f (x) = y. El rango de f se convierte en el dominio de f ⁻¹ y el dominio de f se convierte en el rango de f ⁻¹.)
Recuerde que una función tiene exactamente una salida para cada entrada. Por lo tanto, para definir una función inversa, necesitamos asignar cada entrada a exactamente una salida. Por ejemplo, intentemos encontrar la función inversa para f (x) = x². Resolviendo la ecuación y = x² para x, llegamos a la ecuación x = ± √y. Esta ecuación no describe x como una función de y porque hay dos soluciones a esta ecuación para cada y > 0. El problema al tratar de encontrar una función inversa para f (x) = x² es que se envían dos entradas a la misma salida para cada salida y > 0. La función f (x) = x³ + 4 discutida anteriormente no tenía este problema. Para esa función, cada entrada se envió a una salida diferente. Una función que envía cada entrada a una salida diferente se denomina función uno a uno.
DEFINICIÓN 1.4.2 Función uno a uno
| Decimos que f es una función uno a uno si f (x₁) ≠ f (x₂) cuando x₁ ≠ x₂. |
Una forma de determinar si una función es uno a uno es observando su gráfica. Si una función es uno a uno, entonces no se pueden enviar dos entradas a la misma salida. Por lo tanto, si dibujamos una línea horizontal en cualquier lugar del plano xy, de acuerdo con la prueba de línea horizontal, no puede intersecar la gráfica más de una vez. Observamos que la prueba de línea horizontal es diferente de la prueba de línea vertical. La prueba de línea vertical determina si una gráfica es la gráfica de una función. La prueba de línea horizontal determina si una función es uno a uno (Figura 1.4_2).
REGLA 1.4.1: PRUEBA DE LÍNEA HORIZONTAL
| Una función f es uno a uno si y sólo si cada línea horizontal intersecta la gráfica de f no más de una vez. |
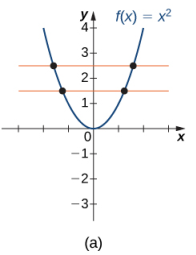
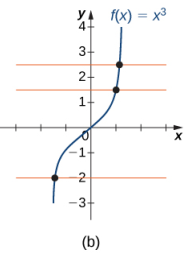
(Figura 1.4_2 (a) La función f (x) = x² no es unívoca porque falla la prueba de la línea horizontal. (b) La función f (x) = x³ es uno a uno porque pasa la prueba de la línea horizontal.)
Ejemplo ilustrativo 1.4_1 Determinar si una función es uno a uno
Para cada una de las siguientes funciones, use la prueba de línea horizontal para determinar si es uno a uno.


Solución:
a. Como la línea horizontal y = n para cualquier número entero n ≥ 0 intersecta la gráfica más de una vez, esta función no es uno a uno.
b. Dado que cada línea horizontal se cruza con la gráfica una vez (como máximo), esta función es uno a uno.
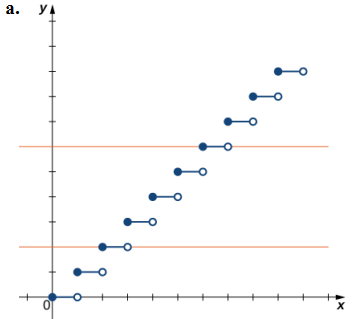
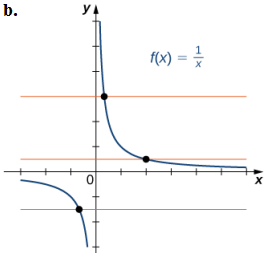
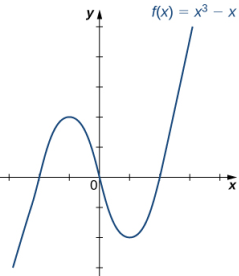
EJERCICIO DE CONTROL 1.4_1
¿La función f que está graficada en la siguiente imagen es uno a uno? Argumente su respuesta