MOVIMIENTO EN EL ESPACIO: Objetivos de aprendizaje
10.11.1. Describir los vectores de velocidad y aceleración de una partícula que se mueve en el espacio.
10.11.2. Explicar los componentes tangenciales y normales de la aceleración.
10.11.3. Declarar las leyes de Kepler del movimiento planetario.
Hemos visto cómo describir curvas en el plano y en el espacio, y cómo determinar sus propiedades, como la longitud del arco y la curvatura. Todo esto lleva al objetivo principal de este capítulo, que es la descripción del movimiento a lo largo de curvas planas y curvas espaciales. Ahora tenemos todas las herramientas que necesitamos; en esta sección, reunimos estas ideas y vemos cómo usarlas.
Vectores de movimiento en el plano y en el espacio
Nuestro punto de partida es utilizar funciones con valores vectoriales para representar la posición de un objeto en función del tiempo. Todo el material siguiente se puede aplicar a curvas en el plano o a curvas espaciales. Por ejemplo, cuando observamos la órbita de los planetas, todas las curvas que definen estas órbitas se encuentran en un plano porque son elípticas. Sin embargo, una partícula que viaja a lo largo de una hélice se mueve en una curva en tres dimensiones.
DEFINICIÓN. Vector de velocidad y vector de aceleración
Supongamos que r (t) sea una función de valor vectorial dos veces diferenciable del parámetro t que representa la posición de un objeto en función del tiempo. El vector de velocidad v(t) del objeto viene dado por
![]()
![]()
El vector de aceleración a(t) se define como
![]()
![]()
La rapidez se define para ser
![]()
![]()
Como r(t) puede estar en dos o tres dimensiones, estas funciones con valores vectoriales pueden tener dos o tres componentes. En dos dimensiones, definimos r(t) = x (t) i + y (t) j y en tres dimensiones r(t) = x (t) i + y (t) j + z (t) k. Entonces, la velocidad, la aceleración y la rapidez se pueden escribir como se muestra en la siguiente tabla.
|
EJEMPLO ILUSTRATIVO 10.11_1. Estudiar el movimiento a lo largo de una parábola
Una partícula se mueve en una trayectoria parabólica definida por la función vectorial
![]()
![]()
donde t mide el tiempo en segundos.
a. Encuentra la velocidad, aceleración y rapidez como funciones del tiempo.
b. Dibuje la curva junto con el vector de velocidad en el tiempo t = 1.
Solución:
a. Utilizamos las ecuaciones respectivas de velocidad, aceleración y rapidez:


La gráfica de


es una porción de una parábola (figura 10.11_1). El vector de velocidad en t = 1 es


y el vector de aceleración en t = 1 es


Observe que el vector de velocidad es tangente a la ruta, como siempre es el caso.


Para obtener una mejor comprensión de los vectores de velocidad y aceleración, imagine que conduce por una carretera con curvas. Si no gira el volante, continuaría en línea recta y saldría de la carretera. La rapidez a la que viaja cuando sale de la carretera, junto con la dirección, proporciona un vector que representa su velocidad, como se ilustra en la siguiente figura.


Sin embargo, el hecho de que debe girar el volante para permanecer en el camino indica que su velocidad siempre está cambiando (incluso si su rapidez no lo está) porque su dirección cambia constantemente para mantenerse en el camino. A medida que gira a la derecha, su vector de aceleración también apunta a la derecha. A medida que gira hacia la izquierda, su vector de aceleración apunta hacia la izquierda. Esto indica que sus vectores de velocidad y aceleración cambian constantemente, independientemente de si su rapidez real varía (Figura 10.11_3).


Componentes del vector de aceleración
Podemos combinar algunos de los conceptos discutidos en Longitud de arco y Curvatura con el vector de aceleración para obtener una comprensión más profunda de cómo este vector se relaciona con el movimiento en el plano y en el espacio. Recuerde que la unidad de vector tangente T y la unidad de vector normal N forman un plano osculador en cualquier punto P en la curva definida por una función de valor vectorial r(t). El siguiente teorema muestra que el vector de aceleración a(t) se encuentra en el plano osculador y puede escribirse como una combinación lineal de la unidad de tangente y los vectores unitarios normales.
TEOREMA 10.11.1 El plano del vector de aceleraciónEl vector de aceleración a(t) de un objeto que se mueve a lo largo de una curva trazada por una función doblemente diferenciable r(t) se encuentra en el plano formado por el vector unitario tangente T(t) y el vector normal unitario principal N(t) a C. Además,
Aquí, v(t) es la velocidad del objeto y κ es la curvatura de C trazada por r(t). |
PruebaDebido a que v(t) = r ′(t) y T (t) = r ′ (t) / ∥ r ′(t) ∥, tenemos v(t) = ∥ r ′(t) ∥T(t) = v(t) T(t). Ahora diferenciamos esta ecuación:
Como N (t) = T ′ (t) ∥T ′ (t) ∥, sabemos que T ′ (t) = ∥T ′ (t) ∥N (t), entonces
Una fórmula para la curvatura es
entonces
Esto da
|
Los coeficientes de T(t) y N(t) se denominan componente tangencial de la aceleración y componente normal de la aceleración, respectivamente. Escribimos aT para denotar el componente tangencial y aN para denotar el componente normal.
TEOREMA 10.11_2 Componentes tangenciales y normales de la aceleraciónSea r(t) una función de valor vectorial que denota la posición de un objeto en función del tiempo. Entonces a(t) = r′ ′(t) es el vector de aceleración. Los componentes tangenciales y normales de la aceleración aT y aN están dados por las fórmulas
y
Estos componentes están relacionados por la fórmula
Aquí T(t) es el vector tangente unitario de la curva definida por r(t), y N(t) es el vector normal unitario de la curva definida por r(t). |
El componente normal de la aceleración también se denomina componente centrípeto de la aceleración o, a veces, componente radial de la aceleración. Para comprender la aceleración centrípeta, suponga que viaja en un automóvil en una pista circular a una velocidad constante. Luego, como vimos anteriormente, el vector de aceleración apunta hacia el centro de la pista en todo momento. Como conductor del automóvil, siente un tirón hacia el exterior de la pista porque está girando constantemente. Esta sensación actúa en la dirección opuesta de la aceleración centrípeta. Lo mismo es válido para los caminos no circulares. La razón es que su cuerpo tiende a viajar en línea recta y resiste la fuerza resultante de la aceleración que lo empuja hacia un lado. Tenga en cuenta que en el punto B de la figura 10.11_4, el vector de aceleración apunta hacia atrás. Esto se debe a que el automóvil está desacelerando a medida que avanza en la curva.


Los vectores unitarios tangenciales y normales en cualquier punto dado de la curva proporcionan un marco de referencia en ese punto. Los componentes tangenciales y normales de la aceleración son las proyecciones del vector de aceleración en T y N, respectivamente.
EJEMPLO ILUSTRATIVO 10.11_2. Encontrar componentes de aceleración
Una partícula se mueve en una ruta definida por la función vectorial


dónde t mide el tiempo en segundos y la distancia se mide en pies.
a. Encuentre aT y aN como funciones de t.
b. Encuentre aT y aN en el tiempo t = 2.
Solución:
a. Comencemos con la ecuación del componente tangencial de la aceleración:


Luego aplicamos la ecuación del componente normal de la aceleración:


b. Debemos evaluar cada una de las respuestas de la parte a. en t = 2:


Las unidades de aceleración son pies por segundo al cuadrado, al igual que las unidades de los componentes normales y tangenciales de la aceleración.
Movimiento de proyectiles
Ahora veamos una aplicación de funciones vectoriales. En particular, consideremos el efecto de la gravedad en el movimiento de un objeto a medida que viaja por el aire y cómo determina la trayectoria resultante de ese objeto. A continuación, ignoramos el efecto de la resistencia del aire. Esta situación, con un objeto que se mueve con una velocidad inicial pero sin fuerzas que actúen sobre él aparte de la gravedad, se conoce como movimiento de proyectil. Describe el movimiento de objetos desde pelotas de golf hasta pelotas de béisbol y desde flechas hasta balas de cañón.
Primero tenemos que elegir un sistema de coordenadas. Si estamos parados en el origen de este sistema de coordenadas, entonces elegimos que el eje y positivo esté hacia arriba, el eje y negativo esté hacia abajo y el eje x positivo esté hacia adelante (es decir, lejos del lanzador de el objeto). El efecto de la gravedad es hacia abajo, por lo que la segunda ley de Newton nos dice que la fuerza sobre el objeto resultante de la gravedad es igual a la masa del objeto multiplicada por la aceleración resultante de la gravedad, o Fg = mg, donde Fg representa la fuerza de la gravedad y g representa la aceleración resultante de la gravedad en la superficie de la Tierra. El valor de g en el sistema de medición inglés es de aproximadamente 32 pies / seg² y es de aproximadamente 9.8 m / seg² en el sistema métrico. Esta es la única fuerza que actúa sobre el objeto. Como la gravedad actúa en dirección descendente, podemos escribir la fuerza resultante de la gravedad en la forma Fg = −mg j, como se muestra en la siguiente figura.


La segunda ley de Newton también nos dice que F = ma, donde a representa el vector de aceleración del objeto. Esta fuerza debe ser igual a la fuerza de la gravedad en todo momento, por lo que sabemos que


Ahora usamos el hecho de que el vector de aceleración es la primera derivada del vector de velocidad. Por lo tanto, podemos reescribir la última ecuación en la forma


Al tomar la antiderivada de cada lado de esta ecuación obtenemos


para algún vector constante C₁. Para determinar el valor de este vector, podemos usar la velocidad del objeto en un tiempo fijo, digamos en el tiempo t = 0. Llamamos a esta velocidad la velocidad inicial: v(0) = v₀. Por lo tanto, v(0) = – g (0) j + C₁ = v₀ y C₁ = v₀. Esto da el vector de velocidad como v(t) = – gt j + v₀.
A continuación, usamos el hecho de que la velocidad v(t) es la derivada de la posición s(t). Esto da la ecuación
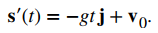
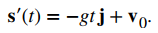
Tomar la antiderivada de ambos lados de esta ecuación conduce a


con otro vector constante desconocido C₂. Para determinar el valor de C₂, podemos usar la posición del objeto en un momento dado, digamos en el tiempo t = 0. Llamamos a esta posición la posición inicial: s(0) = s₀. Por lo tanto, s(0) = – (1/2) g (0)² j + v₀ (0) + C₂ = s₀ y C₂ = s₀. Esto proporciona la posición del objeto en cualquier momento como


Echemos un vistazo más de cerca a la velocidad inicial y la posición inicial. En particular, suponga que el objeto se lanza hacia arriba desde el origen en un ángulo θ a la horizontal, con una velocidad inicial v₀. ¿Cómo podemos modificar el resultado anterior para reflejar este escenario? Primero, podemos suponer que se arroja desde el origen. Si no, entonces podemos mover el origen al punto desde donde se arroja. Por lo tanto, s₀ = 0, como se muestra en la siguiente figura.


Podemos reescribir el vector de velocidad inicial en la forma v₀ = v₀ cosθ i + v₀senθ j. Entonces la ecuación para la función de posición s(t) se convierte en


El coeficiente de i representa la componente horizontal de s(t) y es la distancia horizontal del objeto desde el origen en el tiempo t. El valor máximo de la distancia horizontal (medido a la misma altitud inicial y final) se denomina rango R. El coeficiente de j representa la componente vertical de s(t) y es la altitud del objeto en el tiempo t. El valor máximo de la distancia vertical es la altura H.
EJEMPLO ILUSTRATIVO 10.11_3. Movimiento de una bala de cañón
Durante la celebración del Día de la Independencia, se dispara una bala de cañón desde un cañón en un acantilado hacia el agua. El cañón apunta a un ángulo de 30 ° sobre la horizontal y la velocidad inicial de la bala de cañón es de 600 pies / seg. El acantilado está a 100 pies sobre el agua (Figura 10.11_7).
a. Encuentra la altura máxima de la bala de cañón.
b. ¿Cuánto tiempo tardará la bala de cañón en salpicar el mar?
c. ¿A qué distancia del mar llegará la bala de cañón al agua?


Solución:
Usamos la ecuación


con θ = 30 °, g = 32 pies / seg², y v₀ = 600 pies / seg. Entonces la ecuación de posición se convierte en


a. La bala de cañón alcanza su altura máxima cuando el componente vertical de su velocidad es cero, porque la bala de cañón no sube ni baja en ese punto. El vector de velocidad es


Por lo tanto, la componente vertical de la velocidad viene dada por la expresión 300 − 32t. Establecer esta expresión igual a cero y resolver para t da t = 9.375 segundos. La altura de la bala de cañón en este momento viene dada por el componente vertical del vector de posición, evaluado en t = 9.375.


Por lo tanto, la altura máxima de la bala de cañón es 1406.39 pies sobre el cañón, o 1506.39 pies sobre el nivel del mar.
b. Cuando la bala de cañón cae en el agua, está a 100 pies debajo del cañón. Por lo tanto, la componente vertical del vector de posición es igual a −100. Al establecer la componente vertical de s(t) igual a −100 y resolver, obtenemos


El valor positivo de t que resuelve esta ecuación es aproximadamente 19.08. Por lo tanto, la bala de cañón golpea el agua después de aproximadamente 19.08 segundos.
c. Para encontrar la distancia al mar, simplemente sustituimos la respuesta de la parte (b) en s(t):


Por lo tanto, la pelota golpea el agua aproximadamente a 9914.26 pies de distancia de la base del acantilado. Observe que la componente vertical del vector de posición está muy cerca de −100, lo que nos dice que la pelota acaba de golpear el agua. Tenga en cuenta que 9914.26 pies no es el alcance real del cañón ya que la bala de cañón aterriza en el océano en una ubicación debajo del cañón. El alcance del cañón se determinaría al encontrar qué tan lejos está la bala de cañón cuando su altura es de 100 pies sobre el agua (lo mismo que la altitud del cañón).
Queda una última pregunta: en general, ¿cuál es la distancia máxima que puede recorrer un proyectil, dada su velocidad inicial? Para determinar esta distancia, asumimos que el proyectil se dispara desde el nivel del suelo y deseamos que regrese al nivel del suelo. En otras palabras, queremos determinar una ecuación para el rango. En este caso, la ecuación de movimiento de proyectil es


Establecer el segundo componente igual a cero y resolver t produce


Por lo tanto, cualquiera


Estamos interesados en el segundo valor de t, por lo que lo sustituimos en s(t), queda


Por lo tanto, la expresión para el alcance de un proyectil disparado en un ángulo θ es


La única variable en esta expresión es θ. Para maximizar la distancia recorrida, tome la derivada del coeficiente de i con respecto a θ y póngalo igual a cero:


Este valor de θ es el valor positivo más pequeño que hace que la derivada sea igual a cero. Por lo tanto, en ausencia de resistencia al aire, el mejor ángulo para disparar un proyectil (para maximizar el alcance) está en un ángulo de 45 °. La distancia que viaja viene dada por


Por lo tanto, el rango para un ángulo de


Leyes de Kepler
A principios del siglo XVII, Johannes Kepler pudo utilizar los datos sorprendentemente precisos de su mentor Tycho Brahe para formular sus tres leyes de movimiento planetario, ahora conocidas como las leyes de movimiento planetario de Kepler. Estas leyes también se aplican a otros objetos en el sistema solar en órbita alrededor del Sol, como los cometas (por ejemplo, el cometa Halley) y los asteroides. Las variaciones de estas leyes se aplican a los satélites en órbita alrededor de la Tierra.
TEOREMA 10.11.3 Leyes de KeplerLas tres leyes del movimiento planetario de Kepler son: |


La tercera ley de Kepler es especialmente útil cuando se usan unidades apropiadas. En particular, 1 unidad astronómica se define como la distancia promedio de la Tierra al Sol, y ahora se reconoce que es 149,597,870,700 m o, aproximadamente 93,000,000 millas. Por lo tanto, escribimos 1 A.U. = 93,000,000 mi. Dado que el tiempo que tarda la Tierra en orbitar al Sol es de 1 año, utilizamos los años terrestres por unidades de tiempo. Luego, sustituyendo 1 año por el período de la Tierra y 1 A.U. para la distancia promedio al Sol, la tercera ley de Kepler se puede escribir como


para cualquier planeta en el sistema solar, donde Tp es el período de ese planeta medido en años terrestres y Dp es la distancia promedio de ese planeta al Sol medido en unidades astronómicas. Por lo tanto, si conocemos la distancia promedio de un planeta al Sol (en unidades astronómicas), podemos calcular la duración de su año (en años terrestres) y viceversa.
Las leyes de Kepler fueron formuladas en base a observaciones de Brahe; sin embargo, no se probaron formalmente hasta que Sir Isaac Newton pudo aplicar el cálculo. Además, Newton pudo generalizar la tercera ley de Kepler a otros sistemas orbitales, como una luna que orbita alrededor de un planeta. La tercera ley original de Kepler sólo se aplica a los objetos que orbitan alrededor del Sol.
PruebaProbemos ahora la primera ley de Kepler usando el cálculo de funciones vectoriales. Primero necesitamos un sistema de coordenadas. Coloquemos el Sol en el origen del sistema de coordenadas y dejemos que la función de valor vectorial r(t) represente la ubicación de un planeta en función del tiempo. Newton probó la ley de Kepler usando su segunda ley de movimiento y su ley de gravitación universal. La segunda ley de movimiento de Newton se puede escribir como F = ma, donde F representa la fuerza neta que actúa en el planeta. Su ley de gravitación universal se puede escribir en la forma
lo que indica que la fuerza resultante de la atracción gravitacional del Sol apunta hacia el Sol y tiene magnitud
Figura 10.11_9 La fuerza gravitacional entre la Tierra y el Sol es igual a la masa de la tierra multiplicada por su aceleración. Al establecer estas dos fuerzas iguales entre sí, y utilizando el hecho de que a(t) = v′(t), obtenemos
que puede reescribirse como
Esta ecuación muestra que los vectores dv / dt y r son paralelos entre sí, por lo que dv / dt × r = 0. A continuación, diferenciemos r × v con respecto al tiempo:
Esto demuestra que r × v es un vector constante, que llamamos C. Dado que r y v son perpendiculares a C para todos los valores de t, deben estar en un plano perpendicular a C. Por lo tanto, el movimiento del planeta se encuentra en un plano. A continuación calculamos la expresión dv / dt × C:
La última igualdad en la ecuación anterior proviene de la fórmula del producto cruz triple (Introducción a los vectores en el espacio). Necesitamos una expresión para r⋅v. Para calcular esto, diferenciamos r⋅r con respecto al tiempo:
Como r⋅r = ∥r∥², también tenemos
Combinando las dos últimas ecuaciones, obtenemos
Al sustituir esto último en la ecuación
nos da
Sin embargo,
Por lo tanto, la ecuación
se convierte en
Como C es un vector constante, podemos integrar ambos lados y obtener
donde D es un vector constante. Nuestro objetivo es resolver por ∥r∥. Comencemos calculando r⋅ (v × C):
Sin embargo, r⋅ (v × C) = (r × v) ⋅C, entonces
Como r × v = C, tenemos
Tenga en cuenta que r⋅D = ∥r∥∥D∥cosθ, donde θ es el ángulo entre r y D. Por lo tanto,
Resolviendo para ∥r∥,
donde e = ∥D∥ / GM. Esta es la ecuación polar de una cónica con un foco en el origen, que configuramos para ser el Sol. Es una hipérbola si e > 1, una parábola si e = 1, o una elipse si e < 1. Como los planetas tienen órbitas cerradas, la única posibilidad es una elipse. Sin embargo, en este punto debe mencionarse que los cometas hiperbólicos existen. Estos son objetos que simplemente pasan a través del sistema solar a velocidades demasiado grandes para quedar atrapados en una órbita alrededor del Sol. A medida que pasan lo suficientemente cerca del Sol, el campo gravitacional del Sol desvía la trayectoria lo suficiente como para que el camino se vuelva hiperbólico. |
EJEMPLO ILUSTRATIVO 10.11_4. Uso de la tercera ley de Kepler para órbitas no heliocéntricas
La tercera ley de Kepler del movimiento planetario puede modificarse para el caso de un objeto en órbita alrededor de un objeto que no sea el Sol, como la Luna alrededor de la Tierra. En este caso, la tercera ley de Kepler se convierte en


donde m es la masa de la Luna y M es la masa de la Tierra, a representa la longitud del eje mayor de la órbita elíptica y P representa el período.
Dado que la masa de la Luna es 7.35 × 10²² kg, la masa de la Tierra es 5.97 × 10²⁴ kg, G = 6.67 × 10⎺¹¹ m³ / kg⋅seg², y el período de la luna es 27.3 días, encontremos la longitud del mayor Eje de la órbita de la Luna alrededor de la Tierra.
Solución:
Es importante ser coherente con las unidades. Dado que la constante gravitacional universal contiene segundos en las unidades, también necesitamos usar segundos para el período de la Luna:


Sustituya todos los datos en la ecuación anterior y resuelva para a:


Dato
Según solarsystem.nasa.gov, la distancia promedio real de la Luna a la Tierra es de 384,400 km. Esto se calcula utilizando reflectores dejados en la Luna por los astronautas del Apolo en la década de 1960.
EJEMPLO ILUSTRATIVO 10.11_5. El cometa Halley


Ahora volvemos al primer capítulo, que analiza el movimiento del cometa Halley alrededor del Sol. La primera ley de Kepler establece que el cometa Halley sigue un camino elíptico alrededor del Sol, con el Sol como foco de la elipse. El período del cometa Halley es de aproximadamente 76,1 años, dependiendo de qué tan cerca pase Júpiter y Saturno a medida que pasa a través del sistema solar exterior. Usemos T = 76.1 años. ¿Cuál es la distancia promedio del cometa Halley del Sol?
Solución:
Usando la ecuación T2 = D3 con T = 76.1, obtenemos D³ = 5791.21, entonces D ≈ 17.96 U. A. Esto llega a aproximadamente 1.67 × 10⁹ mi.
Una pregunta natural es: ¿Cuáles son las distancias máximas (afelio) y mínimas (perihelio) del cometa Halley al sol? La excentricidad de la órbita del cometa Halley es 0.967 (Fuente: http://nssdc.gsfc.nasa.gov/planetary/factsheet/cometfact.html). Recuerde que la fórmula para la excentricidad de una elipse es e = c / a, donde a es la longitud del semieje mayor y c es la distancia desde el centro a cualquier foco. Por lo tanto, 0.967 = c / 17.96 y c ≈ 17.37 U.A. Restando esto de a da la distancia del perihelio p = a − c = 17.96 − 17.37 = 0.59 U. A. Según el Centro Nacional de Datos de Ciencia Espacial (Fuente: http://nssdc.gsfc.nasa.gov/planetary/factsheet/cometfact.html), la distancia del perihelio para el cometa Halley es de 0.587 U. A. Para calcular la distancia del afelio, agregamos


Esto es aproximadamente 3.3 × 10⁹ mi. La distancia promedio de Plutón al Sol es de 39.5 A.U. (Fuente: http://www.oarval.org/furthest.htm), por lo que parece que el cometa Halley se mantiene justo dentro de la órbita de Plutón.













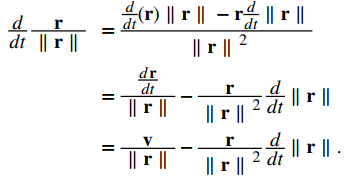




Muchas gracias por la información. Gran aporte de esta web. Reciba un cordial saludo!
Gracias, bienvenida! 😺
¡Es como si leyeras mi mente, es exactamente como deseaba que me explicaran el tema ! Parece que sabes mucho sobre esto, como si hubieras escrito el libro o algo así. Este es un gran sitio web. Un gran aporte. Definitivamente regresaré.