| 5. La integral y Técnicas de integración | Ejercicios propuestos para el Capítulo 5.4 |
5.4 Fórmulas de integración y el teorema del cambio neto
Objetivos de aprendizaje:
5.4.1. Aplicar las fórmulas básicas de integración.
5.4.2. Explicar la importancia del teorema del cambio neto.
5.4.3. Usa el teorema del cambio neto para resolver problemas aplicados.
5.4.4. Aplica las integrales de funciones pares e impares.
En esta sección, usamos algunas fórmulas de integración básicas necesarias para resolver algunos problemas de aplicación elementales. Es importante tener en cuenta que estas fórmulas se presentan en términos de integrales indefinidas. Aunque las integrales definidas e indefinidas están estrechamente relacionadas, hay algunas diferencias clave a tener en cuenta. Una integral definida es un número (cuando los límites de integración son constantes) o una sola función (cuando uno o ambos límites de integración son variables). Una integral indefinida representa una familia de funciones, todas las cuales difieren en una constante. A medida que se familiarice con la integración, tendrá una idea de cuándo usar integrales definidas y cuándo usar integrales indefinidas. Naturalmente, seleccionará el enfoque correcto para un problema determinado sin pensar demasiado en ello. Sin embargo, hasta que estos conceptos se consoliden en su mente, piense detenidamente si necesita una integral definida o una integral indefinida y asegúrese de utilizar la notación adecuada según su elección.
Fórmulas básicas de integración
Recuerde las fórmulas de integración dadas en la tabla en Antiderivadas y la regla sobre las propiedades de integrales definidas. Veamos algunos ejemplos de cómo aplicar estas reglas.
EJEMPLO ILUSTRATIVO 5.4_1. Integrando una Función Usando la Regla de la Potencia
Use la regla de la potencia para integrar la función
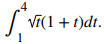
Solución:
El primer paso es reescribir la función y simplificarla para que podamos aplicar la regla de potencia:
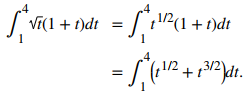
Ahora aplique la regla de la potencia:
 ♦
♦
Ejercicio de control 5.4.1
Encuentra la integral definida de \( f(x) = x^2 – 3x \) sobre el intervalo \( [1, 3] \). ♦
El teorema del cambio neto
El teorema del cambio neto considera la integral de una tasa de cambio. Dice que cuando una cantidad cambia, el nuevo valor es igual al valor inicial más la integral de la tasa de cambio de esa cantidad. La fórmula se puede expresar de dos maneras. La segunda es más familiar; es simplemente la integral definida.
TEOREMA 5.4.1. Teorema del cambio neto
El nuevo valor de una cantidad cambiante es igual al valor inicial más la integral de la tasa de cambio:
\[ F(b) = F(a) + \int_{a}^{b} F'(x) \, dx \]o
\[ \int_{a}^{b} F'(x) \, dx = F(b) – F(a). \]♦
Restando F(a) de ambos lados de la primera ecuación se obtiene la segunda ecuación. Dado que son fórmulas equivalentes, cuál usamos depende de la aplicación.
La importancia del teorema del cambio neto radica en los resultados. El cambio neto se puede aplicar al área, la distancia y el volumen, por nombrar solo algunas aplicaciones. El cambio neto representa las cantidades negativas automáticamente sin tener que escribir más de una integral. Para ilustrar, apliquemos el teorema del cambio neto a una función de velocidad en la que el resultado es el desplazamiento.
Observamos un ejemplo simple de esto en La Integral Definida. Supongamos que un automóvil se mueve hacia el norte (la dirección positiva) a 40 mph entre las 2 p.m. y a las 4 p.m., luego el automóvil se mueve hacia el sur a 30 mph entre las 4 p.m. y 5 p.m. Podemos graficar este movimiento como se muestra en la Figura 5.4_1.

Figura 5.4_1 El gráfico muestra la velocidad versus el tiempo para el movimiento dado de un automóvil.
Tal como lo hicimos antes, podemos usar integrales definidas para calcular el desplazamiento neto y la distancia total recorrida. El desplazamiento neto viene dado por
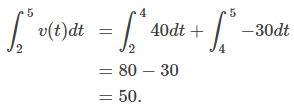
Así, a las 5 p.m. el auto está a 50 millas al norte de su posición inicial. La distancia total recorrida viene dada por
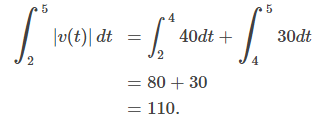
Por lo tanto, entre las 2 p.m. y a las 5 p.m., el automóvil viajó un total de 110 millas.
Para resumir, el desplazamiento neto puede incluir valores positivos y negativos. En otras palabras, la integral de la función de velocidad representa la distancia hacia adelante y la distancia hacia atrás. Para encontrar el desplazamiento neto, integre la función de velocidad en el intervalo. La distancia total recorrida, por otro lado, siempre es positiva. Para encontrar la distancia total recorrida por un objeto, independientemente de la dirección, necesitamos integrar el valor absoluto de la función de velocidad.
EJEMPLO ILUSTRATIVO 5.4_2. Encontrar el desplazamiento neto
Dada la función de velocidad v(t) = 3t − 5 (en metros por segundo) para una partícula en movimiento desde el tiempo t = 0 hasta el tiempo t = 3, encuentre el desplazamiento neto de la partícula.
Solución:
Aplicando el teorema del cambio neto, tenemos
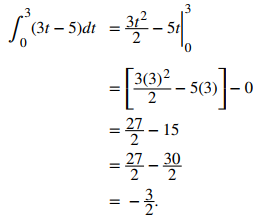
El desplazamiento neto es −32 m (Figura 5.4_2).
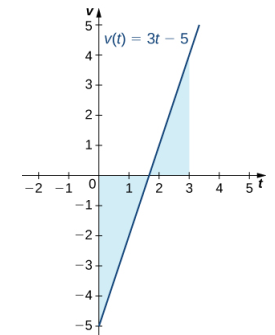
Figura 5.4_2 La gráfica muestra la velocidad frente al tiempo para una partícula que se mueve con una función de velocidad lineal. ♦
EJEMPLO ILUSTRATIVO 5.4_3. Encontrar la distancia total recorrida
Use el ejemplo 5.4_2 para encontrar la distancia total recorrida por una partícula de acuerdo con la función de velocidad v (t) = 3t − 5 m/seg durante un intervalo de tiempo [0, 3].
Solución:
La distancia total recorrida incluye los valores positivos y negativos. Por lo tanto, debemos integrar el valor absoluto de la función de velocidad para encontrar la distancia total recorrida.
Para continuar con el ejemplo, use dos integrales para encontrar la distancia total. Primero, encuentre la intersección t de la función, ya que allí es donde ocurre la división del intervalo. Establezca la ecuación igual a cero y resuelva para t. Así,
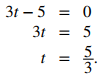
Los dos subintervalos son [0, 5/3] y [5/3, 3]. Para encontrar la distancia total recorrida, integre el valor absoluto de la función. Como la función es negativa en el intervalo [0, 5/3], tenemos |v(t)| = −v(t) durante ese intervalo. Sobre [5/3, 3], la función es positiva, entonces |v(t)| = v(t). Por lo tanto, tenemos
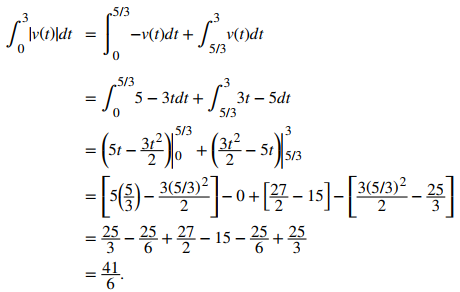
Entonces, la distancia total recorrida es de 146 m. ♦
Ejercicio de control 5.4.2
Encuentra el desplazamiento neto y la distancia total recorrida en metros, dada la función de velocidad \( f(t) = \frac{1}{2}e^t – 2 \) en el intervalo \( [0, 2] \). ♦
Aplicando el teorema del cambio neto
El teorema del cambio neto se puede aplicar al flujo y consumo de fluidos, como se muestra en el ejemplo 5.4_4.
EJEMPLO ILUSTRATIVO 5.4_4. ¿Cuántos galones de gasolina se consumen?
Si el motor de una lancha se arranca en t = 0 y la embarcación consume gasolina a 5 − t³ galones / hora durante la primera hora, ¿cuánta gasolina se usa en las primeras 2 horas?
Solución:
Exprese el problema como una integral definida, integre y evalúe utilizando el Teorema fundamental del cálculo. Los límites de integración son los puntos finales del intervalo [0, 2]. Tenemos

Por lo tanto, la lancha utiliza 6 galones de gas en 2 horas. ♦
EJEMPLO ILUSTRATIVO 5.4_5. Barcos de hielo

Como vimos al comienzo del capítulo, los mejores corredores de botes de hielo (Figura 5.4_3) pueden alcanzar velocidades de hasta cinco veces la velocidad del viento. Sin embargo, Andrew es un navegante de hielo intermedio, por lo que alcanza velocidades iguales a solo el doble de la velocidad del viento. Supongamos que Andrew saca su bote de hielo una mañana cuando una brisa suave de 5 mph ha soplado toda la mañana. Sin embargo, cuando Andrew prepara su bote de hielo, el viento comienza a levantarse. Durante su primera media hora de navegación en hielo, la velocidad del viento aumenta de acuerdo con la función v(t) = 20t + 5. Durante la segunda media hora de la salida de Andrew, el viento se mantiene estable a 15 mph. En otras palabras, la velocidad del viento viene dada por

Recordando que el bote de hielo de Andrew viaja al doble de la velocidad del viento, y suponiendo que se mueve en línea recta lejos de su punto de partida, ¿a qué distancia está Andrew de su punto de partida después de 1 hora?
Solución:
Para averiguar qué tan lejos viajó Andrew, necesitamos integrar su velocidad, que es el doble de la velocidad del viento. Entonces

Sustituyendo las expresiones que nos dieron v(t), obtenemos

Andrew está a 40 km de su punto de partida después de 1 hora. ♦
Ejercicio de control 5.4.3
Supongamos que, en lugar de permanecer constante durante la segunda media hora de la salida de Andrew, el viento comienza a amainar según la función \( v(t) = -10t + 15 \). En otras palabras, la velocidad del viento está dada por
\[ v(t) = \begin{cases} 20t + 5 & \text{para } 0 \leq t \leq \frac{1}{2} \\ -10t + 15 & \text{para } \frac{1}{2} \leq t \leq 1. \end{cases} \]Bajo estas condiciones, ¿a qué distancia de su punto de partida se encuentra Andrew después de 1 hora? ♦
Integrando funciones pares e impares
Vimos en el capítulo Funciones y sus Gráficas que una función par es una función en la que f (−x) = f (x) para todas las x en el dominio, es decir, la gráfica de la curva no cambia cuando x se reemplaza por −x. Las gráficas de funciones pares son simétricas sobre el eje y. Una función impar es aquella en la que f (−x) = – f (x) para todas las x en el dominio, y la gráfica de la función es simétrica con respecto al origen.
Las integrales de funciones pares, cuando los límites de integración son de −a a a, involucran dos áreas iguales, porque son simétricas alrededor del eje y. Las integrales de funciones impares, cuando los límites de integración son inversos aditivos [−a, a], se evalúan a cero porque las áreas por encima y por debajo del eje x son iguales.
REGLA 5.4_1: INTEGRALES DE FUNCIONES pares e impares
Para funciones pares continuas tales que \( f(-x) = f(x) \),
\[ \int_{-a}^{a} f(x) \, dx = 2 \int_{0}^{a} f(x) \, dx. \]Para funciones impares continuas tales que \( f(-x) = -f(x) \),
\[ \int_{-a}^{a} f(x) \, dx = 0. \]♦
EJEMPLO ILUSTRATIVO 5.4_6. Integrando una función par
Integrar la función par

y verifique que se mantenga la fórmula de integración para funciones pares.
Solución:
La simetría aparece en las gráficas de la figura 5.4_4. El gráfico (a) muestra la región debajo de la curva y arriba del eje x. Tenemos que acercarnos mucho a este gráfico para ver la región. El gráfico (b) muestra la región sobre la curva y debajo del eje x. El área con signo de esta región es negativa. Ambas vistas ilustran la simetría sobre el eje y de una función par. Tenemos

Para verificar la fórmula de integración para funciones pares, podemos calcular la integral de 0 a 2 y duplicarla, luego verificar para asegurarnos de obtener la misma respuesta.

Dado que 2⋅500/3 = 1000/3, hemos verificado la fórmula para funciones pares en este ejemplo particular.
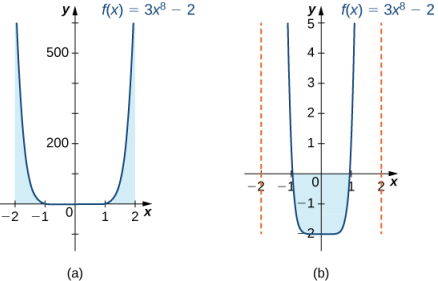
Figura 5.4_4 El gráfico (a) muestra el área positiva entre la curva y el eje x, mientras que el gráfico (b) muestra el área negativa entre la curva y el eje x. Ambas vistas muestran la simetría sobre el eje y. ♦
EJEMPLO ILUSTRATIVO 5.4_7. Integrando una función impar
Evalúe la integral definida de la función impar −5senx durante el intervalo [−π, π].
Solución:
El gráfico se muestra en la figura 5.4_5. Podemos ver la simetría sobre el origen por el área positiva sobre el eje x sobre [−π, 0], y el área negativa debajo del eje x sobre [0, π]. Tenemos
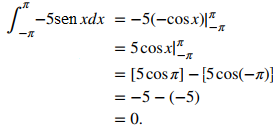

Figura 5.4_5 El gráfico muestra áreas entre una curva y el eje x para una función impar. ♦
Ejercicio de control 5.4.4
Integra la función \( \int_{-2}^{2} x^4 \, dx \). ♦
