| 9. Ecuaciones diferenciales | 9.6 Aplicaciones de ecuaciones lineales de segundo orden |
9.6.4 Movimiento bajo una fuerza central
Ahora estudiaremos el movimiento de un objeto que se mueve bajo la influencia de una fuerza central; es decir, una fuerza cuya magnitud en cualquier punto P que no sea el origen depende únicamente de la distancia de P al origen, y cuya dirección en P es paralela a la recta que conecta P y el origen, como se indica en la figura 9.6.4.1 para el caso donde la dirección de la fuerza en cada punto es hacia el origen. Las fuerzas gravitatorias son fuerzas centrales; por ejemplo, como se mencionó en la Sección 9.4.3, si asumimos que la Tierra es una esfera perfecta con densidad de masa constante, entonces la ley de gravitación de Newton afirma que la fuerza ejercida sobre un objeto por el campo gravitatorio de la Tierra es proporcional a la masa del objeto y inversamente proporcional al cuadrado de su distancia al centro de la Tierra, que tomamos como origen.
Figura 9.6.4.1
Si los vectores de posición inicial y velocidad de un objeto que se mueve bajo una fuerza central son paralelos, entonces el movimiento subsiguiente es a lo largo de la recta desde el origen hasta la posición inicial. Aquí supondremos que los vectores de posición inicial y velocidad no son paralelos; en este caso el movimiento subsiguiente está en el plano determinado por ellos. Por conveniencia, tomamos este como el plano xy. Consideraremos el problema de determinar la curva recorrida por el objeto. Llamamos a esta curva la órbita.
Podemos representar una fuerza central en términos de coordenadas polares
x = r cosθ, y = r senθ
como
F(r, θ) = f (r)(cos θ i + sen θ j).
Suponemos que f es continua para todo r > 0. La magnitud de F en (x, y) = (r cosθ, r senθ) es |f (r)|, por lo que depende solo de la distancia r desde el punto al origen la dirección de F es del punto al origen si f (r) < 0, o del origen al punto si f (r) > 0. Mostraremos que la órbita de un objeto con masa m moviéndose bajo esta fuerza está dada por
donde u es la solución de la ecuación diferencial
(y h es una constante definida a continuación.
La segunda ley de movimiento de Newton (F = ma) dice que las coordenadas polares r = r(t) y θ = θ(t) de la partícula satisfacen la ecuación diferencial vectorial
m(r cosθ i + r senθ j)′′ = f (r)(cosθ i + senθ j). (9.6.4.2)
Para tratar esta ecuación introducimos los vectores unitarios
e1 = cosθ i + senθ j y e2 = − senθ i + cosθ j.
Tenga en cuenta que e1 apunta en la dirección de aumento de r y e2 apunta en la dirección de aumento de θ (Figura 9.6.4.2); además,
(9.6.4.3)
y
e1 · e2 = cosθ(− senθ) + senθ cosθ = 0,
entonces e1 y e2 son perpendiculares. Recordando que la prima única (′) representa la diferenciación con respecto a t, vemos de (9.6.4.3) y la regla de la cadena que
e′1 = θ′e2 y e′2 = −θ′e1. (9.6.4.4)
Figura 9.6.4.2
Ahora podemos escribir (9.6.4.2) como
m(re1)′′ = f (r)e1. (9.6.4.5)
Pero
(re1)′ = r′e1 + re′1 = r′e1 + rθ′e2
(de (9.6.4.4)), y
Sustituyendo esto en (9.6.4.5) se obtiene
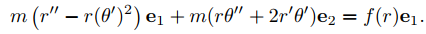
Al igualar los coeficientes de e1 y e2 en los dos lados de esta ecuación vemos que
mr′′ − r(θ′)2 = f (r) (9.6.4.6)
y
rθ′′ + 2r′θ′ = 0.
Multiplicando la última ecuación por r se obtiene
r2θ′′ + 2rr′θ′ = (r2θ′)′ = 0,
por lo que
r2θ′ = h, (9.6.4.7)
donde h es una constante que podemos escribir en términos de las condiciones iniciales como
h = r2(0)θ′(0).
Dado que los vectores de posición inicial y velocidad inicial son
r(0)e1(0) y r′(0)e1(0) + r(0)θ′(0)e2(0),
nuestra suposición de que estos dos vectores no son paralelos implica que θ′(0) ≠ 0, por lo que h ≠ 0.
Ahora sea u = 1/r. Entonces u2 = θ′/h (de (9.6.4.7)) y
lo que implica que
(9.6.4.8)
ya que
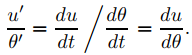
Derivando (9.6.4.8) con respecto a t se obtiene
lo que implica que
ya que θ′ = hu2.
Sustituyendo estas igualdades en (9.6.4.6) y recordando que r = 1/u se obtiene
y dividiendo por −mh2u2 se obtiene (9.6.4.1).
La ecuación (9.6.4.7) tiene la siguiente interpretación geométrica, que se conoce como Segunda Ley de Kepler.
Teorema 9.6.4.1
El vector de posición de un objeto que se mueve bajo una fuerza central barre áreas iguales en tiempos iguales; más precisamente, si θ(t1) ≤ θ(t2) entonces el área (con signo) del sector
(Figura 9.6.4.3) viene dada por
donde h = r2θ′, que hemos demostrado que es constante. ♦
Figura 9.6.4.3
Demostración:
Recuerde del cálculo que el área del sector sombreado en la figura 9.6.4.3 es
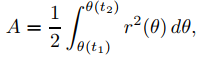
donde r = r(θ) es la representación polar de la órbita. Haciendo el cambio de variable θ = θ(t) se obtiene
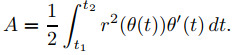(9.6.4.9)
Pero (9.6.4.7) y (9.6.4.9) implican que
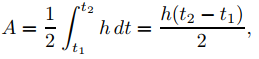
que completa la demostración. ♦
Movimiento bajo una fuerza de ley del cuadrado inverso
En el caso especial donde f (r) = −mk/r2 = −mku2, por lo que F puede interpretarse como una fuerza gravitacional, (9.6.4.1) se convierte en
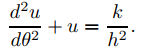(9.6.4.10)
La solución general de la ecuación complementaria.
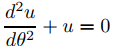
se puede escribir en forma de amplitud-fase como
u = Acos(θ − φ),
donde A ≥ 0 y φ es un ángulo de fase. Como up = k/h2 es una solución particular de (9.6.4.10), la solución general de (9.6.4.10) es
por lo tanto, la órbita está dada por
Lo que reescribimos como
(9.6.4.11)
donde
y e = Aρ.
Una curva que satisface (9.6.4.11) es una sección cónica con un foco en el origen (Ejercicio 1). La constante no negativa e es la excentricidad de la órbita, que es una elipse si e < 1 elipse (una circunferencia si e = 0), una parábola si e = 1 o una hipérbola si e > 1.
Figura 9.6.4.4
Si la órbita es una elipse, entonces los valores mínimo y máximo de r son
(la distancia del perihelio, alcanzada cuando θ = φ)
(la distancia del afelio, alcanzada cuando θ = φ + π).
La figura 9.6.4.4 muestra una órbita elíptica típica. El punto P de la órbita donde r = rmin es el perigeo y el punto A donde r = rmax es el apogeo.
Por ejemplo, la órbita de la Tierra alrededor del Sol es aproximadamente una elipse con e ≈ 0,017, rmin ≈ 91 × 106 millas y rmax ≈ 95 × 106 millas. El cometa Halley tiene una órbita aproximadamente elíptica muy alargada alrededor del sol, con e ≈ 0.967, rmin ≈ 55 × 106 millas y rmax ≈ 33 × 108 millas. Algunos cometas (del tipo no recurrente) tienen órbitas parabólicas o hiperbólicas.