El producto cruz

EL PRODUCTO CRUZ: Objetivos de aprendizaje

10.4.1 Calcule el producto cruza de dos vectores dados.
10.4.2 Usa determinantes para calcular un producto cruz.
10.4.3 Encuentre un vector ortogonal a dos vectores dados.
10.4.4 Determine áreas y volúmenes utilizando el producto cruz.
10.4.5 Calcule el torque dada la fuerza y el vector de posición.

Imagine a un mecánico girando una llave para apretar un perno. El mecánico aplica una fuerza al final de la llave. Esto crea rotación, o torque, que aprieta el perno. Podemos usar vectores para representar la fuerza aplicada por el mecánico y la distancia (radio) desde el perno hasta el final de la llave. Entonces, podemos representar el par mediante un vector orientado a lo largo del eje de rotación. Tenga en cuenta que el vector de torque es ortogonal tanto para el vector de fuerza como para el vector de radio.

En esta sección, desarrollamos una operación llamada producto cruz, que nos permite encontrar un vector ortogonal a dos vectores dados. Calcular el torque es una aplicación importante de los productos cruz, y examinamos el torque con más detalle después en la sección.

El producto cruz y sus propiedades

El producto punto es una multiplicación de dos vectores que da como resultado un escalar. En esta sección, presentamos un producto de dos vectores que genera un tercer vector ortogonal a los dos primeros. Considere cómo podríamos encontrar ese vector. Deje que u = ⟨u₁, u₂, u₃⟩ y v = ⟨v₁, v₂, v₃⟩ sean vectores distintos de cero. Queremos encontrar un vector w = ⟨w₁, w₂, w₃⟩ ortogonal a u y v, es decir, queremos encontrar w tal que u⋅w = 0 y v⋅w = 0. Por lo tanto, w₁, w₂ y w₃ deben satisfacer

u₁ w₁ + u₂ w₂ + u₃ w₃ = 0

v₁ w₁ + v₂ w₂ + v₃ w₃ = 0. 

Si multiplicamos la ecuación superior por v₃ y la ecuación inferior por u₃ y restamos, podemos eliminar la variable w₃, esto es

(u₁ v₃ − v₁ u₃) w₁ + (u₂ v₃ − v₂ u₃) w₂ = 0. 

Si seleccionamos

w₁ = u₂ v₃ − u₃ v₂

w₂ =− (u₁ v₃ − u₃ v₁), 

obtenemos un posible vector solución. Sustituir estos valores nuevamente en las ecuaciones originales da

w₃ = u₁ v₂ − u₂ v₁. 

Es decir, el vector

w = ⟨u₂ v₃ − u₃ v₂, − (u₁ v₃ − u₃ v₁), u₁ v₂ − u₂ v₁⟩ 

es ortogonal a u y v, lo que nos lleva a definir la siguiente operación, llamada producto cruz.

DEFINICIÓN. Producto cruz Sea u = ⟨u₁, u₂, u₃⟩ y v = ⟨v₁, v₂, v₃⟩. Entonces, el producto cruz u × v es el vector

Por la forma en que hemos desarrollado u × v, debe quedar claro que el producto cruz es ortogonal tanto para u como para v. Sin embargo, nunca está de más comprobarlo. Para mostrar que u × v es ortogonal a u, calculamos el producto escalar de u y u × v.

De manera similar, podemos mostrar que el producto cruza también es ortogonal a v.

EJEMPLO ILUSTRATIVO 10.4_1. Encontrar un producto cruz 

Sea p = ⟨−1, 2, 5⟩ y q = ⟨4, 0, −3⟩ (Figura 10.4_1). Encuentra p × q.

Figura 10.4_1 Encontrar el producto cruz para dos vectores dados.

Solución:

Sustituya los componentes de los vectores en la ecuación del producto cruz:

Aunque puede no ser obvio en la ecuación del producto cruz, la dirección de u × v viene dada por la regla de la derecha. Si levantamos la mano derecha con los dedos apuntando en la dirección de u, luego doblamos los dedos hacia el vector v, el pulgar apunta en la dirección del producto cruzo, como se muestra en la figura siguiente:

Observe lo que esto significa para la dirección de v × u. Si aplicamos la regla de la mano derecha a v × u, comenzamos con nuestros dedos apuntando en la dirección de v, luego doblamos nuestros dedos hacia el vector u. En este caso, el pulgar apunta en la dirección opuesta de u × v. (¡Intentalo!)

EJEMPLO ILUSTRATIVO 10.4_2. Anticonmutatividad del producto cruz

Sea u = ⟨0, 2, 1⟩ y v = ⟨3, −1, 0⟩. Calcule u × v y v × u y grafíquelos.

Solución:
Tenemos

Vemos que, en este caso, u × v = – (v × u) (Figura 10.4_4). Probamos esto en general más adelante en esta sección.

Los productos cruz de los vectores unitarios estándar i, j y k pueden ser útiles para simplificar algunos cálculos, así que consideremos estos productos cruz. Una aplicación directa de la definición muestra que

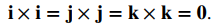
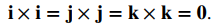
Además, debido a que el producto cruz de dos vectores es ortogonal a cada uno de estos vectores, sabemos que el producto cruz de i y j es paralelo a k. Del mismo modo, el producto vectorial de i y k es paralelo a j, y el producto vectorial de j y k es paralelo a i. Podemos usar la regla de la mano derecha para determinar la dirección de cada producto. Entonces tenemos

Estas fórmulas son útiles más tarde.

EJEMPLO ILUSTRATIVO 10.4_3. Producto cruz de vectores de unidad estándar

Encuentre i × (j × k).

Solución:

Sabemos que j × k = i. Por lo tanto, i × (j × k) = i × i = 0.

Como hemos visto, el producto punto a menudo se llama producto escalar porque da como resultado un escalar. El producto cruz da como resultado un vector, por lo que a veces se denomina producto vectorial. Estas operaciones son versiones de multiplicación de vectores, pero tienen propiedades y aplicaciones muy diferentes. Exploremos algunas propiedades del producto cruz. Probamos solo algunas de ellas. Las pruebas de las otras propiedades se dejan como ejercicios.

TEOREMA 10.4_1. Propiedades del producto cruz Supongamos que u, v y w son vectores en el espacio, y que c sea un escalar. i. u × v = -(v × u) Propiedad anticonmutativa ii. u × (v + w) = u × v + u × w Propiedad distributiva iii. c(u × v) = (cu) × v = u × (cv) Multiplicación por una constante iv. u × 0 = 0 × u = 0 Producto cruza del vector cero v. v × v = 0 Producto cruz de un vector consigo mismo vi. u · (v × w) = (u × v) · w Producto escalar triple

Prueba

Para la propiedad i., Queremos mostrar u × v = – (v × u). Tenemos

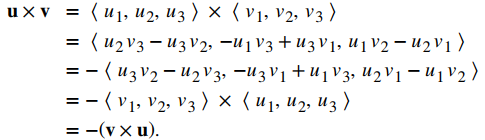
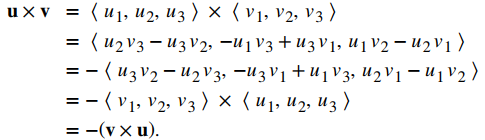
A diferencia de la mayoría de las operaciones que hemos visto, el producto cruz no es conmutativo. Esto tiene sentido si pensamos en la regla de la mano derecha.

Para la propiedad iv., Esto se deduce directamente de la definición del producto cruz. Tenemos

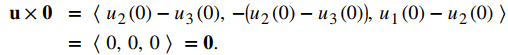
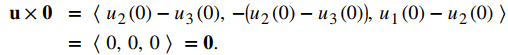
Entonces, por propiedad i., 0 × u = 0 también. Recuerde que el producto escalar de un vector y el vector cero es el escalar 0, mientras que el producto cruz de un vector con el vector cero es el vector 0.
Propiedad vi. se parece a la propiedad asociativa, pero tenga en cuenta el cambio en las operaciones:

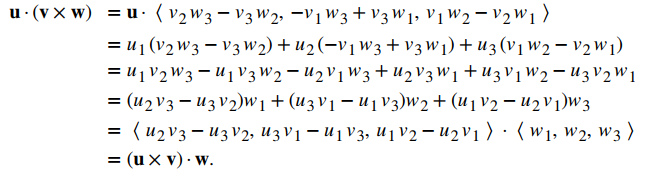
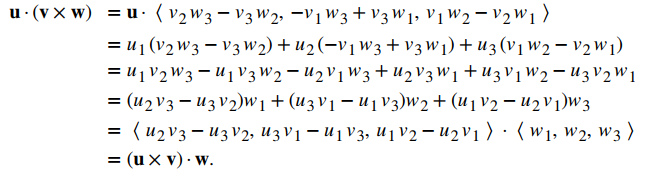
EJEMPLO ILUSTRATIVO 10.4_4. Uso de las propiedades del producto cruz

Use las propiedades del producto cruzado para calcular (2i × 3j) × j.

Solución: