COORDENADAS CILÍNDRICAS Y ESFÉRICAS: Objetivos de aprendizaje
10.7.1. Convierte de coordenadas cilíndricas a rectangulares.
10.7.2. Convierte de coordenadas rectangulares a cilíndricas.
10.7.3. Convierte de coordenadas esféricas a rectangulares.
10.7.4. Convierte de coordenadas rectangulares a esféricas.
El sistema de coordenadas cartesianas proporciona una forma sencilla de describir la ubicación de los puntos en el espacio. Sin embargo, algunas superficies pueden ser difíciles de modelar con ecuaciones basadas en el sistema cartesiano. Este es un problema familiar; recuerde que en dos dimensiones, las coordenadas polares a menudo proporcionan un sistema alternativo útil para describir la ubicación de un punto en el plano, particularmente en casos que involucran círculos. En esta sección, veremos dos formas diferentes de describir la ubicación de los puntos en el espacio, ambas basadas en extensiones de coordenadas polares. Como su nombre lo indica, las coordenadas cilíndricas son útiles para tratar problemas que involucran cilindros, como calcular el volumen de un tanque de agua redondo o la cantidad de aceite que fluye a través de una tubería. Del mismo modo, las coordenadas esféricas son útiles para tratar problemas relacionados con esferas, como encontrar el volumen de estructuras abovedadas.
Coordenadas Cilíndricas
Cuando expandimos el sistema tradicional de coordenadas cartesianas de dos dimensiones a tres, simplemente agregamos un nuevo eje para modelar la tercera dimensión. Comenzando con coordenadas polares, podemos seguir este mismo proceso para crear un nuevo sistema de coordenadas tridimensional, llamado sistema de coordenadas cilíndricas. De esta manera, las coordenadas cilíndricas proporcionan una extensión natural de las coordenadas polares a tres dimensiones.
DEFINICIÓN. Sistema de coordenadas cilíndricasEn el sistema de coordenadas cilíndricas, un punto en el espacio (Figura 10.7_1) está representado por el triple ordenado (r, θ, z), donde ♦ (r, θ) son las coordenadas polares de la proyección del punto en el plano xy |

En el plano xy, el triángulo rectángulo que se muestra en la figura 10.7_1 proporciona la clave para la transformación entre coordenadas cilíndricas y cartesianas, o rectangulares.
TEOREMA 140.7.1. Conversión entre coordenadas cilíndricas y cartesianasLas coordenadas rectangulares (x, y, z) y las coordenadas cilíndricas (r, θ, z) de un punto están relacionadas de la siguiente manera:
|
||||||
Como cuando discutimos la conversión de coordenadas rectangulares a coordenadas polares en dos dimensiones, debe notarse que la ecuación tanθ = y/x tiene un número infinito de soluciones. Sin embargo, si restringimos θ a valores entre 0 y 2π, entonces podemos encontrar una solución única basada en el cuadrante del plano xy en el que se encuentra el punto original (x, y, z). Tenga en cuenta que si x = 0, entonces el valor de θ es π/2,3π/2 o 0, dependiendo del valor de y.
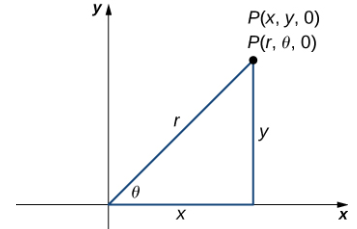
Observe que estas ecuaciones se derivan de las propiedades de los triángulos rectángulos. Para que sea fácil de ver, considere el punto P en el plano xy con coordenadas rectangulares (x, y, 0) y con coordenadas cilíndricas (r, θ, 0), como se muestra en la siguiente figura.
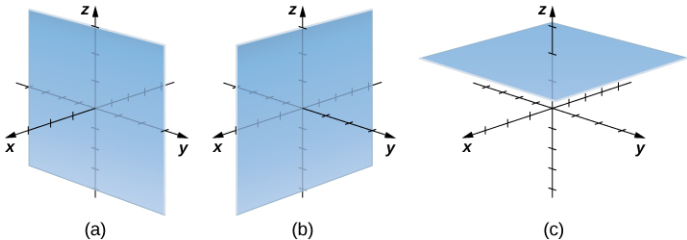
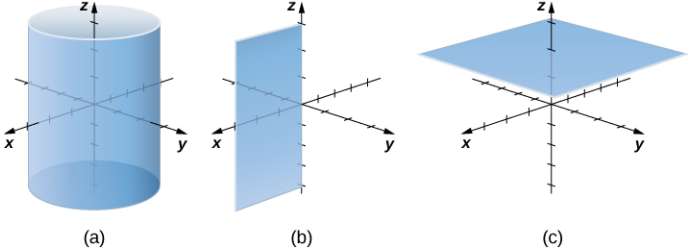
Consideremos las diferencias entre las coordenadas rectangulares y cilíndricas al observar las superficies generadas cuando cada una de las coordenadas se mantiene constante. Si c es una constante, entonces en coordenadas rectangulares, las superficies de la forma x = c, y = c, o z = c son todos planos. Los planos de estas formas son paralelos al plano yz, al plano xz y al plano xy, respectivamente. Cuando convertimos a coordenadas cilíndricas, la coordenada z no cambia. Por lo tanto, en coordenadas cilíndricas, las superficies de la forma z = c son planos paralelos al plano xy. Ahora, pensemos en las superficies de la forma r = c. Los puntos en estas superficies están a una distancia fija del eje z. En otras palabras, estas superficies son cilindros circulares verticales. Por último, ¿qué pasa con θ = c? Los puntos en una superficie de la forma θ = c están en un ángulo fijo desde el eje x, lo que nos da un semiplano que comienza en el eje z (Figura 10.7_3 y Figura 10.7_4).
EJEMPLO ILUSTRATIVO 10.7_1. Conversión de coordenadas cilíndricas a rectangulares
Trace el punto con coordenadas cilíndricas (4, 2π/3, −2) y exprese su ubicación en coordenadas rectangulares.
Solución:
La conversión de coordenadas cilíndricas a rectangulares requiere una aplicación simple de las ecuaciones numeradas en “Conversión entre coordenadas cilíndricas y cartesianas”:

El punto con coordenadas cilíndricas (4, 2π/3, −2) tiene coordenadas rectangulares (−2, 2√3, −2) (ver la siguiente figura).
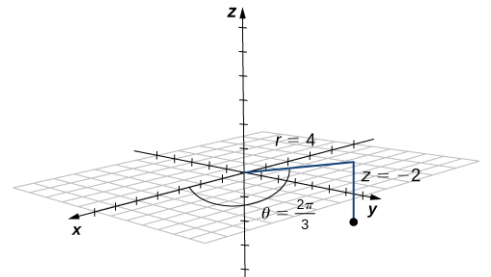
Figura 10.7_5 La proyección del punto en el plano xy es de 4 unidades desde el origen. La línea desde el origen hasta la proyección del punto forma un ángulo de 2π/3 con el eje x positivo. El punto se encuentra 2 unidades debajo del plano xy.
Si este proceso parece familiar, es con buena razón. Este es exactamente el mismo proceso que seguimos en “Introducción a las ecuaciones paramétricas y las coordenadas polares” para convertir de coordenadas polares a coordenadas rectangulares bidimensionales.
EJEMPLO ILUSTRATIVO 10.7_2 Conversión de coordenadas rectangulares a cilíndricas
Convierta las coordenadas rectangulares (1, −3, 5) en coordenadas cilíndricas.
Solución:
Use el segundo conjunto de ecuaciones de Conversión entre coordenadas cilíndricas y cartesianas para traducir de coordenadas rectangulares a coordenadas cilíndricas:
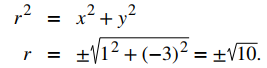
Elegimos la raíz cuadrada positiva, entonces r = √10. Ahora, aplicamos la fórmula para encontrar θ. En este caso, y es negativo y x es positivo, lo que significa que debemos seleccionar el valor de θ entre 3π/2 y 2π:

En este caso, las coordenadas z son las mismas en coordenadas rectangulares y cilíndricas:
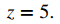
El punto con coordenadas rectangulares (1, −3, 5) tiene coordenadas cilíndricas aproximadamente iguales a (√10, 5.03, 5).
El uso de coordenadas cilíndricas es común en campos como la física. Los físicos que estudian las cargas eléctricas y los condensadores utilizados para almacenar estas cargas han descubierto que estos sistemas a veces tienen una simetría cilíndrica. Estos sistemas tienen ecuaciones de modelado complicadas en el sistema de coordenadas cartesianas, lo que dificulta su descripción y análisis. Las ecuaciones a menudo se pueden expresar en términos más simples usando coordenadas cilíndricas. Por ejemplo, el cilindro descrito por la ecuación x^2 + y^2 = 25 en el sistema cartesiano puede representarse mediante la ecuación cilíndrica r = 5.
EJEMPLO ILUSTRATIVO 10.7_3 Identificación de superficies en el sistema de coordenadas cilíndricas
Describa las superficies con las ecuaciones cilíndricas dadas.

Solución:
a. Cuando el ángulo θ se mantiene constante mientras r y z pueden variar, el resultado es un semiplano (ver la siguiente figura).
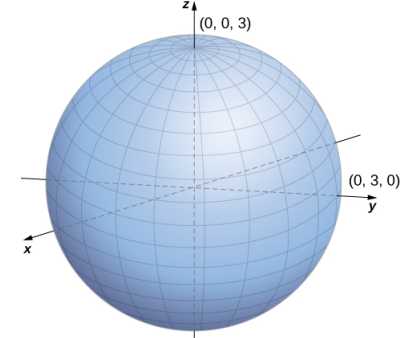
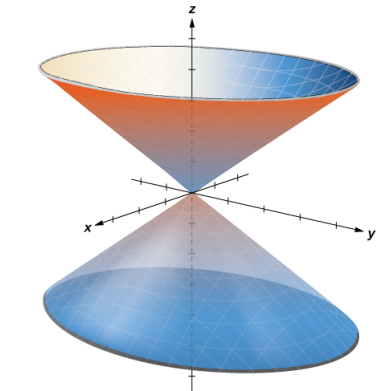
b. Sustituya r^2 = x^2 + y^2 en la ecuación r^2 + z^2 = 9 para expresar la forma rectangular de la ecuación: x^2 + y^2 + z^2 = 9. Esta ecuación describe una esfera centrada en el origen con radio 3 (ver la siguiente figura).
c. Para describir la superficie definida por la ecuación z = r, ¿es útil examinar trazas paralelas al plano xy? Por ejemplo, la traza en el plano z = 1 es la circunferencia r = 1, la traza en el plano z = 3 es la circunferencia r = 3, y así sucesivamente. Cada rastro es una circunferencia. A medida que aumenta el valor de z, el radio de la circunferencia también aumenta. La superficie resultante es un cono (ver la siguiente figura).

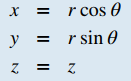
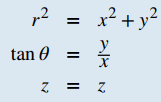
una ayuda por favor : ojo B =11
Se A un punto en el espacio que en coordenadas cartesianas está dado por la posición Bi + (B+3)j + 4k,
sobre esta posición se construye el vector C = 2i + 4j – 5k.
a) Muestre el vector C en coordenadas cilíndricas.
b) Muestre el vector C en coordenadas esféricas.
What’s up colleagues, how is everything, and
what you would like to say on the topic of this
piece of writing, in my view its truly awesome in support of me.
Great content! Super high-quality! Keep it up! 🙂