| 4. Aplicaciones de la derivada | Ejercicios propuestos para el Capítulo 4.5 |

4.5 DERIVADAS Y LA FORMA DE UNA GRÁFICA

Objetivos de aprendizaje:

4.5.1 Explicar cómo el signo de la primera derivada afecta la forma de la gráfica de una función.
4.5.2. Mostrar la primera prueba de la derivada para puntos críticos.
4.5.3. Utilizar los puntos de concavidad e inflexión para explicar cómo el signo de la segunda derivada afecta la forma de la gráfica de una función.
4.5.4. Explicar la prueba de concavidad para una función durante un intervalo abierto.
4.5.5. Explicar la relación entre una función y su primera y segunda derivada.
4.5.6. Mostrar la prueba de la segunda derivada para extremos locales.

Anteriormente en este capítulo declaramos que si una función f tiene un extremo local en un punto c, entonces c debe ser un punto crítico de f. Sin embargo, no se garantiza que una función tenga un extremo local en un punto crítico. Por ejemplo, f (x) = x³ tiene un punto crítico en x = 0 ya que f ′(x) = 3x² es cero en x = 0, pero f no tiene un extremo local en x = 0. Usando los resultados de la sección anterior, ahora podemos determinar si un punto crítico de una función realmente corresponde a un valor extremo local. En esta sección, también vemos cómo la segunda derivada proporciona información sobre la forma de una gráfica al describir si la gráfica de una función se curva hacia arriba o hacia abajo.

Prueba de la primera derivada

El corolario 3 del teorema del valor medio mostró que si la derivada de una función es positiva durante un intervalo I, entonces la función aumentará sobre I. Por otro lado, si la derivada de la función es negativa durante un intervalo I, entonces la función está disminuyendo sobre I como se muestra en la siguiente figura.

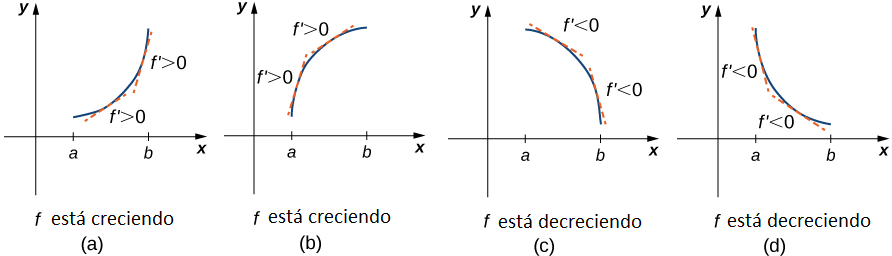
      Una función continua f tiene un máximo local en el punto c si y solo si f cambia de creciente a de creciente en el punto c. De manera similar, f tiene un mínimo local en c si y solo si f cambia de decreciente a creciente en c. Si f es una función continua en un intervalo I que contiene c y diferenciable sobre I, excepto posiblemente en c, la única forma en que f puede cambiar de creciente a decreciente (o viceversa) en el punto c es si f ′ cambia de signo a medida que x aumenta a través de c. Si f es diferenciable en c, la única forma en que f ′ puede cambiar de signo a medida que x aumenta a través de c es si f ′(c) = 0. Por lo tanto, para una función f que es continua durante un intervalo I que contiene c y diferenciable sobre I, excepto posiblemente en c, la única forma en que f puede cambiar de creciente a decreciente (o viceversa) es si f ′(c) = 0 o f ′(c) no está definido. En consecuencia, para localizar extremos locales para una función f, buscamos puntos c en el dominio de f de modo que f ′(c) = 0 o f ′(c) no esté definida. Recuerde que tales puntos se llaman puntos críticos de f.

Tenga en cuenta que f no necesita tener un extremo local en un punto crítico. Los puntos críticos son candidatos para extremos locales solamente. En la figura 4.5.2, mostramos que si una función continua f tiene un extremo local, debe ocurrir en un punto crítico, pero una función puede no tener un extremo local en un punto crítico. Mostramos que si f tiene un extremo local en un punto crítico, entonces el signo de f ′ cambia a medida que x aumenta a través de ese punto.

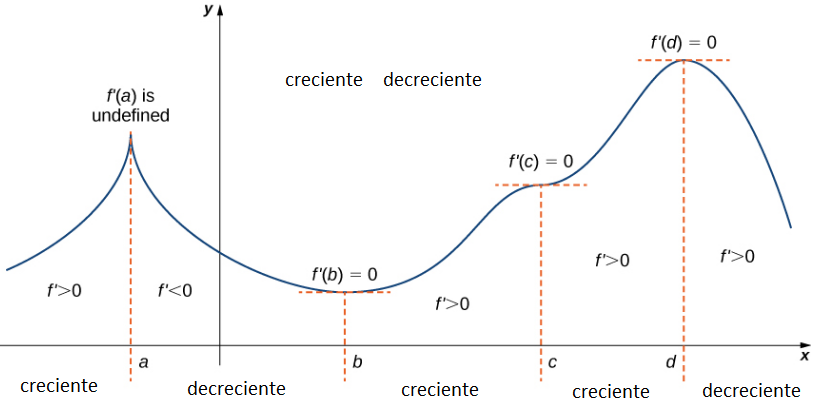
Usando la figura 4.5.2, resumimos los principales resultados con respecto a los extremos locales.

• Si una función continua \(f\) tiene un extremo local, debe ocurrir en un punto crítico \(c\).
• La función tiene un extremo local en el punto crítico \(c\) si y solo si la derivada \(f’\) cambia de signo cuando \(x\) aumenta a través de \(c\).
• Por lo tanto, para probar si una función tiene un extremo local en un punto crítico \(c\), debemos determinar el signo de \(f'(x)\) a la izquierda y a la derecha de \(c\).

Teorema 4.5.1.  Prueba de la primera derivada

Suponga que \(f\) es una función continua sobre un intervalo \(I\) que contiene un punto crítico \(c\). Si \(f\) es diferenciable sobre \(I\), excepto posiblemente en el punto \(c\), entonces \(f(c)\) satisface una de las siguientes descripciones:

1. Si \(f’\) cambia de signo de positivo cuando \(x < c\) a negativo cuando \(x > c\), entonces \(f(c)\) es un máximo local de \(f\).
2. Si \(f’\) cambia de signo de negativo cuando \(x < c\) a positivo cuando \(x > c\), entonces \(f(c)\) es un mínimo local de \(f\).
3. Si \(f’\) tiene el mismo signo para \(x < c\) y \(x > c\), entonces \(f(c)\) no es ni un máximo local ni un mínimo local de \(f\). ♦

Estrategia para resolver problemas: Utilizar la prueba de la primera derivada

Considere una función \(f\) que es continua sobre un intervalo \(I\).

1. Encuentra todos los puntos críticos de \(f\) y divide el intervalo \(I\) en intervalos más pequeños usando los puntos críticos como puntos extremos.
2. Analiza el signo de \(f’\) en cada uno de los subintervalos. Si \(f’\) es continua sobre un subintervalo dado (lo cual es típicamente el caso), entonces el signo de \(f’\) en ese subintervalo no cambia y, por lo tanto, puede ser determinado eligiendo un punto de prueba arbitrario \(x\) en ese subintervalo y evaluando el signo de \(f’\) en ese punto de prueba. Usa el análisis de signo para determinar si \(f\) es creciente o decreciente sobre ese intervalo.

   Nota: Si \(f’\) no es continua a lo largo de \(I\), entonces incluye los puntos de discontinuidad junto con los puntos críticos como puntos extremos al dividir \(I\) en subintervalos.

3. Usa la Prueba de la Primera Derivada y los resultados del paso 2 para determinar si \(f\) tiene un máximo local, un mínimo local o ninguno en cada uno de los puntos críticos. ♦

Ejemplo ilustrativo 4.5.1: Usando la Prueba de la Primera Derivada para Encontrar Extremos Locales

Usa la prueba de la primera derivada para encontrar la ubicación de todos los extremos locales para

\[f(x) = x^3 – 3x^2 – 9x – 1.\]

Usa una herramienta de graficación para confirmar tus resultados.

Solución:

Paso 1. La derivada es \(f'(x) = 3x^2 – 6x – 9\). Para encontrar los puntos críticos, necesitamos encontrar dónde \(f'(x) = 0\). Factorizando el polinomio, concluimos que los puntos críticos deben satisfacer

\[3(x^2 – 2x – 3) = 3(x – 3)(x + 1) = 0.\]

Por lo tanto, los puntos críticos son \(x = 3, -1\). Ahora dividimos el intervalo \((-\infty, \infty)\) en los intervalos más pequeños \((-\infty, -1)\), \((-1, 3)\) y \((3, \infty)\).

Paso 2. Dado que \(f’\) es una función continua, para determinar el signo de \(f'(x)\) sobre cada subintervalo, es suficiente elegir un punto sobre cada uno de los intervalos \((-\infty, -1)\), \((-1, 3)\) y \((3, \infty)\) y determinar el signo de \(f’\) en cada uno de estos puntos. Por ejemplo, elijamos \(x = -2\), \(x = 0\) y \(x = 4\) como puntos de prueba.

Intervalo	Punto de Prueba	Signo de \(f'(x) = 3(x – 3)(x + 1)\) en el Punto de Prueba	Conclusión
\((-\infty, -1)\)	\(x = -2\)	\( (+)(-) (-) = + \)	\(f\) es creciente.
\((-1, 3)\)	\(x = 0\)	\( (+) (-) (+) = – \)	\(f\) es decreciente.
\((3, \infty)\)	\(x = 4\)	\( (+) (+) (+) = + \)	\(f\) es creciente.

Paso 3. Dado que \(f’\) cambia de signo de positivo a negativo cuando \(x\) aumenta a través de \(-1\), \(f\) tiene un máximo local en \(x = -1\). Dado que \(f’\) cambia de signo de negativo a positivo cuando \(x\) aumenta a través de \(3\), \(f\) tiene un mínimo local en \(x = 3\). Estos resultados analíticos concuerdan con la siguiente gráfica.

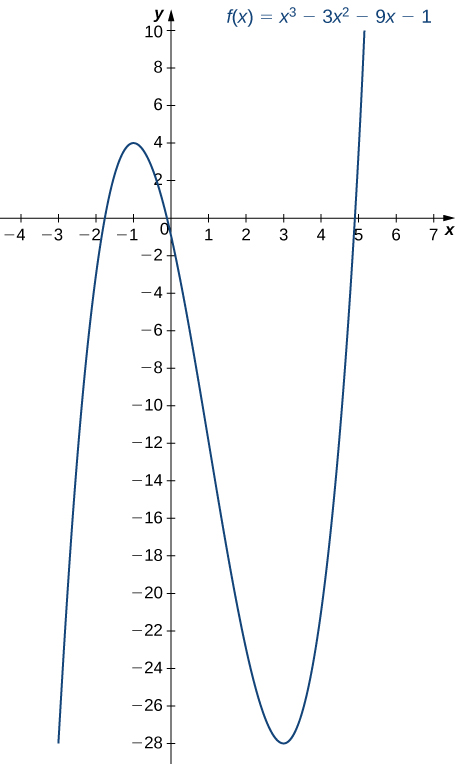
Figura 4.5.3 La función f tiene un máximo en x = −1 y un mínimo en x = 3. ♦

Ejercicio de control 4.5.1

Usa la prueba de la primera derivada para localizar todos los extremos locales para \[f(x) = -x^3 + \frac{3}{2}x^2 + 18x.\] ♦

Ejemplo ilustrativo 4.5.2: Usando la Prueba de la Primera Derivada

Usa la prueba de la primera derivada para localizar todos los extremos locales para \[f(x) = 5x^{1/3} – x^{5/3}.\] Usa una herramienta de graficación para confirmar tus resultados.

Solución:

Paso 1. La derivada es

\[f'(x) = \frac{5}{3}x^{-2/3} – \frac{5}{3}x^{2/3} = \frac{5 – 5x^{4/3}}{3x^{2/3}} = \frac{5(1 – x^{4/3})}{3x^{2/3}}.\]

La derivada \(f'(x) = 0\) cuando \(1 – x^{4/3} = 0\). Por lo tanto, \(f'(x) = 0\) en \(x = \pm 1\). La derivada \(f'(x)\) es indefinida en \(x = 0\). Por lo tanto, tenemos tres puntos críticos: \(x = 0\), \(x = 1\) y \(x = -1\). Consecuentemente, dividimos el intervalo \((-\infty, \infty)\) en los intervalos más pequeños \((-\infty, -1)\), \((-1, 0)\), \((0, 1)\) y \((1, \infty)\).

Paso 2. Dado que \(f’\) es continua sobre cada subintervalo, es suficiente elegir un punto de prueba \(x\) en cada uno de los intervalos del paso 1 y determinar el signo de \(f’\) en cada uno de estos puntos. Los puntos \(x = -2\), \(x = -\frac{1}{2}\), \(x = \frac{1}{2}\) y \(x = 2\) son puntos de prueba para estos intervalos.

Intervalo	Punto de Prueba	Signo de \(f'(x) = \frac{5(1 – x^{4/3})}{3x^{2/3}}\) en el Punto de Prueba	Conclusión
\((-\infty, -1)\)	\(x = -2\)	\(\frac{(+)(-)}{+} = -\)	\(f\) es decreciente.
\((-1, 0)\)	\(x = -\frac{1}{2}\)	\(\frac{(+)(+)}{+} = +\)	\(f\) es creciente.
\((0, 1)\)	\(x = \frac{1}{2}\)	\(\frac{(+)(+)}{+} = +\)	\(f\) es creciente.
\((1, \infty)\)	\(x = 2\)	\(\frac{(+)(-)}{+} = -\)	\(f\) es decreciente.

Paso 3. Dado que \(f\) es decreciente en el intervalo \((-\infty, -1)\) y creciente en el intervalo \((-1, 0)\), \(f\) tiene un mínimo local en \(x = -1\). Dado que \(f\) es creciente en el intervalo \((-1, 0)\) y en el intervalo \((0, 1)\), \(f\) no tiene un extremo local en \(x = 0\). Dado que \(f\) es creciente en el intervalo \((0, 1)\) y decreciente en el intervalo \((1, \infty)\), \(f\) tiene un máximo local en \(x = 1\). Los resultados analíticos concuerdan con la siguiente gráfica.

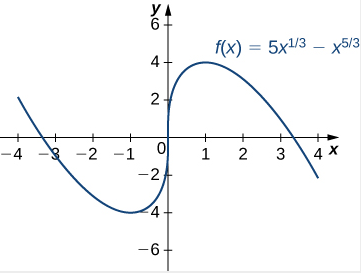
Figura 4.5.4 La función f tiene un mínimo local en x = −1 y un máximo local en x = 1. ♦

Ejercicio de control 4.5.2

Usa la prueba de la primera derivada para localizar todos los extremos locales para \[f(x) = \sqrt[3]{x – 1}.\] ♦

Concavidad y puntos de inflexión

Ahora sabemos cómo determinar dónde una función está creciendo o decreciendo. Sin embargo, hay otro tema a considerar con respecto a la forma del gráfico de una función. Si el gráfico se curva, ¿se curva hacia arriba o hacia abajo? Esta noción se llama concavidad de la función.

La figura 4.5.2 (a) muestra una función f con una gráfica que se curva hacia arriba. A medida que x aumenta, la pendiente de la recta tangente aumenta. Por lo tanto, dado que la derivada aumenta a medida que x aumenta, f ‘ es una función creciente. Decimos que esta función f es cóncava hacia arriba. La figura 4.5.2 (b) muestra una función f que se curva hacia abajo. A medida que x aumenta, la pendiente de la recta tangente disminuye. Como la derivada disminuye a medida que aumenta x, f ‘ es una función decreciente. Decimos que esta función f es cóncava hacia abajo.

Definición 4.5.1.  Concavidad

Sea f una función que se puede diferenciar en un intervalo abierto I. Si f ′ aumenta sobre I, decimos que f es cóncavo hacia arriba sobre I. Si f ′ disminuye sobre I, decimos que f es cóncavo hacia abajo sobre I. ♦

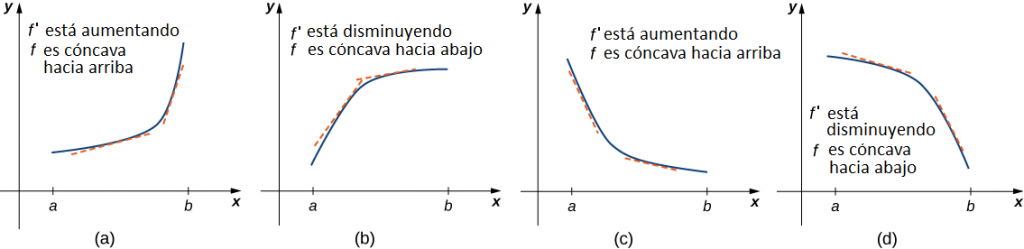
       En general, sin tener la gráfica de una función f, ¿cómo podemos determinar su concavidad? Por definición, una función f es cóncava hacia arriba si f ′ está aumentando. Por el Corolario 3, sabemos que si f ′ es una función diferenciable, entonces f ′ aumenta si su segunda derivada f ′′ (x) > 0. Por lo tanto, una función f que es dos veces diferenciable es cóncava hacia arriba cuando f ′′ (x) > 0. Del mismo modo, una función f es cóncava hacia abajo si f ′ está disminuyendo. Sabemos que una función diferenciable f ′ está disminuyendo si su segunda derivada f ′′ (x) < 0. Por lo tanto, una función dos veces diferenciable f es cóncava hacia abajo cuando f ′′ (x) < 0. La aplicación de esta lógica se conoce como prueba de concavidad.

Teorema 4.5.2.  Prueba de concavidad

Sea \(f\) una función que es dos veces diferenciable sobre un intervalo \(I\).

1. Si \(f′′(x) > 0\) para toda \(x \in I\), entonces \(f\) es cóncava hacia arriba sobre \(I\).
2. Si \(f′′(x) < 0\) para toda \(x \in I\), entonces \(f\) es cóncava hacia abajo sobre \(I\). ♦

      Concluimos que podemos determinar la concavidad de una función f observando la segunda derivada de f. Además, observamos que una función f puede cambiar la concavidad (Figura 4.5.6). Sin embargo, una función continua puede cambiar la concavidad solo en un punto x si f ″ (x) = 0 o f ″ (x) no está definido. En consecuencia, para determinar los intervalos donde una función f es cóncava hacia arriba y hacia abajo, buscamos aquellos valores de x donde f ″ (x) = 0 o f ″ (x) no está definida. Cuando hemos determinado estos puntos, dividimos el dominio de f en intervalos más pequeños y determinamos el signo de f ″ sobre cada uno de estos intervalos más pequeños. Si f ″ cambia de signo cuando pasamos por un punto x, entonces f cambia la concavidad. Es importante recordar que una función f puede no cambiar la concavidad en un punto x incluso si f ″(x) = 0 o f ″(x) no está definida. Sin embargo, si f cambia la concavidad en un punto a y f es continuo en a, decimos que el punto (a, f(a)) es un punto de inflexión de f.

Definición 4.5.2. Punto de inflexión

Si  f es continua en a y f cambia la concavidad en a, el punto (a, f (a)) es un punto de inflexión de f. ♦

Ejemplo ilustrativo 4.5.3: Prueba de Concavidad

Para la función \[f(x) = x^3 – 6x^2 + 9x + 30,\] determina todos los intervalos donde \(f\) es cóncava hacia arriba y todos los intervalos donde \(f\) es cóncava hacia abajo. Enumera todos los puntos de inflexión para \(f\). Usa una herramienta de graficación para confirmar tus resultados.

Solución:

Para determinar la concavidad, necesitamos encontrar la segunda derivada \(f′′(x)\). La primera derivada es

\[f′(x) = 3x^2 – 12x + 9,\]

así que la segunda derivada es

\[f′′(x) = 6x – 12.\]

Si la función cambia de concavidad, ocurre cuando \(f′′(x) = 0\) o cuando \(f′′(x)\) es indefinida. Dado que \(f′′\) está definida para todos los números reales \(x\), solo necesitamos encontrar dónde \(f′′(x) = 0\). Resolviendo la ecuación \(6x – 12 = 0\), vemos que \(x = 2\) es el único lugar donde \(f\) podría cambiar de concavidad. Ahora probamos puntos sobre los intervalos \((-\infty, 2)\) y \((2, \infty)\) para determinar la concavidad de \(f\). Los puntos \(x = 0\) y \(x = 3\) son puntos de prueba para estos intervalos.

Intervalo	Punto de Prueba	Signo de \(f′′(x) = 6x – 12\) en el Punto de Prueba	Conclusión
\((-\infty, 2)\)	\(x = 0\)	\(-\)	\(f\) es cóncava hacia abajo
\((2, \infty)\)	\(x = 3\)	\(+\)	\(f\) es cóncava hacia arriba.

Concluimos que \(f\) es cóncava hacia abajo en el intervalo \((-\infty, 2)\) y cóncava hacia arriba en el intervalo \((2, \infty)\). Dado que \(f\) cambia de concavidad en \(x = 2\), el punto \((2, f(2)) = (2, 32)\) es un punto de inflexión.

La Figura 4.5.7 confirma los resultados analíticos.

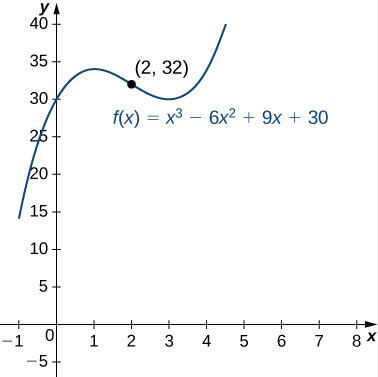
Figura 4.5.7 La función dada tiene un punto de inflexión en (2,32) donde la gráfica cambia de concavidad. ♦

Ejercicio de control 4.5.3

Para \(f(x) = -x^3 + \frac{3}{2}x^2 + 18x,\) encuentra todos los intervalos donde \(f\) es cóncava hacia arriba y todos los intervalos donde \(f\) es cóncava hacia abajo. ♦

Ahora resumimos, en la Tabla 4.5.1, la información que las derivadas primera y segunda de una función f proporcionan sobre la gráfica de f, e ilustramos esta información en la Figura 4.5.4.

Signo de  f ′	‘Signo de f ′′	¿f aumenta o disminuye?	Concavidad
Positivo	Positivo	Aumenta	Cóncava hacia arriba
Positivo	Negativo	Aumenta	Cóncava hacia abajo
Negativo	Positivo	Disminuye	Cóncava hacia arriba
Negativo	Negativo	Disminuye	Cóncava hacia abajo

Tabla 4.5.1  Lo que nos dicen las derivadas sobre las gráficas

Prueba de la segunda derivada

La prueba de la primera derivada proporciona una herramienta analítica para encontrar extremos locales, pero la segunda derivada también se puede usar para localizar valores extremos. Usar la segunda derivada a veces puede ser un método más simple que usar la primera derivada.

Sabemos que si una función continua tiene extremos locales, debe ocurrir en un punto crítico. Sin embargo, una función no necesita tener extremos locales en un punto crítico. Aquí examinamos cómo se puede usar la prueba de la segunda derivada para determinar si una función tiene un extremo local en un punto crítico. Sea f una función dos veces diferenciable de tal manera que f ′(a) = 0 y f ′′ es continua durante un intervalo abierto I que contiene a a. Supongamos que f ′′(a) < 0. Como f ′′ es continua sobre I, f ′′(x) < 0 para todo x ∈ I (Figura 4.5.7). Luego, según el Corolario 3, f ′ es una función decreciente sobre I. Como f ′ (a) = 0, concluimos que para todos x ∈ I, f ′ (x) > 0 si x < a y f ′ (x) < 0 si x > a. Por lo tanto, mediante la prueba de la primera derivada, f tiene un máximo local en x = a. Por otro lado, supongamos que existe un punto b tal que f ′(b) = 0 pero f ′′(b) > 0. Como f ” es continuo en un intervalo abierto I que contiene a b, entonces f ” (x) > 0 para todo x ∈ I (Figura 4.5.6). Luego, según el Corolario 3, f ′ es una función creciente sobre I. Como f ′(b) = 0, concluimos que para todos x ∈ I, f ′(x) < 0 si x < b y f ′ (x) > 0 si x > b. Por lo tanto, mediante la prueba  de la primera prueba derivada, f tiene un mínimo local en x = b.

Figura 4.5.7  Considere una función dos veces diferenciable f tal que f ″ sea continua. Como f ‘(a) = 0 y f ″(a) < 0, hay un intervalo I que contiene a a tal que para todo x en I, f aumenta si x < a y f disminuye si x > a. Como resultado, f tiene un máximo local en x = a. Dado que f ‘(b) = 0 y f ″(b) > 0, hay un intervalo I que contiene a b tal que para todas las x en I, f disminuye si x < b y f aumenta si x > b. Como resultado, f tiene un mínimo local en x = b.

Teorema 4.5.3.  Prueba de la segunda derivada

Suponga que \(f′(c) = 0\), \(f′′\) es continua sobre un intervalo que contiene a \(c\).

1. Si \(f′′(c) > 0\), entonces \(f\) tiene un mínimo local en \(c\).
2. Si \(f′′(c) < 0\), entonces \(f\) tiene un máximo local en \(c\).
3. Si \(f′′(c) = 0\), entonces la prueba no es concluyente. ♦

Ejemplo ilustrativo 4.5.4: Usando la Prueba de la Segunda Derivada

Usa la segunda derivada para encontrar la ubicación de todos los extremos locales para \[f(x) = x^5 – 5x^3.\]

Solución:

Para aplicar la prueba de la segunda derivada, primero necesitamos encontrar los puntos críticos \(c\) donde \(f′(c) = 0\). La derivada es

\[f′(x) = 5x^4 – 15x^2.\]

Por lo tanto,

\[f′(x) = 5x^4 – 15x^2 = 5x^2(x^2 – 3) = 0\]

cuando

\[x = 0, \pm\sqrt{3}.\]

Para determinar si \(f\) tiene extremos locales en alguno de estos puntos, necesitamos evaluar el signo de \(f′′\) en estos puntos. La segunda derivada es

\[f′′(x) = 20x^3 – 30x = 10x(2x^2 – 3).\]

En la siguiente tabla, evaluamos la segunda derivada en cada uno de los puntos críticos y usamos la prueba de la segunda derivada para determinar si \(f\) tiene un máximo local o un mínimo local en alguno de estos puntos.

\(x\)	\(f′′(x)\)	Conclusión
\(-\sqrt{3}\)	\(-30\sqrt{3}\)	Máximo local
\(0\)	\(0\)	La prueba de la segunda derivada no es concluyente
\(\sqrt{3}\)	\(30\sqrt{3}\)	Mínimo local

Mediante la prueba de la segunda derivada, concluimos que \(f\) tiene un máximo local en \(x = -\sqrt{3}\) y \(f\) tiene un mínimo local en \(x = \sqrt{3}\). La prueba de la segunda derivada no es concluyente en \(x = 0\). Para determinar si \(f\) tiene extremos locales en \(x = 0\), aplicamos la prueba de la primera derivada. Para evaluar el signo de \(f'(x) = 5x^2(x^2 – 3)\) para \(x \in (-\sqrt{3}, 0)\) y \(x \in (0, \sqrt{3})\), sean \(x = -1\) y \(x = 1\) los dos puntos de prueba. Dado que \(f'(-1) < 0\) y \(f'(1) < 0\), concluimos que \(f\) es decreciente en ambos intervalos y, por lo tanto, \(f\) no tiene extremos locales en \(x = 0\), como se muestra en la siguiente gráfica.

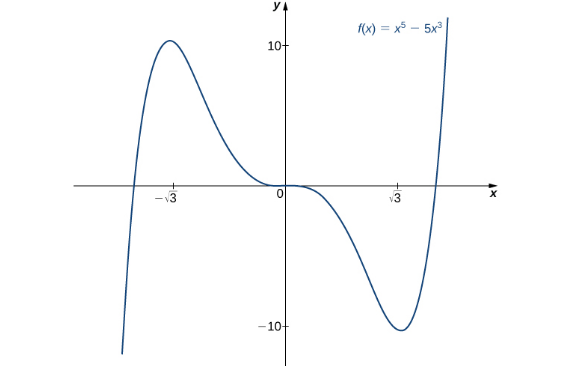
Figura 4.5.8 La función \(f\) tiene un máximo local en \(x = -\sqrt{3}\) y un mínimo local en \(x = \sqrt{3}\). ♦

Ejercicio de control 4.5.4

Considera la función \[f(x) = x^3 – \frac{3}{2}x^2 – 18x.\] Los puntos \(c = 3, -2\) satisfacen \(f'(c) = 0.\) Usa la prueba de la segunda derivada para determinar si \(f\) tiene un máximo o mínimo local en esos puntos. ♦

      Tenga en cuenta que para el caso (iii) cuando f ″(c) = 0, entonces f puede tener un máximo local, un mínimo local, o ninguno en c. Por ejemplo, las funciones f (x) = x³, f (x) = x⁴ y f (x) = − x⁴ tienen puntos críticos en x = 0. En cada caso, la segunda derivada es cero en x = 0. Sin embargo, la función f (x) = x⁴ tiene un mínimo local en x = 0, mientras que la función f (x) = − x⁴ tiene un máximo local en x, y la función f (x) = x³ no tiene un extremo local en x = 0.

Ahora hemos desarrollado las herramientas que necesitamos para determinar dónde una función está creciendo y decreciendo, así como también hemos adquirido una comprensión de la forma básica de la gráfica de una función. En la siguiente sección discutimos lo que le sucede a una función cuando x → ± ∞. En ese momento, tendremos suficientes herramientas para proporcionar gráficas precisos de una gran variedad de funciones.