| 9. Ecuaciones diferenciales | 9.11. Problemas de valores en la frontera y expansiones de Fourier |
9.11.2 Expansiones de Fourier I
En el Ejemplo 9.11.1.4 y los Ejercicios 9.11.1.19 a 9.11.1.22 vimos que las funciones propias del Problema 5 son ortogonales en [−L, L] y las funciones propias de los Problemas 1 a 4 son ortogonales en [0, L]. En esta sección y en la siguiente presentamos algunos desarrollos en serie en términos de estas funciones propias. Usaremos estas expansiones para resolver ecuaciones diferenciales parciales en el Capítulo 9.12.
Teorema 9.11.2.1
Suponga que las funciones φ1, φ2, φ3, . . ., son ortogonales en [a, b] y
(9.11.2.1)
Sean c1, c2, c3,. . . constantes tales que las sumas parciales 
satisfacen las desigualdades
|fN(x)| ≤ M, a ≤ x ≤ b, N = 1, 2, 3, . . .
para alguna constante M < ∞. Supongamos también que la serie
(9.11.2.2)
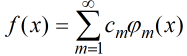
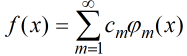
converge y es integrable en [a, b]. Entonces
(9.11.2.3) ♦
Prueba:
Multiplicando (9.11.2.2) por φn e integrando se obtiene
(9.11.2.4)
Se puede demostrar que la acotación de las sumas parciales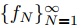 
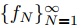
y la integrabilidad de f nos permiten intercambiar las operaciones de integración y suma a la derecha de (9.11.2.4), y reescribir (9.11.2.4) como
(9.11.2.5)
(Esto no es fácil de probar.) Dado que
(9.11.2.5) se reduce a
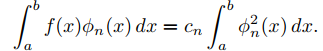
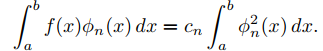
Ahora (9.11.2.1) implica (9.11.2.3). ◊
El teorema 9.11.2.1 motiva la siguiente definición.
Definición 9.11.2.2
Suponga φ1, φ2, . . . , ϕn , . . . son ortogonales en [a, b] y
. Sea f integrable en [a, b], y defina
(9.11.2.6)
Entonces la serie infinita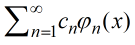 
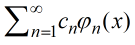
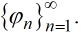
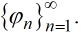
se llama desarrollo de Fourier de f en términos del conjunto ortogonal 
y c1, c2, . . . , cn , . . . se denominan coeficientes de Fourier de f con respecto a 
Indicamos la relación entre f y su expansión de Fourier por
(9.11.2.7)
Usted puede preguntarse por qué no escribimos
en lugar de (9.11.2.7). Desafortunadamente, esto no siempre es cierto. La serie de la derecha puede divergir para algunos o todos los valores de x en [a, b], o puede converger a f (x) para algunos valores de x y no para otros. Entonces, por ahora, solo pensaremos en la serie como asociada con f debido a la definición de los coeficientes {cn}, e indicaremos esta asociación informalmente como en (9.11.2.7).
Series de Fourier
Ahora estudiaremos las expansiones de Fourier en términos de las funciones propias
del Problema 5. Si f es integrable en [−L, L], su expansión de Fourier en términos de estas funciones se llama la serie de Fourier de f en [−L, L]. Ya que
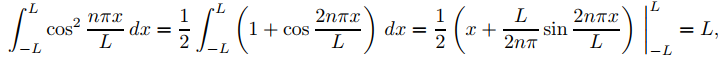
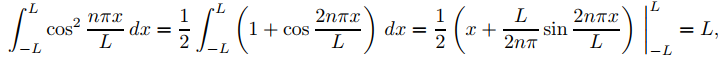
y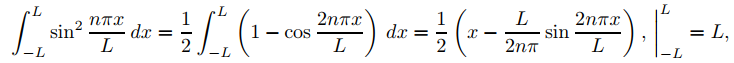
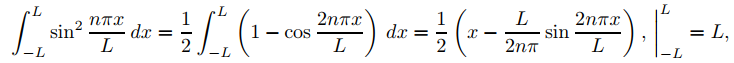
vemos de (9.11.2.6) que la serie de Fourier de f en [−L, L] es
donde
y 
Tenga en cuenta que a0 es el valor promedio de f en [−L, L], mientras que an y bn (para n ≥ 1) son el doble de los valores promedio de
y 
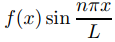
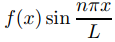
en [−L, L], respectivamente.
Convergencia de la Serie de Fourier
La cuestión de la convergencia de las series de Fourier para funciones integrables arbitrarias está más allá del alcance de este libro. Sin embargo, podemos enunciar un teorema que resuelve esta cuestión para la mayoría de las funciones que surgen en las aplicaciones.
Definición 9.11.2.3
Se dice que una función f es uniforme a trozos en [a, b] si:
(a) f tiene como máximo un número finito de puntos de discontinuidad en (a, b);
(b) f ′ existe y es continua excepto posiblemente en un número finito de puntos en (a, b);
(c) f (x0+) = 
f (x) y f ′(x0+) = f ′(x) existen si a ≤ x0 < b;
(d) f (x0−) = 
f (x) y f ′(x0−) = f ′(x) existen si a < x0 ≤ b.
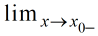
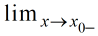
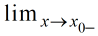
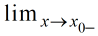
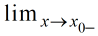
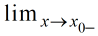
Dado que se requiere que f y f ′ sean continuas en todos menos en un número finito de puntos en [a, b], f (x0+) = f (x0−) y f ′(x0+) = f ′(x0−)) para todos excepto en un número finito de valores de x0 en (a, b). Recuerde de la Sección 9.8.1 que se dice que f tiene una discontinuidad de salto en x0 si f (x0+) ≠ f (x0−).
El siguiente teorema da condiciones suficientes para la convergencia de una serie de Fourier. La prueba está más allá del alcance de este libro.
Teorema 9.11.2.2
Si f es suave por partes en [−L, L], entonces la serie de Fourier
(9.11.2.8)
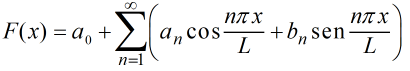
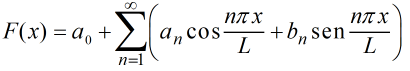
de f en [−L, L] converge para todo x en [−L, L]; es más,
♦
Como f (x+) = f (x−) si f es continua en x, también podemos decir que
Tenga en cuenta que F es en sí misma suave por partes en [−L, L], y F(x) = f (x) en todos los puntos del intervalo abierto (−L, L) donde f es continua. Dado que la serie en (9.11.2.8) converge a F(x) para todo x en [−L, L], puede verse tentado a inferir que el error
se puede hacer tan pequeño como queramos para todo x en [−L, L] eligiendo N lo suficientemente grande. Sin embargo, esto no es cierto si f tiene una discontinuidad en algún lugar de (−L, L), o si f (−L+) ≠ f (L−). Esta es la situación en este caso.
Si f tiene una discontinuidad de salto en un punto α en (−L, L), habrá secuencias de puntos {uN} y {vN} en (−L, α) y (α, L), respectivamente, tales que
y
EN(uN) ≈ 0.09 | f (α−) − f (α+)| y EN(vN) ≈ 0.09 | f (α−) − f (α+)|.
Por lo tanto, el valor máximo del error EN(x) cerca de α no tiende a cero cuando N → ∞, sino que ocurre cada vez más cerca (y en ambos lados de) α, y es esencialmente independiente de N.
Si f (−L+) ≠ f (L−), entonces habrá sucesiones de puntos {uN} y {vN} en (−L, L) tales que
EN(uN) ≈ 0.09 | f ( −L+) − f (L−)| y EN(vN) ≈ 0.09 | f ( −L+) − f (L−)|.
Este es el fenómeno de Gibbs. Habiendo sido alertado al respecto, puede verlo en las Figuras 9.11.2.2 – 9.11.2.4, a continuación; sin embargo, daremos un ejemplo específico al final de esta sección.
Ejemplo ilustrativo 9.11.2.1
Encuentre la serie de Fourier de la función suave por partes
en [−2, 2] (Figura 9.11.2.1). Determina la suma de la serie de Fourier para −2 ≤ x ≤ 2.
Solución:
Tenga en cuenta que no nos molestamos en definir f (−2), f (0) y f (2). No importa cómo se definan, f es suave por partes en [−2, 2], y los coeficientes en la serie de Fourier
no se ven afectados por ellos. En cualquier caso, el Teorema 9.11.2.2 implica que F(x) = f (x) en (−2, 0) y (0, 2), donde f es continua, mientras que
y
Para resumir,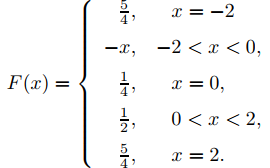
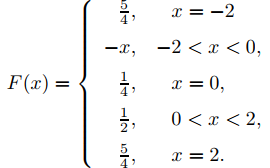
Calculamos los coeficientes de Fourier de la siguiente manera: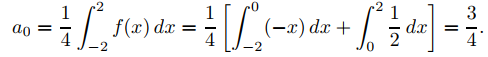
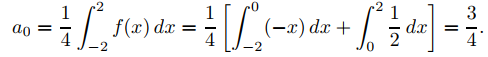
Si n ≥ 1, entonces
y
Por lo tanto
La figura 9.11.2.2 muestra cómo la suma parcial
aproxima f (x) para m = 5 (curva punteada), m = 10 (curva discontinua) y m = 15 (curva continua).
Funciones pares e impares
Calcular los coeficientes de Fourier de una función f puede ser tedioso; sin embargo, el cálculo a menudo se puede simplificar explotando las simetrías en f o en algunos de sus términos. Para centrarnos en esto, recordamos algunos conceptos que estudiaste en cálculo. Sean u y v definidos en [−L, L] y supongamos que
u(−x) = u(x) y v(−x) = −v(x), −L ≤ x ≤ L.
Entonces decimos que u es una función par y v es una función impar. Tenga en cuenta que:
- El producto de dos funciones pares es par.
- El producto de dos funciones impares es par.
- El producto de una función par y una función impar es impar.
Ejemplo ilustrativo 9.11.2.2
Las funciones u(x) = cosωx y u(x) = x2 son pares, mientras que v(x) = senωx y v(x) = x3 son impares. La función w(x) = ex no es ni par ni impar.
Aprendiste las partes (a) y (b) del siguiente teorema en cálculo, y las otras partes se derivan de ellas (Ejercicio 1).
Teorema 9.11.2.3
Suponga que u es par y v es impar en [−L, L]. Entonces:
Ejemplo ilustrativo 9.11.2.3
Encuentre la serie de Fourier de f (x) = x2 − x en [−2, 2] y determine su suma para −2 ≤ x ≤ 2.
Solución:
Como L = 2,
donde
(9.11.2.9)
(9.11.2.10)
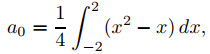
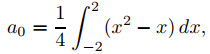
y
(9.11.2.11)
Simplificamos la evaluación de estas integrales usando el Teorema 9.11.2.3 con u(x) = x2 y v(x) = x; así, de (9.11.2.9),
De (9.11.2.10),
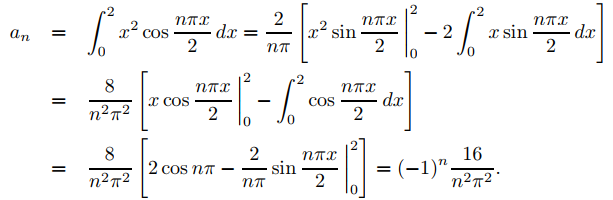
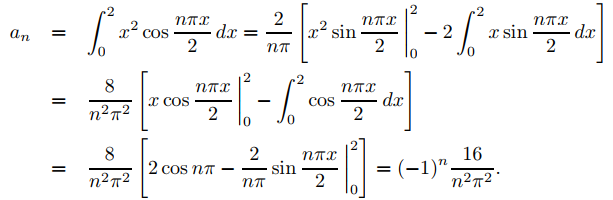
De (9.11.2.11),
Por lo tanto
El teorema 9.11.2.2 implica que
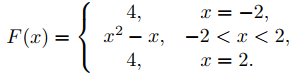
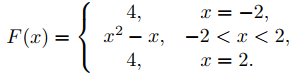
La Figura 9.11.2.3 muestra cómo la suma parcial
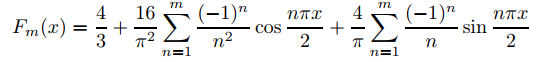
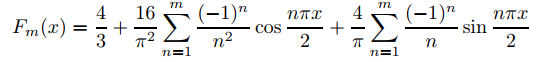
aproxima f (x) para m = 5 (curva punteada), m = 10 (curva discontinua) y m = 15 (curva continua). ♦
Figura 9.11.2.3 Aproximación de f (x) = x2 − x por sumas parciales de su serie de Fourier en [−2, 2]
El teorema 9.11.2.3 implica el siguiente teorema.
Teorema 9.11.2.4
Supongamos que f es integrable en [−L, L].
(a) Si f es par, la serie de Fourier de f en [−L, L] es
,
donde
(b) Si f es impar, la serie de Fourier de f en [−L, L] es
donde
♦
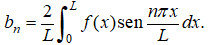
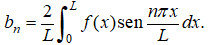
Ejemplo ilustrativo 9.11.2.4
Encuentre la serie de Fourier de f (x) = x en [−π, π] y determine su suma para −π ≤ x ≤ π.
Solución:
Como f es impar y L = π,
donde
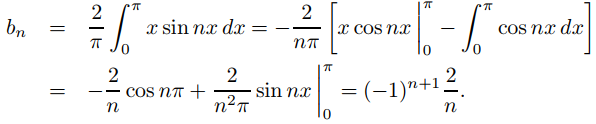
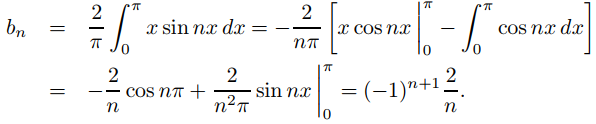
Por lo tanto
El teorema 9.11.2.2 implica que
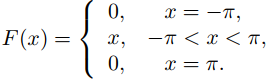
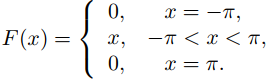
La figura 9.11.2.4 muestra cómo la suma parcial
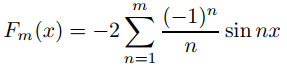
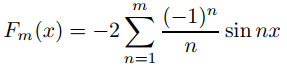
aproxima f (x) para m = 5 (curva punteada), m = 10 (curva discontinua) y m = 15 (curva sólida).
Figura 9.11.2.4 Aproximación de f (x) = x por sumas parciales de su serie de Fourier en [−π, π].
Ejemplo ilustrativo 9.11.2.5
Encuentre la serie de Fourier de f (x) = |x| en [−π, π] y determine su suma para −π ≤ x ≤ π.
Solución:
Como f es par y L = π,
Como f (x) = x si x ≥ 0,
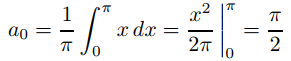
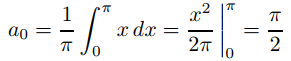
y, si n ≥ 1,
Por lo tanto
(9.11.2.12)
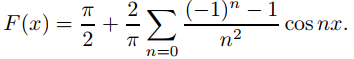
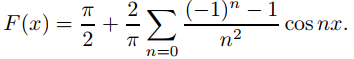
Sin embargo, como
los términos en (9.11.2.12) para los cuales n = 2m son todos ceros. Por lo tanto solo incluiremos los términos para los cuales n = 2m + 1; es decir, podemos reescribir (9.11.2.12) como
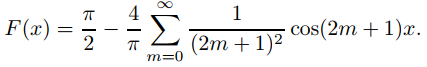
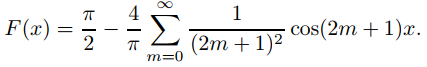
Sin embargo, dado que no importa el nombre del índice de sumatoria, preferimos reemplazar m por n, y escribir}
Como |x| es continua para todo x y | − π| = |π|, el teorema 9.11.2.2 implica que F(x) = |x| para todo x en [−π, π].
Ejemplo ilustrativo 9.11.2.6
Encuentre la serie de Fourier de f (x) = x(x2 − L2) en [−L, L] y determine su suma para −L ≤ x ≤ L.
Solución:
Como f es impar,
donde
Por lo tanto
El teorema 9.11.2.2 implica que F(x) = x(x2 − L2) para todo x en [−L, L].
Ejemplo ilustrativo 9.11.2.7 (Fenómeno de Gibbs)
La serie de Fourier de
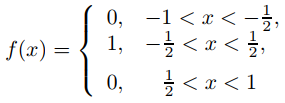
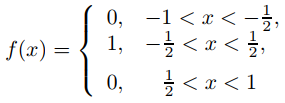
en [−1, 1] es
(Compruebe). De acuerdo con el Teorema 9.11.2.2,
por lo tanto, F (así como f) tiene discontinuidades de salto unitario en x = ±12. Las figuras 9.11.2.6 – 9.11.2.7 muestran las gráficas de y = f (x) y
para N = 10, 20 y 30. Puede ver que aunque F2N−1 se aproxima bien a F (y por lo tanto a f) en intervalos más grandes a medida que N aumenta, los valores absolutos máximos de los errores siguen siendo aproximadamente iguales a 0,09, pero ocurren más cerca a las discontinuidades x = ±12 a medida que N aumenta.
|
Figura 9.11.2.5 El fenómeno de Gibbs: Ejemplo 9.11.2.7, N = 10 |
Figura 9.11.2.6 El fenómeno de Gibbs: Ejemplo 9.11.2.7, N = 20 |
Figura 9.11.2.7 El fenómeno de Gibbs: Ejemplo 9.11.2.7, N = 30 |
USO DE TECNOLOGÍA
El cálculo de los coeficientes de Fourier será tedioso en muchos de los ejercicios de este capítulo y del siguiente. Para aprender la técnica, le recomendamos que haga algunos ejercicios en cada sección “a mano”, quizás usando la tabla de integrales al principio del libro. Sin embargo, lo alentamos a usar su software favorito de cálculo simbólico en los problemas más difíciles.