| 11. Diferenciación de funciones de varias variables |
11.1 Funciones de varias variables
Objetivos de aprendizaje
- 9.1.1 Reconocer una función de dos variables e identificar su dominio y rango.
- 9.1.2 Dibujar una gráfica de una función de dos variables.
- 9.1.3 Dibujar varios trazos o curvas de nivel de una función de dos variables.
- 9.1.4 Reconocer una función de tres o más variables e identificar sus superficies de nivel.
Nuestro primer paso es explicar qué es una función de más de una variable, comenzando con funciones de dos variables independientes. Este paso incluye identificar el dominio y rango de tales funciones y aprender a graficarlas. También examinamos formas de relacionar las gráficas de funciones en tres dimensiones con las gráficas de funciones planas más familiares.
Funciones de dos variables
La definición de una función de dos variables es muy similar a la definición de una función de una variable. La principal diferencia es que, en lugar de asignar valores de una variable a los valores de otra variable, asignamos pares ordenados de variables a otra variable.
DEFINICIÓN
Una función de dos variables z = f (x, y) mapea cada par ordenado (x, y) en un subconjunto D del plano real ℝ2 a un número real único z. El conjunto D se llama dominio de la función. El rango de f es el conjunto de todos los números reales z que tiene al menos un par ordenado (x, y) ∈ D tal que f (x, y) = z como se muestra en la siguiente figura. ♦

Determinar el dominio de una función de dos variables implica tener en cuenta las restricciones de dominio que puedan existir. Veamos el siguiente ejemplo.
Ejemplo ilustrativo 11.1.1: Dominios y rangos para funciones de dos variables
Encuentre el dominio y rango de cada una de las siguientes funciones:
a. f (x, y) = 3x + 5y + 2
b. g(x, y) = √(9 − x2 − y2)
Solución:
a. Este es un ejemplo de una función lineal en dos variables. No hay valores o combinaciones de x e y que causen que f (x, y) no esté definida, por lo que el dominio de f es R2. Para determinar el rango, primero elija un valor para z. Necesitamos encontrar una solución a la ecuación f (x, y) = z, o 3x + 5y + 2 = z. Una de estas soluciones se puede obtener estableciendo primero y = 0, lo que da como resultado la ecuación 3x + 2 = z. La solución a esta ecuación es x = (z − 2)/3, lo que da el par ordenado ((z − 2)/3, 0) como una solución a la ecuación f (x, y) = z para cualquier valor de z. Por lo tanto, el rango de la función es todos los números reales, o R.
b. Para que la función g(x, y) tenga un valor real, la cantidad debajo de la raíz cuadrada debe ser no negativa:
9 − x2 − y2 ≥ 0.
Esta desigualdad se puede escribir en la forma
x2 + y2 ≤ 9.
Por lo tanto, el dominio de g(x, y) es {(x, y) ∈ ℝ2 | x2 + y2 ≤ 9}. La gráfica de este conjunto de puntos se puede describir como un disco de radio 3 centrado en el origen. El dominio incluye el círculo límite como se muestra en el siguiente gráfico.
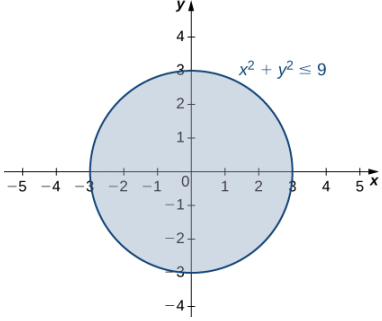
(Figura 11.1.2 El dominio de la función g(x, y) = √ (9 − x2 − y2) es un disco cerrado de radio 3.)
Para determinar el rango de g(x, y) = √(9 − x2 − y2) comenzamos con un punto (x0, y0) en el perímetro del dominio, que está definido por la relación x2 + y2 = 9. De ello se deduce que x02 + y02 = 9 y

Si x02 + y02 = 0 (en otras palabras, x0 = y0 = 0), entonces

Este es el valor máximo de la función. Dado cualquier valor c entre 0 y 3, podemos encontrar un conjunto completo de puntos dentro del dominio de g tal que g(x, y) = c:

Dado que 9 − c2 > 0, esto describe un círculo de radio √(9 − c2) centrado en el origen. Cualquier punto de este círculo satisface la ecuación g(x, y) = c. Por lo tanto, el rango de esta función se puede escribir en notación de intervalo como [0, 3]. ♦
Ejercicio de control 11.1.1
Encuentre el dominio y rango de la función f (x, y) = √(36 − 9x2 − 9y2). ♦
Graficas de funciones de dos variables
Suponga que deseamos graficar la función z = (x, y). Esta función tiene dos variables independientes (x e y) y una variable dependiente (z). Al graficar una función y = f (x) de una variable, usamos el plano cartesiano. Podemos graficar cualquier par ordenado (x, y) en el plano, y cada punto en el plano tiene asociado un par ordenado (x, y). Con una función de dos variables, cada par ordenado (x, y) en el dominio de la función se asigna a un número real z. Por tanto, la gráfica de la función f consta de triples ordenados de números (x, y, z). La gráfica de una función z = (x, y) de dos variables se llama superficie.
Para comprender más completamente el concepto de graficar un conjunto de triples ordenados para obtener una superficie en un espacio tridimensional, imagine el sistema de coordenadas (x, y), el plano xy. Entonces, cada punto en el dominio de la función f tiene un valor z único asociado. Si z es positivo, entonces el punto graficado está ubicado por encima del plano xy, si z es negativo, entonces el punto graficado está ubicado debajo del plano xy. El conjunto de todos los puntos graficados se convierte en la superficie bidimensional que es la gráfica de la función f.
Ejemplo ilustrativo 11.1.2: Graficar funciones de dos variables
Cree una gráfica de cada una de las siguientes funciones:
a. g(x, y) = √(9 − x2 − y2)
b. f (x, y) = x2 + y2
Solución:
a. En el Ejemplo ilustrativo 11.1.1, determinamos que el dominio de g(x, y) = √(9 − x2 − y2) es {(x, y) ∈ ℝ2 | x2 + y2 ≤ 9} y el rango es {z ∈ ℝ | 0 ≤ z ≤ 3}. Cuando x2 + y2 = 9 tenemos g(x, y) = 0. Por lo tanto, cualquier punto en el círculo de radio 3 centrado en el origen en el plano xy se asigna a z = 0 en ℝ3. Si x2 + y2 = 8, entonces g(x, y) = 1, entonces cualquier punto en el círculo de radio 2√2 centrado en el origen en el plano xy se corresponde con z = 1 en ℝ3. A medida que x2 + y2 se aproxima a cero, el valor de z se aproxima a 3. Cuando x2 + y2 = 0, entonces g(x, y) = 3. Este es el origen en el plano xy. Si x2 + y2 es igual a cualquier otro valor entre 0 y 9, entonces g(x, y) es igual a alguna otra constante entre 0 y 3. La superficie descrita por esta función es un hemisferio centrado en el origen con radio 3 como se muestra en el siguiente gráfico

(Figura 11.1.3 Gráfico del hemisferio representado por la función dada de dos variables.)
b. Esta función también contiene la expresión x2 + y2. Al igualar esta expresión a varios valores a partir de cero, obtenemos círculos de radio creciente. El valor mínimo de f (x, y) = x2 + y2 es cero (obtenido cuando x = y = 0.). Cuando x = 0, la función se convierte en z = y2, y cuando y = 0, entonces la función se convierte en z = x2. Estas son secciones transversales del gráfico y son parábolas. Recuerde de Introducción a los vectores en el espacio que el nombre de la gráfica de f (x, y) = x2 + y2 es un paraboloide. La gráfica de f aparece en la siguiente figura.

(Figura 9.1.4 Un paraboloide es la gráfica de la función dada de dos variables).
Ejemplo ilustrativo 11.1.3: Tuercas y tornillos
Una función de beneficio para un fabricante de hardware viene dada por
f (x, y) = 16 − (x − 3)2 − (y − 2)2,
donde x es el número de tuercas vendidas por mes (medido en miles) e y representa el número de tornillos vendidos por mes (medido en miles). La ganancia se mide en miles de dólares. Dibuja una gráfica de esta función.
Solución:
Esta función es una función polinomial en dos variables. El dominio de f consta de pares de coordenadas (x, y) que producen una ganancia no negativa:
16 − (x − 3)2 − (y − 2)2 ≥ 0
(x − 3)2 + (y − 2)2 ≤ 16.
Este es un disco de radio 4 centrado en (3, 2). Una restricción adicional es que ambos x e y deben ser no negativos. Cuando x = 3 y y = 2, f (x, y) = 16. Tenga en cuenta que es posible que cualquiera de los valores no sea un número entero; por ejemplo, es posible vender 2.5 mil tuercas en un mes. El dominio, por lo tanto, contiene miles de puntos, por lo que podemos considerar todos los puntos dentro del disco. Para cualquier z < 16, podemos resolver la ecuación f (x, y) = z:
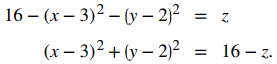
Como z < 16, sabemos que 16 − z > 0, por lo que la ecuación anterior describe un círculo con radio √(16 − z) centrado en el punto (3, 2). Por lo tanto. el rango de f (x, y) es {z ∈ R | z ≤ 16}. La gráfica de f (x, y) también es un paraboloide, y este paraboloide apunta hacia abajo como se muestra en la siguiente imagen.

(Figura 11.1.5 La gráfica de la función dada de dos variables también es un paraboloide).
Curvas de nivel
Si los excursionistas caminan por senderos escarpados, pueden usar un mapa topográfico que muestre cuán abruptamente cambian los senderos. Un mapa topográfico contiene líneas curvas llamadas curvas de nivel. Cada línea de contorno corresponde a los puntos del mapa que tienen la misma elevación (Figura 11.1.6). Una curva de nivel de una función de dos variables f (x, y) es completamente análoga a una línea de contorno en un mapa topográfico.
 |
 |
(Figura 11.1.6 (a) Un mapa topográfico de Devil’s Tower, Wyoming. Las líneas que están juntas indican un terreno muy empinado. (B) Una foto en perspectiva de Devil’s Tower muestra cuán empinados son sus lados. Observe la parte superior de la torre tiene la misma forma que el centro del mapa topográfico.)
DEFINICIÓN
Dada una función f (x, y) y un número c en el rango de f, una curva de nivel de una función de dos variables para el valor c se define como el conjunto de puntos que satisfacen la ecuación f (x, y) = c. ♦
Volviendo a la función g(x, y) = √(9 − x2 − y2), podemos determinar las curvas de nivel de esta función. El rango de g es el intervalo cerrado [0, 3]. Primero, elegimos cualquier número en este intervalo cerrado, digamos, c = 2. La curva de nivel correspondiente a c = 2 se describe mediante la ecuación
√(9 − x2 − y2) = 2
Para simplificar, elevamos al cuadrado ambos lados de esta ecuación:
9 − x2 − y2 = 4
Ahora, multiplica ambos lados de la ecuación por −1 y suma 9 a cada lado:
x2 + y2 = 5
Esta ecuación describe un círculo centrado en el origen con radio √5. El uso de valores de c entre 0 y 3 produce otros círculos también centrados en el origen. Si c = 3, entonces el círculo tiene radio 0, por lo que consta únicamente del origen. La figura 11.1.7 es una gráfica de las curvas de nivel de esta función correspondientes a c = 0,1,2 y 3. Tenga en cuenta que en la deducción anterior es posible que hayamos introducido soluciones adicionales elevando ambos lados al cuadrado. Este no es el caso aquí porque el rango de la función raíz cuadrada no es negativo.
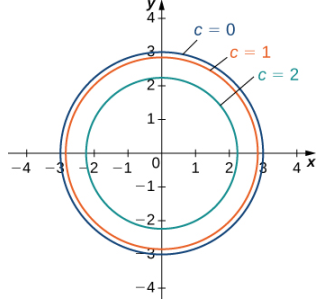
(Figura 11.1.7 Curvas de nivel de la función g(x, y) = √(9 − x2 − y2) = 2, usando c = 0,1,2, y 3 (c = 3 corresponde al origen).)
Ejemplo ilustrativo 11.1.4: Hacer un mapa de contorno
Dada la función f (x, y) = √(8 + 8x − 4y − 4x2 − y2), encuentre la curva de nivel correspondiente a c = 0. Luego cree un mapa de contorno para esta función. ¿Cuáles son el dominio y el rango de f ?
Solución:
Para encontrar la curva de nivel para c = 0, establecemos f (x, y) = 0 y resolvemos. Esto da
0 = √(8 + 8x − 4y − 4x2 − y2).
Luego cuadramos ambos lados y multiplicamos ambos miembros de la ecuación por −1:
4x2 + y2 − 8x + 4y − 8 = 0.
Ahora, reorganizamos los términos, reuniendo los términos x y los términos y, y sumamos 8 a cada lado:
4x2 − 8x + y2 + 4y = 8.
A continuación, agrupamos los pares de términos que contienen la misma variable entre paréntesis y sacamos factor común 4 del primer par:
4 (x2 − 2x) + (y2 + 4y) = 8.
Luego completamos el cuadrado en cada par de paréntesis y agregamos el valor correcto en el lado derecho:
4(x2 − 2x + 1) + (y2 + 4y + 4) = 8 + 4 (1) + 4.
A continuación, factorizamos el lado izquierdo y simplificamos el lado derecho:
4 (x − 1)2+ (y + 2)2 = 16.
Por último, dividimos ambos lados entre 16:
 (11.1.1)
(11.1.1)
Esta ecuación describe una elipse centrada en (1, −2). La gráfica de esta elipse aparece en la siguiente imagen.
 (Figura 11.1.8 Curva de nivel de la función f (x, y) = √(8 + 8x − 4y − 4x2 − y2) correspondiente a c = 0.)
(Figura 11.1.8 Curva de nivel de la función f (x, y) = √(8 + 8x − 4y − 4x2 − y2) correspondiente a c = 0.)
Podemos repetir la misma derivación para valores de c menores que 4. Entonces, la ecuación 11.1.1 se convierte en
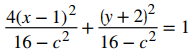
para un valor arbitrario de c. La figura 11.1.9 muestra un mapa de contorno para f (x, y) usando los valores c = 0, 1, 2 y 3. Cuando c = 4, la curva de nivel es el punto (−1, 2).
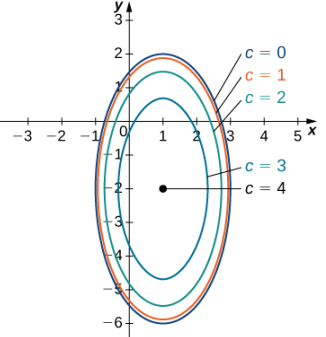
(Figura 11.1.9 Mapa de contorno para la función f (x, y) = √(8 + 8x − 4y − 4x2 − y2) usando los valores c = 0, 1, 2, 3 y 4)
Ejercicio de control 11.1.2
Encuentre y grafique la curva de nivel de la función g(x, y) = x2 + y2 − 6x + 2y correspondiente a c = 15.
Otra herramienta útil para comprender la gráfica de una función de dos variables se llama trazo vertical. Las curvas de nivel siempre se grafican en el plano xy, pero como su nombre lo indica, las trazas verticales se grafican en los planos xz o yz.
DEFINICIÓN Traza vertical
Considere una función z = f (x, y) con dominio D ⊆ R2. Una traza vertical de la función puede ser el conjunto de puntos que resuelve la ecuación f (a, y) = z para una constante dada x = a o f (x, b) = z para una constante dada y = b. ♦
Ejemplo ilustrativo 11.1.5: Encontrar trazas verticales
Encuentre trazos verticales para la función f (x, y) = senx cosy correspondiente a x = −π/4, 0, / y / π / 4, e y = −π/4, 0, y π/4.
Solución:
Primero establezca x = −π/4 en la ecuación z = senx cosy:

Esto describe una gráfica de coseno en el plano x = −π/4. Los otros valores de z aparecen en la siguiente tabla.

Tabla 11.1.1 Trazas verticales paralelos al plano xz para la función f (x, y) = senx cosy
De manera similar, podemos sustituir los valores de y en la ecuación f (x, y) para obtener las trazas en el plano yz, como se muestra en la siguiente tabla.

Tabla 11.1.2 Trazas verticales paralelos al plano yz para la función f (x, y) = senx cosy
Las tres trazas en el plano xz son funciones coseno; las tres trazas en el plano yz son funciones sinusoidales. Estas curvas aparecen en las intersecciones de la superficie con los planos x = −π/4, x = 0, x = π/4 e y = −π/4, y = 0, y = π/4 como se muestra en la siguiente figura.

Trazas en el plano xz
(a)
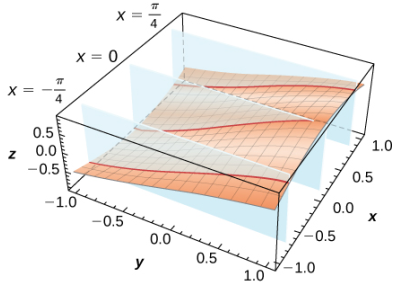
Trazas en el plano yz
(b)
(Figura 11.1.10 Las trazas verticales de la función f (x, y) = senx cosy son curvas coseno en los planos xz (a) y curvas sinusoidales en los planos yz (b).)
Ejercicio de control 11.1.3
Determine la ecuación de la traza vertical de la función g (x, y) = −x2 − y2 + 2x + 4y − 1 correspondiente a y = 3, y describa su gráfica.
Las funciones de dos variables pueden producir algunas superficies de aspecto llamativo. La siguiente figura muestra dos ejemplos.


(Figura 11.1.11 Ejemplos de superficies que representan funciones de dos variables: (a) una combinación de una función de potencia y una función de seno y (b) una combinación de funciones trigonométricas, exponenciales y logarítmicas.)
Funciones de más de dos variables
Hasta ahora, hemos examinado solo funciones de dos variables. Sin embargo, es útil echar un vistazo breve a las funciones de más de dos variables. Dos de esos ejemplos son
f (x, y, z) = x2 − 2xy + y2 + 3yz − z2 + 4x − 2y + 3x − 6 (un polinomio en tres variables)
y
g (x, y, t) = (x2 − 4xy + y2) sent − (3x + 5y) cost.
En la primera función, (x, y, z) representa un punto en el espacio, y la función f asigna cada punto en el espacio a una cuarta cantidad, como la temperatura o la velocidad del viento. En la segunda función, (x, y) puede representar un punto en el plano y t puede representar el tiempo. La función podría asignar un punto en el plano a una tercera cantidad (por ejemplo, presión) en un tiempo t dado. El método para encontrar el dominio de una función de más de dos variables es análogo al método para funciones de una o dos variables.
Ejemplo ilustrativo 11.1.6: Dominios para funciones de tres variables
Encuentre el dominio de cada una de las siguientes funciones:
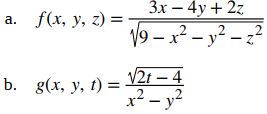
Solución:
a. Para la función  para ser definida (y ser un valor real), se deben cumplir dos condiciones:
para ser definida (y ser un valor real), se deben cumplir dos condiciones:
- El denominador no puede ser cero.
- El radicando no puede ser negativo.
La combinación de estas condiciones conduce a la desigualdad
9 − x2 − y2 − z2 > 0.
Pasar las variables al otro lado y revertir la desigualdad da el dominio como
dominio ( f ) = {(x, y, z) ∈ R3∣ x2 + y2 + z2 < 9},
que describe una esfera de radio 3 centrada en el origen. (Nota: la superficie de la esfera no se incluye en este dominio).
b. Para la función  para ser definida (y ser un valor real), se deben cumplir dos condiciones:
para ser definida (y ser un valor real), se deben cumplir dos condiciones:
- El radicando no puede ser negativo.
- El denominador no puede ser cero.
Dado que el radicando no puede ser negativo, esto implica 2t − 4 ≥ 0 y, por lo tanto, t ≥ 2. Dado que el denominador no puede ser cero, x2 − y2 ≠ 0, o x2 ≠ y2, que se puede reescribir como y ≠ ± x, que son las ecuaciones de dos rectas que pasan por el origen. Por tanto, el dominio de g es
dominio (g) = {(x, y, t) | y ≠ ± x, t ≥ 2}.
Ejercicio de control 11.1.4
Encuentra el dominio de la función 
Las funciones de dos variables tienen curvas de nivel, que se muestran como curvas en el plano xy. Sin embargo, cuando la función tiene tres variables, las curvas se convierten en superficies, por lo que podemos definir superficies de nivel para funciones de tres variables.
DEFINICIÓN
Dada una función f (x, y, z) y un número c en el rango de f, una superficie de nivel de una función de tres variables se define como el conjunto de puntos que satisfacen la ecuación f (x, y, z) = c. ♦
Ejemplo ilustrativo 11.1.7: Encontrar una superficie de nivel
Encuentre la superficie de nivel para la función f (x, y, z) = 4x2 + 9y2 − z2 correspondiente a c = 1.
Solución:
La superficie de nivel está definida por la ecuación 4x2 + 9y2 − z2. Esta ecuación describe un hiperboloide de una hoja como se muestra en la siguiente figura.

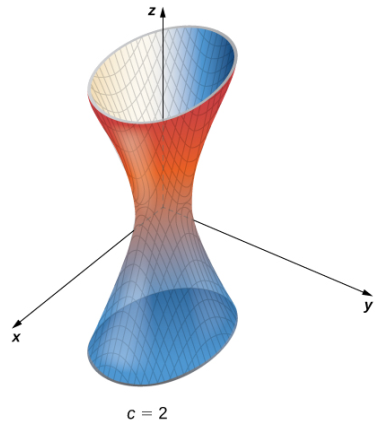


(Figura 11.1.12 Un hiperboloide de una hoja con algunas de sus superficies niveladas).
Ejercicio de control 11.1.5
Encuentra la ecuación de la superficie de nivel de la función
g (x, y, z) = x2 + y2 + z2 − 2x + 4y − 6z
correspondiente a c = 2, y describa la superficie, si es posible.
← 11. Diferenciación de funciones de varias variables | Ejercicios propuestos para el Capítulo 11.1 →
