| 9. Ecuaciones diferenciales |
9.4. Aplicaciones de ecuaciones de primer orden
EN ESTE CAPÍTULO consideramos aplicaciones de ecuaciones diferenciales de primer orden.
LA SECCIÓN 9.4.1 comienza con una discusión sobre el crecimiento y la disminución exponenciales, que probablemente ya haya visto en cálculo. Consideramos aplicaciones a la descomposición radiactiva, la datación por carbono y el interés compuesto. También consideramos problemas más complicados en los que la tasa de cambio de una cantidad es en parte proporcional a la magnitud de la cantidad, pero también está influenciada por otros factores, por ejemplo, una sustancia radiactiva se fabrica a una cierta tasa, pero se desintegra a una tasa proporcional a su masa, o un ahorrador hace depósitos regulares en una cuenta de ahorros que genera interés compuesto.
LA SECCIÓN 9.4.2 trata de las aplicaciones de la ley de enfriamiento de Newton y de los problemas de mezclas.
LA SECCIÓN 9.4.3 analiza las aplicaciones a la mecánica elemental que involucran la segunda ley del movimiento de Newton. Los problemas considerados incluyen el movimiento bajo la influencia de la gravedad en un medio resistivo y la determinación de la velocidad inicial requerida para lanzar un satélite.
LA SECCIÓN 9.4.4 trata sobre los métodos para manejar un tipo de ecuación de segundo orden que a menudo surge en las aplicaciones de la segunda ley del movimiento de Newton, reformulándola como una ecuación de primer orden con una variable independiente diferente. Aunque el método no suele conducir a una solución explícita de la ecuación dada, proporciona información valiosa sobre el comportamiento de las soluciones.
LA SECCIÓN 9.4.5 trata de las aplicaciones de las ecuaciones diferenciales a las curvas.
9.4.1 CRECIMIENTO Y DECRECIMIENTO
Dado que las aplicaciones en esta sección tratan con funciones de tiempo, denotaremos la variable independiente por t. Si Q es función de t, Q′ denotará la derivada de Q con respecto a t; de este modo,

Crecimiento y decaimiento exponencial
Uno de los modelos matemáticos más comunes para un proceso físico es el modelo exponencial, donde se supone que la tasa de cambio de una cantidad Q es proporcional a Q; de este modo
Q′ = aQ, (9.4.1.1)
donde a es la constante de proporcionalidad.
Del Ejemplo 3, la solución general de (9.4.1.1) es
Q = ceat
y la solución del problema de valor inicial
Q′ = aQ, Q(t0) = Q0
es
Q = Q0ea(t − t0) (9.4.1.2)
Como las soluciones de Q′ = aQ son funciones exponenciales, decimos que una cantidad Q que satisface esta ecuación crece exponencialmente si a > 0, o decae exponencialmente si a < 0 (Figura 9.4.1.1).

Desintegración radioactiva
La evidencia experimental muestra que el material radiactivo se desintegra a un ritmo proporcional a la masa del material presente. De acuerdo con este modelo, la masa Q(t) de un material radiactivo presente en el tiempo t satisface (9.4.1.1), donde a es una constante negativa cuyo valor para cualquier material dado debe determinarse mediante observación experimental. Para simplificar, reemplazaremos la constante negativa a por −k, donde k es un número positivo que llamaremos la constante de descomposición del material. Así, (9.4.1.1) se convierte en
Q′ = −kQ
Si la masa del material presente en t = t0 es Q0, la masa presente en el tiempo t es la solución de
Q′ = −kQ, Q(t0) = Q0
De (9.4.1.2) con a = −k, la solución de este problema de valor inicial es
Q = Q0e−k(t − t0) (9.4.1.3)
La vida media τ de un material radiactivo se define como el tiempo necesario para que se desintegre la mitad de su masa; es decir, si Q(t0) = Q0, entonces


De (9.4.1.3) con t = τ + t0, (9.4.1.4) es equivalente a
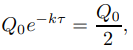
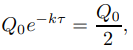
así que


Tomando logaritmos, se tiene que


entonces la vida media es
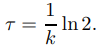
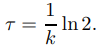
(Figura 9.4.1.2). La vida media es independiente de t0 y Q0, ya que está determinada por las propiedades del material, no por la cantidad del material presente en un momento determinado.


Ejemplo ilustrativo 9.4.1.1
Una sustancia radiactiva tiene una vida media de 1620 años.
(a) Si su masa ahora es de 4 g (gramos), ¿cuánto quedará dentro de 810 años?
(b) Encuentre el tiempo t1 cuando quedan 1,5 g de la sustancia.
Solución:
(a) De (9.4.1.3) con t0 = 0 y Q0 = 4,
Q = 4e−kt , (9.4.1.6)
donde determinamos k de (9.4.1.5), con τ = 1620 años:
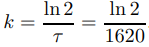
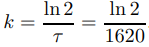
Sustituyendo esto en (9.4.1.6) se obtiene
Q = 4e−(t ln2)/1620 (9.4.1.7)
Por lo tanto, la masa que queda después de 810 años será


(b) Al establecer t = t1 en (9.4.1.7) y requerir que Q(t1) = 1.5 se obtiene


Dividiendo por 4 y tomando logaritmos se obtiene
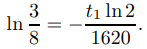
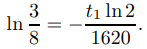
Como ln 3/8 = − ln 8/3,


Interés compuesto continuamente
Supongamos que depositamos una cantidad de dinero Q0 en una cuenta que devenga intereses y no hacemos más depósitos ni retiros durante t años, durante los cuales la cuenta devenga intereses a una tasa anual constante r. Para calcular el valor de la cuenta al final de t años, necesitamos un dato más: cómo se suma el interés a la cuenta o, como dicen los banqueros, cómo se capitaliza. Si el interés se capitaliza anualmente, el valor de la cuenta se multiplica por 1 + r al final de cada año. Esto significa que después de t años el valor de la cuenta es
Q(t) = Q0(1 + r)t.
Si el interés se capitaliza semestralmente, el valor de la cuenta se multiplica por (1 + r/2) cada 6 meses. Como esto ocurre dos veces al año, el valor de la cuenta después de t años es
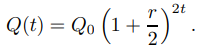
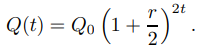
En general, si el interés se capitaliza n veces al año, el valor de la cuenta se multiplica n veces al año por (1 + r/n); por lo tanto, el valor de la cuenta después de t años es
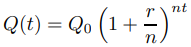
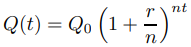
Por lo tanto, aumentar la frecuencia de capitalización aumenta el valor de la cuenta después de un período de tiempo fijo. La tabla 9.4.1.7 muestra el efecto de aumentar el número de capitalizaciones durante t = 5 años sobre un depósito inicial de Q0 = 100 (dólares), a una tasa de interés anual del 6%.
Tabla 9.4.1.7: El efecto del interés compuesto


Puede ver en la Tabla 9.4.1.7 que el valor de la cuenta después de 5 años es una función creciente de n. Ahora suponga que la tasa de interés máxima permitida en las cuentas de ahorro está restringida por ley, pero los intervalos de tiempo entre capitalizaciones sucesivas no lo están; entonces los bancos competidores pueden atraer a los ahorradores al capitalizar con frecuencia. El último paso en esta dirección es la composición continua, por lo que queremos decir que n → ∞ en (9.4.1.8). Como sabemos por cálculo que
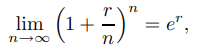
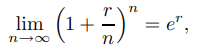
esto produce


Observe que Q = Q0ert es la solución del problema de valor inicial
Q′ = rQ, Q(0) = Q0;
es decir, con capitalización continua el valor de la cuenta crece exponencialmente.
Ejemplo ilustrativo 9.4.1.2
Si se depositan $150 en un banco que paga 5½% de interés anual compuesto continuamente, el valor de la cuenta después de t años es
Q(t) = 150e.055t
dólares (Tenga en cuenta que es necesario escribir la tasa de interés como un decimal; por lo tanto, r = .055). Por lo tanto, después de t = 10 años, el valor de la cuenta es
Q(10) = 150e.55 ≈ $259.99.
Ejemplo ilustrativo 9.4.1.3
Deseamos acumular $10 000 en 10 años haciendo un solo depósito en una cuenta de ahorros con un interés anual del 5½% compuesto continuamente. ¿Cuánto debemos depositar en la cuenta?
Solución:
El valor de la cuenta en el tiempo t es
Q(t) = Q0e.055t (9.4.1.9)
Como queremos que Q(10) sea $10 000, el depósito inicial Q0 debe satisfacer la ecuación
10000 = Q0e.55, (9.4.1.10)
obtenido al establecer t = 10 y Q(10) = 10000 en (9.4.1.9). Resolviendo (9.4.1.10) para Q0 se obtiene
Q0 = 10000e−.55 ≈ $5769.50
Crecimiento y decadencia combinados
Ejemplo ilustrativo 9.4.1.4
Una sustancia radiactiva con constante de desintegración k se produce a una tasa constante de unidades de masa por unidad de tiempo.
(a) Suponiendo que Q(0) = Q0, encuentre la masa Q(t) de la sustancia presente en el tiempo t.
(b) Encuentre límt→∞ Q(t).
Solución:
(a) Aquí
Q′ = tasa de aumento de Q − tasa de disminución de Q.
La tasa de aumento es la constante a. Dado que Q es radiactivo con constante de decaimiento k, la tasa de decrecimiento es kQ. Por lo tanto
Q′ = a − kQ.
Esta es una ecuación diferencial lineal de primer orden. Reescribiéndolo e imponiendo la condición inicial se muestra que Q es la solución del problema de valor inicial
Q′ + kQ = a, Q(0) = Q0. (9.4.1.11)
Dado que e−kt es una solución de la ecuación complementaria, las soluciones de (9.4.1.11) son de la forma Q = ue−kt, donde u′e−kt = a, entonces u′ = aekt. Por eso,


y


Dado que Q(0) = Q0, establecer t = 0 aquí produce


Por lo tanto


(b) Dado que k > 0, limt→∞ e−kt = 0, entonces de (9.4.1.12)
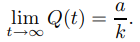
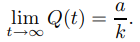
Este límite depende solo de a y k, y no de Q0. Decimos que a/k es el valor de estado estacionario de Q. De (9.4.1.12) también vemos que Q se acerca a su valor de estado estacionario desde arriba si Q0 > a/k, o desde abajo si Q0 < a/k. Si Q0 = a/k, entonces Q permanece constante (Figura 9.4.1.3).


Datación por carbono
El hecho de que Q se acerque a un valor de estado estacionario en la situación discutida en el Ejemplo 9.4.1.4 subyace al método de datación por carbono, ideado por el químico estadounidense y ganador del Premio Nobel W.S. Libby.
El carbono 12 es estable, pero el carbono 14, que se produce por el bombardeo cósmico de nitrógeno en la atmósfera superior, es radiactivo con una vida media de unos 5570 años. Libby supuso que la cantidad de carbono12 en la atmósfera ha sido constante a lo largo del tiempo y que la cantidad de carbono-14 radiactivo alcanzó su valor de estado estacionario hace mucho tiempo como resultado de su creación y descomposición durante millones de años. Estas suposiciones llevaron a Libby a concluir que la proporción de carbono-14 a carbono-12 ha sido casi constante durante mucho tiempo. Esta constante, que denotamos por R, ha sido determinada experimentalmente.
Las células vivas absorben tanto el carbono 12 como el carbono 14 en la proporción en que están presentes en el medio ambiente. Por lo tanto, la proporción de carbono-14 a carbono-12 en una célula viva siempre es R. Sin embargo, cuando la célula muere, deja de absorber carbono y la proporción de carbono-14 a carbono-12 disminuye exponencialmente a medida que el carbono-14 radiactivo decae. Esta es la base del método de datación por carbono, como se ilustra en el siguiente ejemplo.
Ejemplo ilustrativo 9.4.1.5
Un arqueólogo que investiga el sitio de un antiguo pueblo encuentra un cementerio donde la cantidad de carbono-14 presente en los restos individuales es de entre el 42 y el 44 % de la cantidad presente en los individuos vivos. Estima la edad de la aldea y el tiempo que sobrevivió.
Solución:
Sea Q = Q(t) la cantidad de carbono-14 en un conjunto individual de restos t años después de la muerte, y sea Q0 la cantidad que estaría presente en los individuos vivos. Dado que el carbono-14 se desintegra exponencialmente con una vida media de 5570 años, su constante de desintegración es
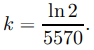
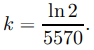
Por lo tanto
Q = Q0e−t(ln 2)/5570
si elegimos nuestra escala de tiempo para que t0 = 0 sea el momento de la muerte. Si conocemos el valor presente de Q podemos resolver esta ecuación para t, el número de años desde que ocurrió la muerte. Esto produce


Se da que Q = 0.42Q0 en restos de individuos que fallecieron primero. Por lo tanto, estas muertes ocurrieron alrededor de


años antes. Para las muertes más recientes, Q = 0.44Q0; por lo tanto, estas muertes ocurrieron alrededor de


años antes. Por lo tanto, es razonable concluir que el pueblo se fundó hace unos 7000 años y duró unos 400 años.
Un programa de ahorro
Ejemplo ilustrativo 9.4.1.6
Una persona abre una cuenta de ahorros con un depósito inicial de $1000 y posteriormente deposita $50 por semana. Encuentre el valor Q(t) de la cuenta en el tiempo t > 0, suponiendo que el banco paga 6% de interés compuesto continuamente.
Solución:
Observe que Q no es continuo, ya que hay 52 depósitos discretos por año de $50 cada uno. Para construir un modelo matemático para este problema en forma de ecuación diferencial, hacemos la suposición simplificada de que los depósitos se realizan continuamente a una tasa de $2600 por año. Esto es esencial, ya que las soluciones de ecuaciones diferenciales son funciones continuas. Con esta suposición, Q aumenta continuamente a la tasa
Q′ = 2600 + 0.06Q
y por lo tanto Q satisface la ecuación diferencial
Q′ − 0.06Q = 2600. (9.4.1.13)
(Por supuesto, debemos reconocer que la solución de esta ecuación es una aproximación al verdadero valor de Q en un momento dado. Discutiremos esto más adelante). Como e.06t es una solución de la ecuación complementaria, las soluciones de (9.4.1.13) son de la forma Q = ue.06t, donde u′e.06t = 2600. Por lo tanto, u′ = 2600e−.06t,


y
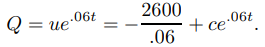
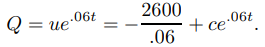
Establecer t = 0 y Q = 1000 aquí produce


y al sustituir esto en (9.4.1.14) se obtiene


donde el primer término es el valor debido al depósito inicial y el segundo es debido a los depósitos semanales posteriores. ♦
Se debe probar la validez de los modelos matemáticos comparando las predicciones basadas en ellos con el resultado real de los experimentos. El ejemplo 6 es inusual porque podemos calcular el valor exacto de la cuenta en cualquier momento específico y compararlo con el valor aproximado pronosticado por (9.4.1.15) (consulte el Ejercicio 21). La siguiente tabla ofrece una comparación para un período de diez años. Cada respuesta exacta corresponde al momento del depósito de fin de año, y se supone que cada año tiene exactamente 52 semanas.


