| Ecuaciones diferenciales | 9.2. Ecuaciones diferenciales de primer orden |
9.2.4 Transformación de ecuaciones no lineales en ecuaciones separables
En la sección 9.2.1 encontramos que las soluciones de una ecuación lineal no homogénea
y′ + p(x)y = f (x)
son de la forma y = uy₁, donde y₁ es una solución no trivial de la ecuación complementaria
y′ + p(x)y = 0 (9.2.4.1)
y u es una solución de
u′y₁(x) = f (x).
Tenga en cuenta que esta última ecuación es separable, ya que se puede reescribir como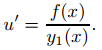
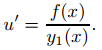
En esta sección, consideraremos ecuaciones diferenciales no lineales que no son separables para empezar, pero que pueden resolverse de una manera similar escribiendo sus soluciones en la forma y = uy₁, donde y₁ es una función conocida elegida adecuadamente y u satisface una ecuación separable. En este caso, diremos que transformamos la ecuación dada en una ecuación separable.
Ecuación de Bernoulli
Una ecuación de Bernoulli es una ecuación de la forma
y′ + p(x)y = f (x)y ͬ , (9.2.4.2)
donde r puede ser cualquier número real distinto de 0 o 1. (Tenga en cuenta que (9.2.4.2) es lineal si y solo si r = 0 o r = 1.) Podemos transformar (9.2.4.2) en una ecuación separable por variación de parámetros: si y₁ es una solución no trivial de (9.2.4.1), al sustituir y = uy₁ en (9.2.4.2) se obtiene
que es equivalente a la ecuación separable
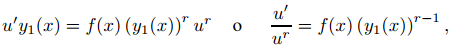
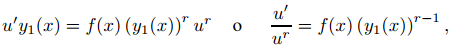
ya que y₁′ + p(x)y₁ = 0.
Ejemplo ilustrativo 9.2.4_1
Resuelve la ecuación de Bernoulli
y′ − y = xy². (9.2.4.3)
Solución:
Dado que y₁ = eˣ es una solución de y′ − y = 0, buscamos soluciones de (9.2.4.3) en la forma y = ueˣ, donde
u′eˣ = xu²e²ˣ o, de manera equivalente, u′ = xu²eˣ.
Separando variables, se obtiene
e integrando, se obtiene
Por lo tanto,
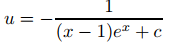
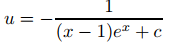
y
La figura 9.2.4.1 muestra el campo direccional y algunas curvas integrales de (9.2.4.3). ♦
Figura 9.2.4.1 Un campo de direcciones y curvas integrales para y′ − y = xy²
Otras ecuaciones no lineales que se pueden transformar en ecuaciones separables
Hemos visto que la ecuación de Bernoulli no lineal se puede transformar en una ecuación separable mediante la sustitución y = uy₁ si y₁ se elige adecuadamente. Ahora descubramos una condición suficiente para una ecuación diferencial de primer orden no lineal
y′ = f (x, y) (9.2.4.4)
de manera que se transforme en una ecuación separable equivalente de la misma manera. Al sustituir y = uy₁ en (9.2.4.4) se obtiene
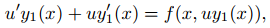
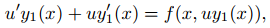
que es equivalente a
Si
para alguna función q, entonces (9.2.4.5) se convierte en
que es separable. Después de verificar soluciones constantes u ≡ u0 tales que q(u0) = u0, podemos separar las variables para obtener
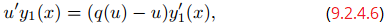
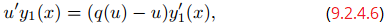
Ecuaciones no lineales homogéneas
En el texto, consideraremos solo la clase de ecuaciones más ampliamente estudiada para la que funciona el método del párrafo anterior. En los ejercicios 44 a 51 aparecen otros tipos de ecuaciones.
Se dice que la ecuación diferencial (9.2.4.4) es homogénea si x e y ocurren en f de tal manera que f (x, y) depende sólo de la relación y/x; es decir, (9.2.4.4) se puede escribir como
y′ = q(y/x) (9.2.4.7)
donde q = q(u) es una función de una sola variable. Por ejemplo,
y
son de la forma (9.2.4.7), con
q(u) = u + e−u y q(u) = u2 + u − 1,
respectivamente. El método general discutido anteriormente se puede aplicar a (9.2.4.7) con y1 = x (y por lo tanto y′1 = 1). Por tanto, sustituyendo y = ux en (9.2.4.7) se obtiene
u′x + u = q(u),
y separación de variables (después de verificar soluciones constantes u ≡ u0 tales que q(u0) = u0) produce
Antes de pasar a los ejemplos, señalamos algo que quizás ya haya notado: la definición de ecuación homogénea que se da aquí no es la misma que la definición dada en la Sección 9.2.1, donde dijimos que una ecuación lineal de la forma
y′ + p(x)y = 0
es homogénea. No nos disculpamos por esta inconsistencia, ya que no la creamos históricamente, se ha utilizado homogéneo en estas dos formas inconsistentes. El que tiene que ver con ecuaciones lineales es el más importante. Esta es la única sección del libro donde se aplicará el significado definido aquí.
Dado que y/x en general no está definido si x = 0, consideraremos soluciones de ecuaciones no homogéneas solo en intervalos abiertos que no contienen el punto x = 0.
Ejemplo ilustrativo 9.2.4_2
Resolver
Solución:
Sustituyendo y = ux en (9.2.4.8) se obtiene
Simplificando y separando variables, se obtiene
Integrando, se obtiene eu = ln|x| + c. Por lo tanto u = ln(ln|x| + c) y y = ux = xln(ln|x| + c).
La figura 9.2.4.2 muestra un campo de direcciones y curvas integrales para (9.2.4.8). ♦
Figura 9.2.4.2 Un campo direccional y algunas curvas integrales para y′ = (y + xe− y/x)/x
Ejemplo ilustrativo 9.2.4_3
(a) Resolver
x2y′ = y2 + xy − x2. (9.2.4.9)
(b) Resuelve el problema del valor inicial
x2y′ = y2 + xy − x2, y(1) = 2 (9.2.4.10)
Solución:
(a) Primero encontramos soluciones de (9.2.4.9) en intervalos abiertos que no contienen x = 0. Podemos reescribir (9.2.4.9) como
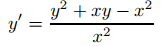
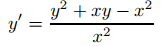
para x en cualquier intervalo de este tipo. Sustituyendo y = ux, se obtiene
entonces
u′x = u2 − 1. (9.2.4.11)
Por inspección, esta ecuación tiene las soluciones constantes u ≡ 1 y u ≡ −1. Por lo tanto, y = x y y = −x son soluciones de (9.2.4.9). Si u es una solución de (9.2.4.11) que no asume los valores ± 1 en algún intervalo, al separar las variables se obtiene
o, después de una expansión en fracciones parciales,
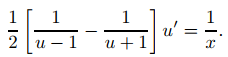
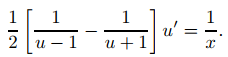
Multiplicar por 2 e integrar para obtener
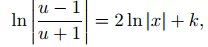
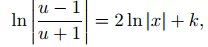
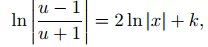
entonces
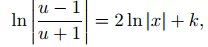
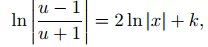
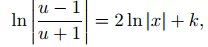
que se sostiene si
donde c es una constante arbitraria. Resolviendo para u, obtenemos
Por lo tanto
(9.2.4.13)
es una solución de (9.2.4.10) para cualquier elección de la constante c. Establecer c = 0 en (9.2.4.13) produce la solución y = x. Sin embargo, la solución y = −x no se puede obtener de (9.2.4.13). Por tanto, las soluciones de (9.2.4.9) en intervalos que no contienen x = 0 son y = −x y funciones de la forma (9.2.4.13).
La situación es más complicada si x = 0 está el intervalo abierto. Primero, observe que y = −x satisface (9.2.4.9) en (−∞, ∞). Si c1 y c2 son constantes arbitrarias, la función
(9.2.4.14)
es una solución de (9.2.4.9) en (a, b), donde
Te dejamos verificar esto. Para hacerlo, tenga en cuenta que si y es cualquier función de la forma (9.2.4.13), entonces y(0) = 0 y y′(0) = 1.
La figura 9.2.4.3 muestra un campo direccional y algunas curvas integrales para (9.2.4.9).
(b) Podríamos obtener c imponiendo la condición inicial y(1) = 2 en (9.2.4.13), y luego despejando c. Sin embargo, es más fácil de usar (9.2.4.12). Como u = y / x, la condición inicial y(1) = 2 implica que u(1) = 2. Sustituyendo esto en (9.2.4.12) se obtiene c = 1/3. Por tanto, la solución de (9.2.4.10) es
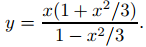
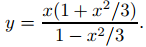
El intervalo de validez de esta solución es (−√3, √3). Sin embargo, el intervalo más grande en el que (9.2.4.10) tiene una solución única es (0, √3). Para ver esto, tenga en cuenta de (9.2.4.14) que cualquier función de la forma
(9.2.4.15)
es una solución de (9.2.4.10) en (a, √3), donde a = −1 / √c si c > 0 o a = −∞ si c ≤ 0. (¿Por qué esto no contradice el Teorema 9.2.3.1?)
La figura 9.2.4.4 muestra varias soluciones del problema del valor inicial (9.2.4.10). Tenga en cuenta que estas soluciones coinciden en (0, √3). ♦
|
Figura 9.2.4.3 Un campo de direcciones y curvas integrales para x2y′ = y2 + xy − x2 |
Figura 9.2.4.4 Soluciones del PVI x2y′ = y2 + xy − x2, y(1) = 2 |
En los dos últimos ejemplos pudimos resolver explícitamente las ecuaciones dadas. Sin embargo, esto no siempre es posible, como verá en los ejercicios.