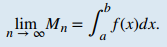(5. LA INTEGRAL Y TÉCNICAS DE INTEGRACIÓN)
Ejercicios propuestos para el Capítulo 5.13
Integración numérica: Objetivos de aprendizaje
5.13.1. Aproxima el valor de una integral definida usando la regla del punto medio y la regla del trapecio.
5.13.2. Determine el error absoluto y relativo al usar una técnica de integración numérica.
5.13.3. Estime el error absoluto y relativo usando una fórmula ligada a error.
5.13.4. Reconozca cuándo las reglas del punto medio y la del trapecio sobreestiman o subestiman el verdadero valor de una integral.
5.13.5. Use la regla de Simpson para aproximar el valor de una integral definida a una precisión dada.
Las antiderivadas de muchas funciones no se pueden expresar o no se pueden expresar fácilmente en forma cerrada (es decir, en términos de funciones conocidas). En consecuencia, en lugar de evaluar directamente integrales definidas de estas funciones, recurrimos a varias técnicas de integración numérica para aproximar sus valores. En esta sección exploramos varias de estas técnicas. Además, examinamos el proceso de estimar el error al usar estas técnicas.
La regla del punto medio
Anteriormente en este texto definimos la integral definida de una función sobre un intervalo como el límite de las sumas de Riemann. En general, cualquier suma de Riemann de una función f (x) en un intervalo [a, b] puede verse como una estimación de
Recuerde que una suma de Riemann de una función f (x) en un intervalo [a, b] se obtiene seleccionando una partición
P = {x₀, x₁, x₂,…, xn}, donde a = x₀ < x₁ < x₂ < ⋯ < xn = b
y un conjunto
donde 
para todo i.
La suma de Riemann correspondiente a la partición P y el conjunto S está dada por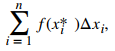
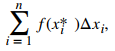
dónde
es la longitud del i-ésimo subintervalo.
TEOREMA 5.13_1. La regla del punto medio
|
Suponga que f (x) es continua en [a, b]. Sea n un número entero positivo y Δx = (b − a)/n. Si [a, b] se divide en n subintervalos, cada uno de longitud Δx, y mᵢ es el punto medio del i-ésimo subintervalo, establezca entonces |
Como podemos ver en la figura 5.13_1, si f (x) ≥ 0 sobre [a, b], entonces
corresponde a la suma de las áreas de rectángulos que se aproximan al área entre la gráfica de f (x) y el eje x sobre [a, b]. La gráfica muestra los rectángulos correspondientes a M₄ para una función no negativa en un intervalo cerrado [a, b].
EJEMPLO ILUSTRATIVO 5.13_1. Usar la regla del punto medio con M₄
Utilice la regla del punto medio para estimar
utilizando cuatro subintervalos. Compare el resultado con el valor real de esta integral.
Solución:
Cada subintervalo tiene una longitud Δx = (1− 0)/4 = 1/4. Por tanto, los subintervalos constan de
Los puntos medios de estos subintervalos son {1/8, 3/8, 5/8, 7/8}. Así,
Ya que
vemos que la regla del punto medio produce una estimación que es algo cercana al valor real de la integral definida.
EJEMPLO ILUSTRATIVO 5.13_2. Usar la regla del punto medio con M₆
Utilice M₆ para estimar la longitud de la curva y = (1/2)x² en [1, 4].
Solución:
La longitud de y = (1/2)x² en [1, 4] es
Dado que dy/dx = x, esta integral se convierte en
Si [1, 4] se divide en seis subintervalos, entonces cada subintervalo tiene una longitud Δx = (4 −1)/6 = 1/2 y los puntos medios de los subintervalos son {5/4, 7/4, 9/4, 11/4, 13/4, 15/4}. Si establecemos f (x) = √(1 + x²),
Ejercicio de control 5.13_1
Utilice la regla del punto medio con n = 2 para estimar
