| 5. La integral y Técnicas de integración | Ejercicios propuestos del Capítulo 5.10 |
5.10 Sustitución trigonométrica
Objetivos de aprendizaje:
5.10.1 Resuelva problemas de integración que involucran la raíz cuadrada de una suma o diferencia de dos cuadrados.
En esta sección, exploramos integrales que contienen expresiones de la forma √(a² − x²), √(a² + x²) y √(x² − a²), donde los valores de a son positivos. Ya hemos encontrado y evaluado integrales que contienen algunas expresiones de este tipo, pero muchas aún permanecen inaccesibles. La técnica de sustitución trigonométrica resulta muy útil al evaluar estas integrales. Esta técnica utiliza la sustitución para reescribir estas integrales como integrales trigonométricas.
Integrales que involucran √(a² − x²)
Antes de desarrollar una estrategia general para integrales que contengan √(a² − x²), considere la integral ∫√(9 − x²)dx. Esta integral no puede evaluarse utilizando ninguna de las técnicas que hemos discutido hasta ahora. Sin embargo, si hacemos la sustitución x = 3senθ, tenemos dx = 3cosθdθ. Después de sustituir en la integral, tenemos

Después de simplificar, tenemos

Dejando 1 − sen²θ = cos²θ, ahora tenemos

Suponiendo que cosθ ≥ 0, tenemos

En este punto, podemos evaluar la integral utilizando las técnicas desarrolladas para integrar potencias y productos de funciones trigonométricas. Antes de completar este ejemplo, echemos un vistazo a la teoría general detrás de esta idea.
Para evaluar integrales que involucran √(a² − x²), hacemos la sustitución x = asenθ y dx = acosθ. Para ver que esto realmente tiene sentido, considere el siguiente argumento: El dominio de √(a² − x²) es [−a, a]. Por lo tanto, −a ≤ x ≤ a. En consecuencia, −1 ≤ x/a ≤ 1. Como el rango de senx sobre [-(π/2), π/2] es [−1, 1], existe un ángulo único θ que satisface -π/2 ≤ θ ≤ π/2, de modo que senθ = x/a, o equivalente, de modo que x = asenθ. Si sustituimos x = asenθ en √(a² − x²), obtenemos
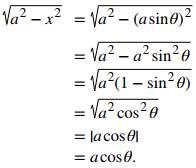
Como cosθ ≥ 0 en −π/2 ≤ θ ≤ π/2 y a > 0, |acosθ| = acosθ. Podemos ver, a partir de esta discusión, que al hacer la sustitución x = asenθ, podemos convertir una integral que involucra un radical en una integral que involucra funciones trigonométricas. Después de evaluar la integral, podemos convertir la solución nuevamente en una expresión que implique x. Para ver cómo hacer esto, comencemos asumiendo que 0 < x < a. En este caso, 0 < θ < π/2. Como senθ = x/a, podemos dibujar el triángulo de referencia en la Figura 5.10_1 para ayudar a expresar los valores de cosθ, tanθ y las funciones trigonométricas restantes en términos de x. Se puede demostrar que este triángulo en realidad produce los valores correctos de las funciones trigonométricas evaluadas en θ para todos los θ que satisfacen −π/2 ≤ θ ≤ π/2. Es útil observar que la expresión √(a² − x²) en realidad aparece como la longitud de un lado del triángulo. Por último, si θ aparece por sí mismo, usamos θ = sen⁻¹(x/a).

Figura 5.10_1 Un triángulo de referencia puede ayudar a expresar las funciones trigonométricas evaluadas en θ en términos de x.
La parte esencial de esta discusión se resume en la siguiente estrategia de resolución de problemas.
ESTRATEGIA PARA RESOLVER PROBLEMAS 5.10_1: INTEGRAR EXPRESIONES QUE INCLUYEN √(a² − x²)
- Es una buena idea asegurarse de que la integral no pueda evaluarse fácilmente de otra manera. Por ejemplo, aunque este método se puede aplicar a integrales de la forma
 cada uno puede integrarse directamente por fórmula o por una simple sustitución en u.
cada uno puede integrarse directamente por fórmula o por una simple sustitución en u. - Realice la sustitución x = asenθ y dx = acosθdθ. Nota: Esta sustitución produce √(a² − x²) = acosθ.
- Simplifica la expresión.
- Evalúe la integral utilizando técnicas de la sección sobre integrales trigonométricas.
- Use el triángulo de referencia de la Figura 5.10_1 para reescribir el resultado en términos de x. También es posible que necesite usar algunas identidades trigonométricas y la relación θ = sen⁻¹(x/a). ♦
El siguiente ejemplo demuestra la aplicación de esta estrategia de resolución de problemas.
EJEMPLO ILUSTRATIVO 5.10_1. Integrando una expresión que involucra√(a² − x²)
Evalúe ∫√(9 − x²)dx.
Solución:
Comience haciendo las sustituciones x = 3senθ y dx = 3cosθdθ. Como senθ = x/3, podemos construir el triángulo de referencia que se muestra en la siguiente figura.

De tal modo que

♦
EJEMPLO ILUSTRATIVO 5.10_2. Integrando una expresión que involucra √(a² − x²)
Evaluar
Solución:
Primero haga las sustituciones x = 2senθ y dx = 2cosθdθ. Como senθ = x/2, podemos construir el triángulo de referencia que se muestra en la siguiente figura.
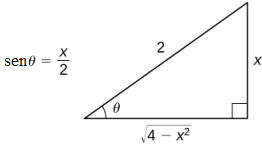
De tal manera que
 ♦
♦
En el siguiente ejemplo, vemos que a veces tenemos una opción de métodos.
EJEMPLO ILUSTRATIVO 5.10_3. Integrando una expresión que involucra √(a² − x²). Dos maneras distintas
Evalúe ∫x³(1 − x²)dx de dos maneras: primero usando la sustitución u = 1 − x² y luego usando una sustitución trigonométrica.
Solución:
Método 1
Sea u = 1 − x² y, por lo tanto, x² = 1 − u. Entonces, du = −2xdx. En este caso, la integral se convierte en
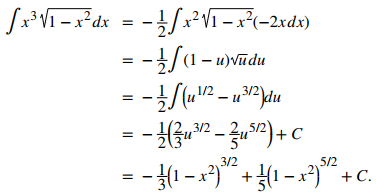
Método 2
Deje x = senθ. En este caso, dx = cosθdθ. Usando esta sustitución, tenemos
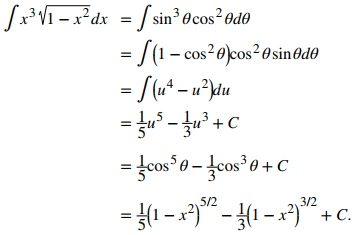
No importa el método usado, si las operaciones son correctas, se obtiene la misma solución. ♦
Ejercicio de control 5.10.1
Reescriba la integral $\int \frac{x^3}{\sqrt{25 – x^2}} \, dx$ usando la sustitución trigonométrica apropiada (no evalúe la integral). ♦
Integrando expresiones que involucran √(a² + x²)
Para las integrales que contienen √(a² + x²), consideremos primero el dominio de esta expresión. Como √(a² + x²) se define para todos los valores reales de x, restringimos nuestra elección a aquellas funciones trigonométricas que tienen un rango de todos los números reales. Por lo tanto, nuestra elección se limita a seleccionar x = atanθ o x = acotθ. Cualquiera de estas sustituciones realmente funciona, pero la sustitución estándar es x = atanθ o, de manera equivalente, tanθ = x/a. Con esta sustitución, suponemos que -π/2) < θ < π/2, de modo que también tenemos θ = tan⁻¹(x/a). El procedimiento para usar esta sustitución se describe en la siguiente estrategia de resolución de problemas.
ESTRATEGIA PARA RESOLVER PROBLEMAS 5.10_2: INTEGRAR EXPRESIONES QUE INCLUYEN √(a² + x²)
- Verifique si la integral se puede evaluar fácilmente utilizando otro método. En algunos casos, es más conveniente usar un método alternativo.
- Sustituya x = atanθ y dx = asec²θdθ. Esta sustitución produce
 (Dado que −π/2 < θ < π/2 y secθ > 0 durante este intervalo, |asecθ| = asecθ.)
(Dado que −π/2 < θ < π/2 y secθ > 0 durante este intervalo, |asecθ| = asecθ.) - Simplifica la expresión.
- Evalúe la integral utilizando técnicas de la sección sobre integrales trigonométricas.
- Use el triángulo de referencia de la Figura 5.10_4 para reescribir el resultado en términos de x. También es posible que necesite usar algunas identidades trigonométricas y la relación θ = tan⁻¹(x/a). (Nota: el triángulo de referencia se basa en el supuesto de que x > 0; sin embargo, las relaciones trigonométricas producidas a partir del triángulo de referencia son las mismas que las relaciones para las cuales x ≤ 0.) ♦
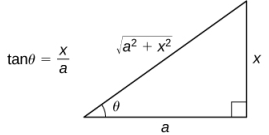
Figura 5.10_4 Se puede construir un triángulo de referencia para expresar las funciones trigonométricas evaluadas en θ en términos de x.
EJEMPLO ILUSTRATIVO 5.10_4. Integrando una expresión que involucra √(a² + x²)
Evaluar y verifique la solución diferenciando.
y verifique la solución diferenciando.
Solución:
Comience con la sustitución x = tanθ y dx = sec²θdθ. Como tanθ = x, dibuja el triángulo de referencia en la siguiente figura.

De tal modo que
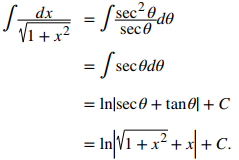
Para verificar la solución, diferencie:
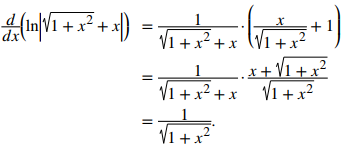
Como √(1 + x²) + x > 0 para todos los valores de x, podríamos reescribir ln∣√(1 + x²) + x∣ + C = ln (√(1 + x²) + x) + C, si lo desea. ♦
EJEMPLO ILUSTRATIVO 5.10_5. Integrando una expresión que involucra √(a² + x²)
Evaluar Usando una sustitución diferente a la del ejemplo anterior.
Usando una sustitución diferente a la del ejemplo anterior.
Solución:
Use la sustitución x = senhθ.
Debido a que senhθ tiene un rango de todos los números reales, y 1 + senh²θ = cosh²θ, también podemos usar la sustitución x = senhθ para evaluar esta integral. En este caso, dx = coshθdθ. Por consiguiente,
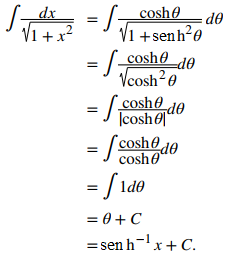
Análisis
Esta respuesta se ve bastante diferente de la respuesta obtenida usando la sustitución x = tanθ. Para ver que las soluciones son las mismas, establezca y = senh⁻¹x. Por lo tanto, senhy = x. De esta ecuación obtenemos:
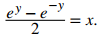
Después de multiplicar ambos lados por 2eʸ y reescribir, esta ecuación se convierte en:
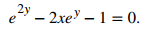
Usa la ecuación cuadrática para resolver por eʸ:
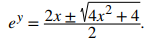
Simplificando, tenemos:

Como x − √(x² + 1) < 0, debe ser el caso de que eʸ = x + √(x² + 1). Así,

Por último, obtenemos
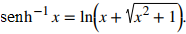
Después de hacer la observación final que x + √(x² + 1) > 0,
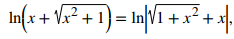
vemos que los dos métodos diferentes produjeron soluciones equivalentes. ♦
EJEMPLO ILUSTRATIVO 5.10_6. Encontrar una longitud de arco
Encuentre la longitud de la curva y = x² sobre el intervalo [0, 1/2].
Solución:
Como dy/dx = 2x, la longitud del arco viene dada por
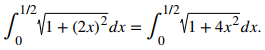
Para evaluar esta integral, use la sustitución x = (1/2)tanθ y dx = (1/2)sec²θdθ. También necesitamos cambiar los límites de la integración. Si x = 0, entonces θ = 0 y si x = 1/2, entonces θ = π/4. Así,

♦
Ejercicio de control 5.10.2
Reescriba $\int x^3 \sqrt{x^2 + 4} \, dx$ mediante una sustitución que involucre a $\tan \theta$. ♦
Integrando expresiones que involucran √(x² − a²)
El dominio de la expresión √(x² − a²) es (−∞, −a] ∪ [a, + ∞). Por lo tanto, x ≤ − a o x ≥ a. Por lo tanto, x/a ≤ − 1 o x/a ≥ 1. Dado que estos intervalos corresponden al rango de secθ en el conjunto [0, π/2) ∪ (π/2, π], tiene sentido usar la sustitución secθ = x/a o, de manera equivalente, x = asecθ, donde 0 ≤ θ < π/2 o π/2 < θ ≤ π. La sustitución correspondiente para dx es dx = asecθtanθdθ. El procedimiento para utilizar esta sustitución se describe en la siguiente estrategia de resolución de problemas.
ESTRATEGIA DE RESOLUCIÓN DE PROBLEMAS 5.10_3: INTEGRALES QUE INVOLUCRAN √(x² − a²)
1. Verifique si la integral no puede evaluarse utilizando otro método. Si es así, podríamos considerar aplicar una técnica alternativa.
2. Sustituya x = asecθ y dx = asecθtanθdθ. Esta sustitución produce

Para x ≥ a, |atanθ| = atanθ y para x ≤ − a, |atanθ| = −atanθ.
3. Simplifica la expresión.
4. Evalúe la integral utilizando técnicas de la sección sobre integrales trigonométricas.
5. Use los triángulos de referencia de la figura 5.10_6 para reescribir el resultado en términos de x. También es posible que necesite usar algunas identidades trigonométricas y la relación θ = sec ⁻¹(x/a). (Nota: Necesitamos ambos triángulos de referencia, ya que los valores de algunas de las relaciones trigonométricas son diferentes dependiendo de si x ≥ a o x ≤ − a.) ♦
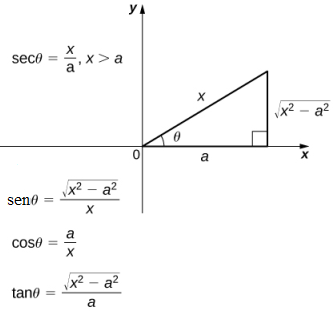

Figura 5.10_6 Use el triángulo de referencia apropiado para expresar las funciones trigonométricas evaluadas en θ en términos de x.
EJEMPLO ILUSTRATIVO 5.10_7. Encontrar el área de una región
Encuentre el área de la región entre la gráfica de f (x) = √(x² − 9) y el eje x sobre el intervalo [3, 5].
Solución:
Primero, dibuje un gráfico aproximado de la región descrita en el problema, como se muestra en la siguiente figura.
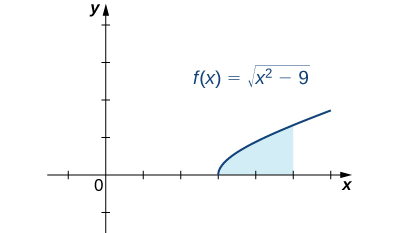
Figura 5.10_7 Calcular el área de la región sombreada requiere evaluar una integral con una sustitución trigonométrica.
Podemos ver que el área está dada por

Para evaluar esta integral definida, sustituya x = 3secθ y dx = 3secθtanθdθ. También debemos cambiar los límites de la integración. Si x = 3, entonces 3 = 3secθ y por lo tanto θ = 0. Si x = 5, entonces θ = sec⁻¹(5/3). Después de hacer estas sustituciones y simplificar, tenemos
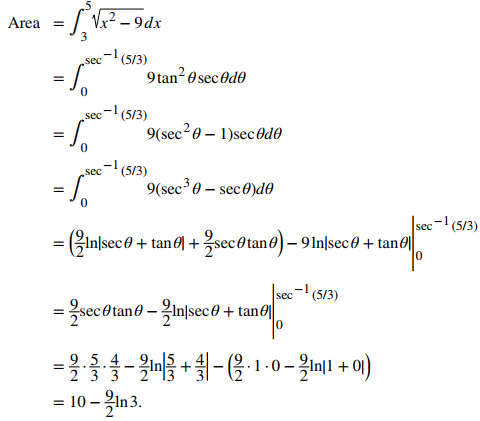
♦
Ejercicio de control 5.10.3
Evalúe $\int \frac{dx}{\sqrt{x^2 \, – \, 4}}$. Asuma que $x > 2$. ♦

 cada uno puede integrarse directamente por fórmula o por una simple sustitución en u.
cada uno puede integrarse directamente por fórmula o por una simple sustitución en u.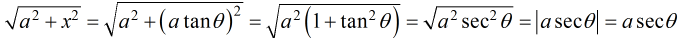 (Dado que −π/2 < θ < π/2 y secθ > 0 durante este intervalo, |asecθ| = asecθ.)
(Dado que −π/2 < θ < π/2 y secθ > 0 durante este intervalo, |asecθ| = asecθ.)