CONTINUIDAD: Objetivos de aprendizaje
2.4.1 Explique las tres condiciones para la continuidad en un punto.
2.4.2 Describe tres tipos de discontinuidades.
2.4.3 Definir continuidad en un intervalo.
2.4.4 Establezca el teorema de los límites de las funciones compuestas.
2.4.5 Proporcione un ejemplo del teorema del valor intermedio.
Muchas funciones tienen la propiedad de que sus gráficas pueden trazarse con un lápiz sobre una hoja de papel sin levantar el lápiz de la hoja. Tales funciones se llaman continuas. Otras funciones tienen puntos en los que se produce una ruptura en el gráfico, pero satisfacen esta propiedad de continuidad en intervalos contenidos en sus dominios. Son continuos en estos intervalos y se dice que tienen una discontinuidad en un punto donde ocurre una ruptura.
Comenzamos nuestra investigación de continuidad explorando lo que significa que una función tenga continuidad en un punto. Intuitivamente, una función es continua en un punto particular si no hay ruptura en su gráfico en ese punto.
Continuidad en un punto
Antes de ver una definición formal de lo que significa que una función sea continua en un punto, consideremos varias funciones que no cumplen con nuestra noción intuitiva de lo que significa ser continuo en un punto. Luego creamos una lista de condiciones que evitan tales fallas.
Nuestra primera función de interés se muestra en la figura 2.4_1. Vemos que la gráfica de f (x) tiene un agujero en a. De hecho, el valor f (a) no está definida. Como mínimo, para que f (x) sea continua en a, necesitamos la siguiente condición:
i. f (a) esté definido.

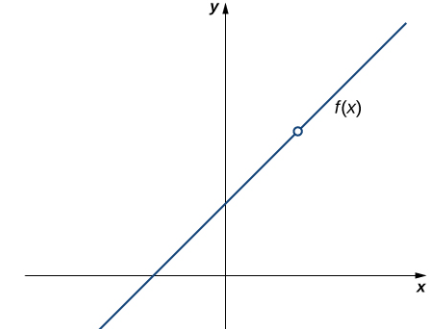
Sin embargo, como vemos en la Figura 2.4_2, esta condición por sí sola es insuficiente para garantizar la continuidad en el punto a. Aunque el valor f (a) está definido, la función tiene una brecha en a. En este ejemplo, la brecha existe porque limx → a f (x) no existe. Debemos agregar otra condición para la continuidad en a, a saber,
ii. limx → a f (x) exista.


Sin embargo, como vemos en la Figura 2.4_3, estas dos condiciones por sí mismas no garantizan la continuidad en un punto. La función en esta figura satisface nuestras dos primeras condiciones, pero aún no es continua en a. Debemos agregar una tercera condición a nuestra lista:
iii. limx → a f (x) = f (a).


Ahora ponemos nuestra lista de condiciones juntas y formamos una definición de continuidad en un punto.
DEFINICIÓN 2.4.1. Continuidad de una función en un punto
|
Una función f (x) es continua en un punto a si y solo si se cumplen las siguientes tres condiciones:
Una función es discontinua en un punto a si no puede ser continua en a. |
El siguiente procedimiento se puede utilizar para analizar la continuidad de una función en un punto utilizando la definición anterior.
ESTRATEGIA PARA RESOLVER PROBLEMAS: DETERMINAR LA CONTINUIDAD EN UN PUNTO
|
1. Verifique si f (a) está definido. Si f (a) no está definido, no necesitamos ir más allá. La función no es continua en a. Si se define f (a), continúe con el paso 2. 2. Calcule limx → a f (x). En algunos casos, es posible que tengamos que hacer esto calculando primero limx → a− f (x) y limx → a+ f (x). Si limx → a f (x) no existe (es decir, no es un número real), entonces la función no es continua en a y el problema está resuelto. Si existe limx → a f (x), continúe con el paso 3. 3. Compare f (a) y limx → a f (x). Si limx → a f (x) ≠ f (a), entonces la función no es continua en a. Si limx → a f (x) = f (a), entonces la función es continua en a. |
Los siguientes tres ejemplos ilustran cómo aplicar esta definición para determinar si una función es continua en un punto dado. Estos ejemplos muestran situaciones en las que cada una de las condiciones para la continuidad en la definición tiene éxito o falla.
EJEMPLO 2.4_1. Determinación de la continuidad en un punto, condición 1
Usando la definición 2.4.1, determine si la función f (x) = (x² − 4) / (x − 2) es continua en x = 2. Justifica la conclusión.
Solución:
Comencemos tratando de calcular f (2). Podemos ver que f (2) = 0/0, que no está definido. Por lo tanto, f (x) = (x² − 4) / (x − 2) es discontinuo en 2 porque f (2) no está definido. La gráfica de f (x) se muestra en la figura 2.4_4.

EJEMPLO 2.4_2. Determinación de la continuidad en un punto, condición 2
Usando la definición 2.4_1, determine si la función


es continuo en x = 3. Justifica la conclusión.
Solución:
Comencemos tratando de calcular f (3).


Por lo tanto, f (3) está definida. A continuación, calculamos limx → 3 f (x). Para hacer esto, debemos calcular limx → 3− f (x) y limx → 3+ f (x):


y


Por lo tanto, limx → 3 f (x) no existe. Por lo tanto, f (x) no es continua en 3. La gráfica de f (x) se muestra en la Figura 2.4_5.


EJEMPLO 2.4_3. Determinación de la continuidad en un punto, condición 3
Usando la definición, determine si la función


Es continua en x = 0.
Solución:
Primero, observe que
f (0) = 1.
Ahora,


Por último, compare f (0) y limx → 1 f (x). Observamos que


Como se cumplen las tres condiciones en la definición 2.4.1 de continuidad, f (x) es continua en x = 0.
Al aplicar la definición de continuidad y los teoremas previamente establecidos sobre la evaluación de límites, podemos establecer el siguiente teorema.
TEOREMA 2.4.1 Continuidad de polinomios y funciones racionales
| Los polinomios y las funciones racionales son continuas en cada punto de sus dominios. |
PruebaAnteriormente, mostramos que si p(x) y q(x) son polinomios, limx → a p x) = p(a) para cada polinomio p(x) y
siempre que q(a) ≠ 0. Por lo tanto, los polinomios y las funciones racionales son continuas en sus dominios. |
EJEMPLO 2.4_4. Continuidad de una función racional
¿Para qué valores de x es f (x) = (x + 1)/(x − 5) continua?
Solución:
La función racional f (x) = (x + 1)/(x − 5) es continua para cada valor de x excepto x = 5.
Tipos de discontinuidades
Como hemos visto en el ejemplo 2.4_ y el ejemplo 2.4_2, las discontinuidades adquieren varias apariencias diferentes. Clasificamos los tipos de discontinuidades que hemos visto hasta ahora como discontinuidades removibles, discontinuidades infinitas o discontinuidades de salto. Intuitivamente, una discontinuidad removible es una discontinuidad para la cual hay un agujero en el gráfico, una discontinuidad de salto es una discontinuidad no infinita para la cual las secciones de la función no se encuentran, y una discontinuidad infinita es una discontinuidad ubicada en una asíntota vertical. La figura 2.4_6 ilustra las diferencias en estos tipos de discontinuidades. Aunque estos términos proporcionan una forma práctica de describir tres tipos comunes de discontinuidades, tenga en cuenta que no todas las discontinuidades encajan perfectamente en estas categorías.






Figura 2.4_6 Las discontinuidades se clasifican en (a) removibles, (b) saltos o (c) infinitas.
Estas tres discontinuidades se definen formalmente de la siguiente manera:
DEFINICIÓN 2.4.2. Tres tipos de discontinuidad
|
Si f (x) es discontinua en a, entonces 1. f tiene una discontinuidad removible en a si existe limx → a f (x). (Nota: cuando afirmamos que limx → a f (x) existe, queremos decir que limx → a f (x) = L, donde L es un número real). 2. f tiene una discontinuidad de salto en a si limx → a− f (x) y limx → a+ f (x) existen, pero limx → a− f (x) ≠ limx → a+ f (x). (Nota: cuando afirmamos que limx → a− f (x) y limx → a+ f (x) existen, queremos decir que ambos tienen un valor real y que ninguno toma los valores ± ∞.) 3. f tiene una discontinuidad infinita en a si limx → a− f (x) = ± ∞ o limx → a+ f (x) = ± ∞. |
EJEMPLO 2.4_5. Clasificación de una discontinuidad
En el ejemplo 2.4_1, mostramos que


es discontinuo en x = 2. Clasifique esta discontinuidad como removible, salto o infinita.
Solución:
Para clasificar la discontinuidad en 2 debemos evaluar limx → 2 f (x):


Dado que f es discontinuo en 2 y limx → 2 f (x) existe, f tiene una discontinuidad removible en x = 2.
EJEMPLO 2.4_6. Clasificación de una discontinuidad
En el ejemplo 2.4_2, mostramos que


es discontinuo en x = 3. Clasifique esta discontinuidad como removible, salto o infinita.
Solución:
Anteriormente, mostramos que f es discontinua en 3 porque el limx → 3 f (x) no existe. Sin embargo, dado que limx → 3− f (x) = – 5 y limx → 3+ f (x) = 4 existen, concluimos que la función tiene una discontinuidad de salto en 3.
EJEMPLO 2.4_7. Clasificación de una discontinuidad
Determine si f (x) = (x + 2)/(x + 1) es continua en −1. Si la función es discontinua en −1, clasifique la discontinuidad como removible, salto o infinita.
Solución:
El valor de la función f (−1) no está definido. Por lo tanto, la función no es continua en −1. Para determinar el tipo de discontinuidad, debemos determinar el límite en −1. Vemos que
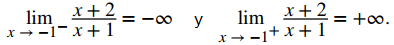
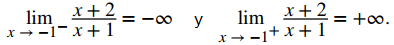
Por lo tanto, la función tiene una discontinuidad infinita en −1.
Ejercicios resueltos
Determine si la siguiente función es continua en el punto señalado. Si es discontinua en el punto, diga qué tipo de discontinuidad tiene?
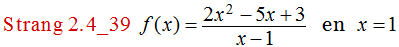
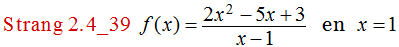
Determine si la siguiente función es continua en el punto señalado. Si es discontinua en el punto, diga qué tipo de discontinuidad tiene?


Determine si la siguiente función es continua en el punto señalado. Si es discontinua en el punto, diga qué tipo de discontinuidad tiene?


Determine si la siguiente función es continua en el punto señalado. Si es discontinua en el punto, diga qué tipo de discontinuidad tiene?




