Diferenciación implícita: Objetivos de aprendizaje
3.8.1. Encuentre la derivada de una función complicada (definida implícitamente) utilizando la diferenciación implícita.
3.8.2. Use la diferenciación implícita para determinar la ecuación de una recta tangente.
Ya hemos estudiado cómo encontrar ecuaciones de rectas tangentes a funciones y la tasa de cambio de una función en un punto específico. En todos estos casos teníamos la ecuación explícita para la función y las diferenciamos explícitamente. Supongamos, en cambio, que queremos determinar la ecuación de una recta tangente a una curva arbitraria o la tasa de cambio de una curva arbitraria en un punto. En esta sección, resolvemos estos problemas encontrando las derivadas de funciones que definen y implícitamente en términos de x.
Diferenciación implícita
En la mayoría de las discusiones de matemáticas, si la variable dependiente y es una función de la variable independiente x, expresamos y en términos de x. Si este es el caso, decimos que y es una función explícita de x. Por ejemplo, cuando escribimos la ecuación y = x² + 1, estamos definiendo y explícitamente en términos de x. Por otro lado, si la relación entre la función y y la variable x se expresa mediante una ecuación donde y no se despeja completamente en términos de x, decimos que la ecuación define y implícitamente en términos de x. Por ejemplo, la ecuación y − x² = 1 define la función y = x² + 1 implícitamente.
La diferenciación implícita nos permite encontrar pendientes de tangentes a curvas que claramente no son funciones (fallan en la prueba de la recta vertical). Estamos usando la idea de que porciones de y son funciones que satisfacen la ecuación dada, pero que y no es realmente una función de x.
En general, una ecuación define una función implícitamente si la función satisface esa ecuación. Una ecuación puede definir muchas funciones diferentes implícitamente. Por ejemplo, las funciones
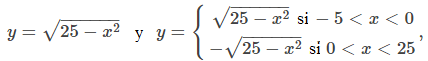
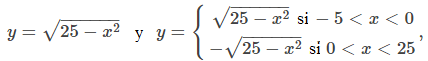
que se ilustran en la figura 3.8_1, son solo tres de las muchas funciones definidas implícitamente por la ecuación x² + y² = 25.

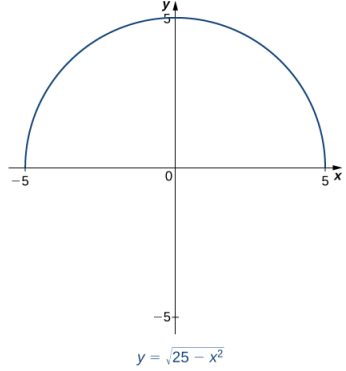

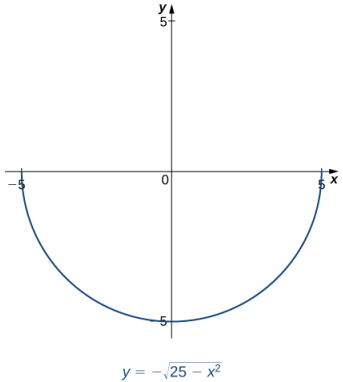



Figura 3.8_1 La ecuación x² + y² = 25 define muchas funciones implícitamente.
Si queremos encontrar la pendiente de la recta tangente a la gráfica de x² + y² = 25 en el punto (3, 4), podríamos evaluar la derivada de la función y = √(25 − x²) en x = 3. Por otro lado, si queremos la pendiente de la recta tangente en el punto (3, −4), podríamos usar la derivada de y = −√(25 − x²). Sin embargo, no siempre es fácil despejar una función definida implícitamente por una ecuación. Afortunadamente, la técnica de diferenciación implícita nos permite encontrar la derivada de una función definida implícitamente sin tener que resolverla explícitamente. El proceso de encontrar dy/dx usando diferenciación implícita se describe en la siguiente estrategia de resolución de problemas.
ESTRATEGIA DE RESOLUCIÓN DE PROBLEMAS: DIFERENCIACIÓN IMPLÍCITA
|
Para realizar una diferenciación implícita en una ecuación que define una función y implícitamente en términos de una variable independiente x, utilice los siguientes pasos:
|
Ejemplo ilustrativo 3.8_1. Usando la diferenciación implícita
Suponiendo que y se define implícitamente por la ecuación x² + y² = 25, encuentre dy/dx.
Solución:
Siga los pasos de la estrategia de resolución de problemas.
Paso 1. Diferenciar ambos lados de la ecuación:
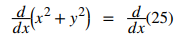
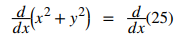
Paso 1.1. Usa la regla de la suma a la izquierda. A la derecha d/dx (25) = 0:
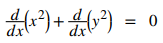
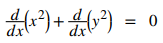
Paso 1.2 Toma las derivadas, entonces d/dx (x²) = 2x y d/dx (y²) = 2y⋅dy/dx:
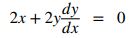
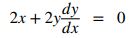
Paso 2. Mantenga los términos con dy/dx a la izquierda. Mueve los términos restantes a la derecha:
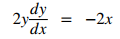
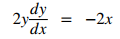
Paso 4. Divide ambos lados de la ecuación por 2y. (El paso 3 no se aplica en este caso):
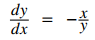
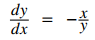
Análisis
Tenga en cuenta que la expresión resultante para dy/dx está dada tanto en términos de la variable independiente x como de la variable dependiente y. Aunque en algunos casos puede ser posible expresar dy/dx solo en términos de x, generalmente no es posible hacerlo. ◊
Ejemplo ilustrativo 3.8_2. Uso de la diferenciación implícita y la regla del producto
Suponiendo que y se define implícitamente por la ecuación x³seny + y = 4x + 3, encuentre dy/dx.
Solución:
Paso 1: diferenciar ambos lados de la ecuación:
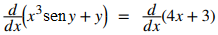
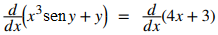
Paso 1.1: aplique la regla de suma a la izquierda. A la derecha, d/dx (4x + 3) = 4:
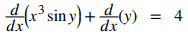
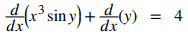
Paso 1.2: usa la regla del producto para encontrar d/dx (x³ seny). Observe que d/dx (y) = dy/dx:
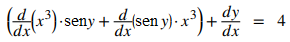
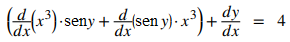
Paso 1.3: Sabemos que d/dx (x³) = 3x². Utilice la regla de cadena para obtener d/dx (seny) = cosy⋅dy/dx:
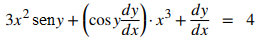
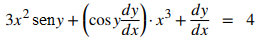
Paso 2: mantenga todos los términos que contengan dy/dx en el miembro
izquierdo. Mueva todos los demás términos a la derecha:


Paso 3: Factoriza dy/dx a la izquierda:


Paso 4: despeje dy/dx dividiendo ambos lados de la ecuación por x³ cosy + 1:


Ejemplo ilustrativo 3.8_3. Uso de la diferenciación implícita para encontrar una segunda derivada
Encuentre d²y/dx² si x² + y² = 25.
Solución:
En el ejemplo 3.8_1, mostramos que dy/dx = −xy. Podemos tomar la derivada de ambos lados de esta ecuación para encontrar d²y/dx²:


En este punto, hemos encontrado una expresión para d²y/dx². Podemos simplificar aún más la expresión recordando que x² + y² = 25 y haciendo esta sustitución en el numerador para obtener d²y/dx² = −25/y³. ◊
Encontrar rectas tangentes derivando implícitamente
Ahora que hemos visto la técnica de diferenciación implícita, podemos aplicarla al problema de encontrar ecuaciones de rectas tangentes a curvas descritas por ecuaciones.
Ejemplo ilustrativo 3.8_4. Encontrar una recta tangente a una circunferencia
Encuentre la ecuación de la recta tangente a la curva x² + y² = 25 en el punto (3, −4).
Solución:
Aunque podríamos encontrar esta ecuación sin usar la diferenciación implícita, usar ese método lo hace mucho más fácil. En el ejemplo 3.8_1, encontramos que dy/dx = −x/y.
La pendiente de la recta tangente se encuentra sustituyendo (3, −4) en esta expresión. En consecuencia, la pendiente de la recta tangente es


Usando el punto (3, −4) y la pendiente 3/4 en la ecuación punto-pendiente de la recta, obtenemos la ecuación y = (3/4)x − 25/4 (Figura 3.8_2).

Ejemplo ilustrativo 3.8_5. Encontrar la ecuación de la recta tangente a una curva
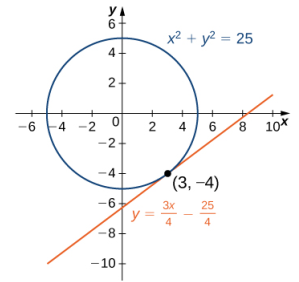
Encuentre la ecuación de la recta tangente a la gráfica de y³ + x³ − 3xy = 0 en el punto (3/2, 3/2) (Figura 3.8_3). Esta curva se conoce como folio (u hoja) de Descartes.
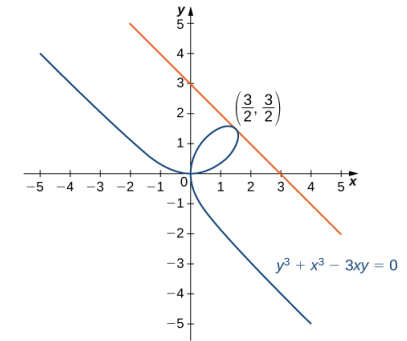
Solución:
Comience por encontrar dy/dx:


Ahora, sustituya (3/2, 3/2) en dy/dx = (3y − 3x²)/(3y² − 3x) para encontrar la pendiente de la recta tangente:


Finalmente, sustitúyase en la ecuación punto-pendiente de la recta para obtener:
y = −x + 3. ◊
Ejemplo ilustrativo 3.8_6. Aplicando la diferenciación implícita
En un videojuego simple, un cohete viaja en una órbita elíptica cuyo camino se describe mediante la ecuación 4x² + 25y² = 100. El cohete puede disparar misiles a lo largo de rectas tangentes a su camino. El objetivo del juego es destruir un asteroide entrante que viaja a lo largo del eje x positivo hacia (0, 0). Si el cohete dispara un misil cuando está ubicado en (3, 8/5), ¿dónde se intersecará con el eje x?
Solución:
Para resolver este problema, debemos determinar dónde está la recta tangente a la gráfica de 4x² + 25y² = 100 en (3, 8/5) que intersecta al eje x. Comience por encontrar dy/dx implícitamente.
Diferenciando, tenemos
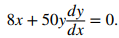
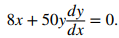
Resolviendo para dy/dx, tenemos
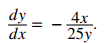
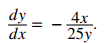
La pendiente de la recta tangente es
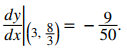
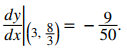
La ecuación de la recta tangente es y = −(3/10)x + 5/2. Para determinar dónde se cruza la recta con el eje x, resuelva 0 = −(3/10)x + 5/2. La solución es x = 25/3. El misil se cruza con el eje x en el punto (25/3, 0).
