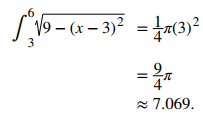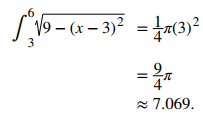| 5. La integral y Técnicas de integración |

5.2 La integral definida: Objetivos de aprendizaje

5.2.1. Indique la definición de la integral definida.
5.2.2. Explicar los términos integrando, límites de integración y variable de integración.
5.2.3. Explica cuándo una función es integrable.
5.2.4. Describa la relación entre la integral definida y el área neta.
5.2.5. Use la geometría y las propiedades de integrales definidas para evaluarlas.
5.2.6. Calcular el valor promedio de una función.

    En la sección anterior definimos el área bajo una curva en términos de sumas de Riemann:

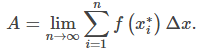
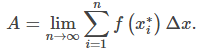
Sin embargo, esta definición vino con restricciones. Requerimos que f (x) fuera continua y no negativa. Lamentablemente, los problemas del mundo real no siempre cumplen con estas restricciones. En esta sección, veremos cómo aplicar el concepto del área bajo la curva a un conjunto más amplio de funciones mediante el uso de la integral definida.

Definición y notación

La integral definida generaliza el concepto del área bajo una curva. Levantamos los requisitos de que f (x) sea continua y no negativa, y definimos la integral definida de la siguiente manera.

DEFINICIÓN 5.2_1. La integral definida

Si f (x) es una función definida en un intervalo [a, b], la integral definida de f de a a b viene dada por siempre que exista el límite. Si este límite existe, se dice que la función f (x) es integrable en [a, b], o es una función integrable.

El símbolo de integral en la definición anterior debería ser familiar. Hemos visto una notación similar en el capítulo sobre Aplicaciones de las derivadas, donde utilizamos el símbolo de la integral indefinida (sin las letras a y b arriba y abajo) para representar una antiderivada. Aunque la notación para integrales indefinidas puede ser similar a la notación para una integral definida, no son lo mismo. Una integral definida es un número. Una integral indefinida es una familia de funciones. Más adelante en este capítulo examinamos cómo se relacionan estos conceptos. Sin embargo, siempre se debe prestar mucha atención a la notación para que sepamos si estamos trabajando con una integral definida o una integral indefinida.

La notación de la integral se remonta a finales del siglo XVII y es una de las contribuciones de Gottfried Wilhelm Leibniz, quien a menudo se considera el codescubridor del cálculo, junto con Isaac Newton. El símbolo de integración ∫ es una S alargada, que sugiere sigma o suma. En una integral definida, arriba y abajo del símbolo de integración están escritas las letras a y b, son los límites del intervalo [a, b]. Los números a y b son x-valores y se denominan límites de integración; específicamente, a es el límite inferior y b es el límite superior. Para aclarar, estamos usando la palabra límite de dos maneras diferentes en el contexto de la integral definida. Primero, hablamos sobre el límite de una suma como n → ∞. En segundo lugar, los límites de la región se denominan límites de integración.

Llamamos a la función f (x) el integrando, y el dx indica que f (x) es una función con respecto a x, llamada variable de integración. Tenga en cuenta que, como el índice en una suma, la variable de integración es una variable ficticia y no tiene ningún impacto en el cálculo de la integral. Podríamos usar cualquier variable que nos guste como variable de integración:

Anteriormente, discutimos el hecho de que si f (x) es continua en [a, b], entonces el límite

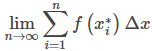
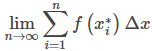
existe y es único. Esto lleva al siguiente teorema, que afirmamos sin pruebas.

TEOREMA 5.2.1. Las funciones continuas son integrables

Si f (x) es continua en [a, b], entonces f es integrable en [a, b].

Las funciones que no son continuas en [a, b] aún pueden ser integrables, dependiendo de la naturaleza de las discontinuidades. Por ejemplo, las funciones con un número finito de discontinuidades de salto en un intervalo cerrado son integrables.

También vale la pena señalar aquí que hemos conservado el uso de una partición regular en las sumas de Riemann. Esta restricción no es estrictamente necesaria. Cualquier partición puede usarse para formar una suma de Riemann. Sin embargo, si se usa una partición no regular para definir la integral definida, no es suficiente tomar el límite ya que el número de subintervalos va al infinito. En cambio, debemos tomar el límite para cuando el ancho del subintervalo más grande tiende a cero. Esto introduce una notación un poco más compleja en nuestros límites y hace que los cálculos sean más difíciles sin realmente obtener mucha información adicional, por lo que nos quedamos con particiones regulares para las sumas de Riemann.

Ejemplo ilustrativo 5.2_1. Evaluar una integral usando la definición

Use la definición de la integral definida para evaluar

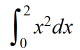
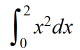
Use una aproximación del punto final derecho para generar la suma de Riemann.

Solución:
Primero debemos establecer una suma de Riemann. Con base en los límites de integración, tenemos a = 0 y b = 2. Para i = 0, 1, 2,…, n, sea P = {xᵢ} una partición regular de [0, 2]. Entonces

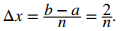
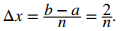
Como estamos utilizando una aproximación del punto final derecho para generar sumas de Riemann, para cada i, necesitamos calcular el valor de la función en el punto final derecho del intervalo [xᵢ₋₁, xᵢ]. El punto final derecho del intervalo es xᵢ], y dado que P es una partición regular,

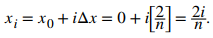
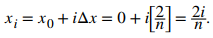
Por lo tanto, el valor de la función en el punto final derecho del intervalo es

Entonces la suma de Riemann toma la forma

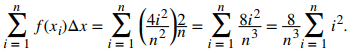
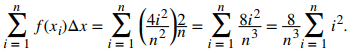
Usando la fórmula de suma para

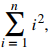
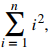
se tiene que

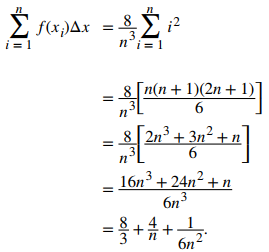
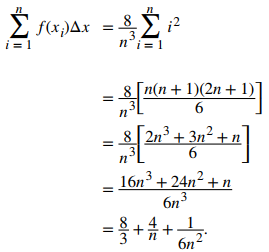
Cómo, para calcular la integral definida, necesitamos tomar el límite cuando n → ∞. Obtenemos

◊

Evaluación de integrales definidas

Evaluar integrales definidas de esta manera puede ser bastante tedioso debido a la complejidad de los cálculos. Más adelante en este capítulo desarrollamos técnicas para evaluar integrales definidas sin tomar límites de sumas de Riemann. Sin embargo, por ahora, podemos confiar en el hecho de que las integrales definidas representan el área bajo la curva, y podemos evaluar integrales definidas mediante el uso de fórmulas geométricas para calcular esa área. Hacemos esto para confirmar que las integrales definidas, de hecho, representan áreas, por lo que podemos discutir qué hacer en el caso de que una curva de una función caiga por debajo del eje x.

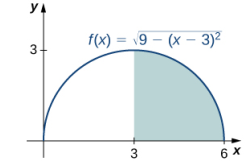
Ejemplo ilustrativo 5.2_2. Uso de fórmulas geométricas para calcular integrales definidas

Use la fórmula para el área de un círculo para evaluar

Solución:
La función describe un semicírculo con radio 3. Para encontrardebemos encontrar el área debajo de la curva sobre el intervalo [3, 6]. La fórmula para el área de un círculo es A = πr². El área de un semicírculo es solo la mitad del área de un círculo, o A = (1/2)πr². El área sombreada en la Figura 5.2_1 cubre la mitad del semicírculo, o A = (1/4)πr². Así,