| 9. Ecuaciones diferenciales | 9.3. Métodos numéricos |

9.3.3 EL MÉTODO RUNGE-KUTTA

      En general, si k es un entero positivo y f satisface las suposiciones apropiadas, existen métodos numéricos con error de truncamiento local O(h^{k + 1}) para resolver un problema de valor inicial

y′ = f(x, y),  y(x₀) = y₀.        (9.3.3.1)

Además, se puede demostrar que un método con error de truncamiento local O(h^{k + 1}) tiene error de truncamiento global O(h^k ). En las Secciones 9.3.1 y 9.3.2 estudiamos métodos numéricos donde k = 1 y k = 2. Omitiremos métodos para los cuales k = 3 y procederemos con el método de Runge-Kutta, el método más utilizado, para el cual k = 4. La magnitud del error de truncamiento local está determinada por la quinta derivada y⁽⁵⁾ de la solución del problema de valor inicial. Por lo tanto, el error de truncamiento local será mayor donde |y⁽⁵⁾| es grande, o menor donde |y⁽⁵⁾| es pequeño. El método de Runge-Kutta calcula valores aproximados y₁, y₂, . . . , y_n de la solución de (9.3.3.1) en x₀, x₀ + h, . . . , x₀ + nh como sigue: Dado y_i, calcule

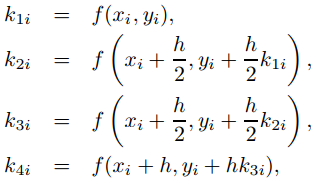
y

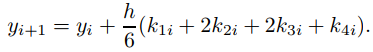
      El siguiente ejemplo, que trata del problema de valor inicial considerado en los Ejemplos 9.3.1.1 y 9.3.2.1, ilustra el procedimiento de cálculo indicado en el método de Runge-Kutta.

Ejemplo 9.3.3.1

Use el método de Runge-Kutta con h = 0.1 para encontrar valores aproximados para la solución del problema de valor inicial

y′ + 2y = x³e^−2x,  y(0) = 1,        (9.3.3.2)

en x = 0.1, 0.2.

Solución:

Reescribimos (9.3.3.2) como

y′  = − 2y + x³e^−2x,  y(0) = 1, 

que es de la forma (9.3.3.1), con

f(x, y) = − 2y + x³e^−2x,  x₀ = 0  y  y₀ = 1.

      El método de Runge-Kutta produce

♦

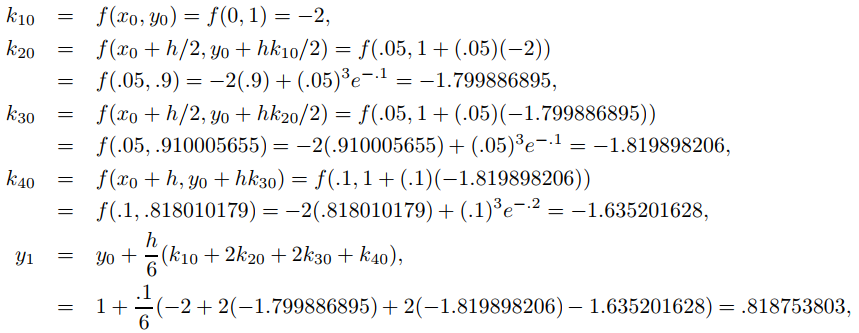
      El método de Runge-Kutta es suficientemente preciso para la mayoría de las aplicaciones.

Ejemplo 9.3.3.2

La Tabla 9.3.3.1 muestra los resultados de usar el método de Runge-Kutta con tamaños de paso h = 0.1 y h = 0.05 para encontrar valores aproximados de la solución del problema de valor inicial

y′ + 2y = x³e^−2x,  y(0) = 1,

en x = 0, 0.1, 0.2, 0.3, . . . , 1.0. A modo de comparación, también muestra los valores aproximados correspondientes obtenidos con el método de Euler mejorado en el Ejemplo 9.3.2.2, y los valores de la solución exacta

Tabla 9.3.3.1. Solución numérica de y′ + 2y = x³e^−2x,  y(0) = 1, por el método de Runge-Kuttta y el método de Euler mejorado.

Los resultados obtenidos por el método de Runge-Kutta son claramente mejores que los obtenidos por el método de Euler mejorado; los resultados obtenidos por el método de Runge-Kutta con h = 0,1 son mejores que los obtenidos por el método de Euler mejorado con h = 0,05.  ♦

Ejemplo 9.3.3.3

La tabla 9.3.3.2 muestra resultados análogos para el problema de valor inicial no lineal

y′ = −2y² + xy + x²,  y(0) = 1.

Aplicamos el método de Euler mejorado a este problema en el Ejemplo 9.3.2.3.

Tabla 9.3.3.2. Solución numérica de y′ = −2y² + xy + x², y(0) = 1, por el método de Runge-Kuttta y el método de Euler mejorado.

Ejemplo 9.3.3.4

Las tablas 9.3.3.3 y 9.3.3.4 muestran los resultados obtenidos al aplicar los métodos semilineales de Runge-Kutta y Runge-Kutta al problema de valor inicial

y′ − 2xy = 1,  y(0) = 3,

Lo que consideramos en los Ejemplos 9.3.1.4 y 9.3.2.4.

Tabla 9.3.3.3. Solución numérica de y′ − 2xy = 1,  y(0) = 3, por el método de Runge-Kutta.

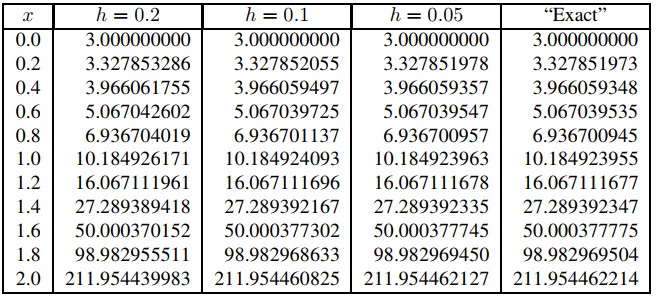
Tabla 9.3.3.4. Solución numérica de y′ − 2xy = 1,  y(0) = 3, por el método semilineal de Runge-Kutta.

El caso en el que x₀ no es el extremo izquierdo

Hasta ahora en este capítulo hemos considerado métodos numéricos para resolver un problema de valor inicial

y′ = f(x, y),  y(x₀) = y₀        (9.3.3.3)

en un intervalo [x₀, b], para el cual x₀ es el extremo izquierdo. No hemos discutido métodos numéricos para resolver (9.3.3.3) en un intervalo [a,x₀], para el cual x₀ es el extremo derecho. Para ser específicos, ¿cómo podemos obtener valores aproximados y₋₁, y₋₂, . . . , y_−n de la solución de (9.3.3.3) en x₀ − h, . . ., x₀ − nh, donde h = (x₀ − a)/n? Aquí está la respuesta a esta pregunta:

      Considere el problema del valor inicial

z′ = −f(−x, z),  z(−x₀) = y₀,        (9.3.3.4)

en el intervalo [−x₀, −a], para el cual −x₀ es el extremo izquierdo. Use un método numérico para obtener valores aproximados z₁, z₂, . . . , z_n de la solución de (9.3.3.4) en −x₀ + h, −x₀ + 2h, . . . , −x₀ + x₀ = −a. Entonces

y₋₁ = z₁, y₋₂ = z₂, . . ., y_−n = z_n son valores aproximados de la solución de (9.3.3.3) en x₀ − h, x₀ − 2h, . . . , x₀ − nh = a.

      La justificación de esta respuesta se esboza en el ejercicio 23. Observe lo fácil que es hacer el cambio del problema dado (9.3.3.3) al problema modificado (9.3.3.4): primero reemplace f por −f y luego reemplace x, x₀ , y y por −x, −x₀ y z, respectivamente.

Ejemplo 9.3.3.5

Use el método de Runge-Kutta con tamaño de paso h = 0.1 para encontrar valores aproximados de la solución de

(y − 1)²y′ = 2x + 3,  y(1) = 4        (9.3.3.5)

en x = 0, 0.1, 0.2, . . . , 1.

Solución:

Primero reescribimos (9.3.3.5) en la forma (9.3.3.3) como

      (9.3.3.6)

Dado que la condición inicial y(1) = 4 se impone en el extremo derecho del intervalo [0, 1], aplicamos el método de Runge-Kutta al problema de valor inicial

      (9.3.3.7)

en el intervalo [−1, 0]. (Debe verificar que (9.3.3.7) está relacionado con (9.3.3.6) como (9.3.3.4) está relacionado con (9.3.3.3).) La tabla 9.3.3.5 muestra los resultados. Invirtiendo el orden de las filas en la Tabla 9.3.3.5 y cambiando los signos de los valores de x se obtienen las dos primeras columnas de la Tabla 9.3.3.6. La última columna de la Tabla 9.3.3.6 muestra los valores exactos de y, que están dados por

y = 1 + (3x² + 9x + 15)^1/3.

(Dado que la ecuación diferencial en (9.3.3.6) es separable, esta fórmula se puede obtener por el método de la Sección 9.2.2.)

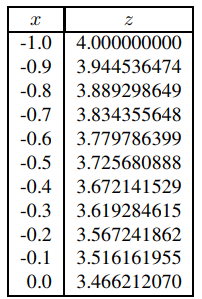
Tabla 9.3.3.5. Solución numérica de ,  en [−1, 0].

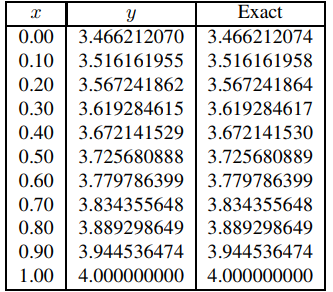
Tabla 9.3.3.6. Solución numérica de y = 1 + (3x² + 9x + 15)^1/3,  y(1) = 4, en [0, 1].

      Le dejamos a usted desarrollar un procedimiento para manejar la solución numérica de (9.3.3.3) en un intervalo [a, b] tal que a < x₀ < b (Ejercicios 26 y 27).