| 6.4 Longitud de arco de una curva y área de una superficie |

Ejercicios propuestos para el Capítulo 6.4

Para los siguientes ejercicios, encuentre la longitud de las funciones sobre el intervalo dado:

165. \(y = 5x\) desde \(x = 0\) hasta \(x = 2\)

166. \(y = -\frac{1}{2}x + 25\) desde \(x = 1\) hasta \(x = 4\)

167. \(x = 4y\) desde \(y = -1\) hasta \(y = 1\)

168. Elija una función lineal arbitraria \(x = g(y)\) sobre cualquier intervalo de su elección \((y_1, y_2)\). Determine la longitud de la función y luego pruebe que la longitud es correcta usando geometría.

169. Encuentre el área de la superficie del volumen generado cuando la curva \(y = \sqrt{x}\) gira alrededor del eje x desde \((1, 1)\) hasta \((4, 2)\), como se ve aquí.

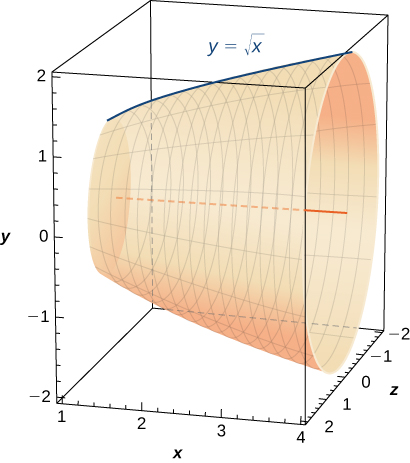
170. Encuentre el área de la superficie del volumen generado cuando la curva \(y = x^2\) gira alrededor del eje y desde \((1, 1)\) hasta \((3, 9)\).

Para los siguientes ejercicios, encuentre las longitudes de las funciones de x sobre el intervalo dado. Si no puede evaluar la integral exactamente, utilice tecnología para aproximarla.

171. \(y = x^{3/2}\) desde \((0, 0)\) hasta \((1, 1)\)

172. \(y = x^{2/3}\) desde \((1, 1)\) hasta \((8, 4)\)

173. \(y = \frac{1}{3}(x^2 + 2)^{3/2}\) desde \(x = 0\) hasta \(x = 1\)

174. \(y = \frac{1}{3}(x^2 – 2)^{3/2}\) desde \(x = 2\) hasta \(x = 4\)

175. [T] \(y = e^x\) en \(x = 0\) hasta \(x = 1\)

176. \(y = \frac{x^3}{3} + \frac{1}{4x}\) desde \(x = 1\) hasta \(x = 3\)

177. \(y = \frac{x^4}{8} + \frac{1}{4x^2}\) desde \(x = 1\) hasta \(x = 2\)

178. \(y = \frac{2x^{3/2}}{3} – \frac{x^{1/2}}{2}\) desde \(x = 1\) hasta \(x = 4\)

179. \(y = \frac{1}{27}(9x^2 + 6)^{3/2}\) desde \(x = 0\) hasta \(x = 2\)

180. [T] \(y = \sin x\) en \(x = 0\) hasta \(x = \pi\)

Para los siguientes ejercicios, encuentra las longitudes de las funciones de \( y \) sobre el intervalo dado. Si no puedes evaluar la integral exactamente, usa tecnología para aproximarla:

181. \( y = \frac{5-3x}{4} \) desde \( y = 0 \) hasta \( y = 4 \)
182. \( x = \frac{1}{2}(e^y + e^{-y}) \) desde \( y = -1 \) hasta \( y = 1 \)
183. \( x = 5y^{3/2} \) desde \( y = 0 \) hasta \( y = 1 \)
184. [T] \( x = y^2 \) desde \( y = 0 \) hasta \( y = 1 \)
185. \( x = \sqrt{y} \) desde \( y = 0 \) hasta \( y = 1 \)
186. \( x = \frac{2}{3}(y^2 + 1)^{3/2} \) desde \( y = 1 \) hasta \( y = 3 \)
187. [T] \( x = \tan y \) desde \( y = 0 \) hasta \( y = \frac{3}{4} \)
188. [T] \( x = \cos^2 y \) desde \( y = -\frac{\pi}{2} \) hasta \( y = \frac{\pi}{2} \)
189. [T] \( x = 4^y \) desde \( y = 0 \) hasta \( y = 2 \)
190. [T] \( x = \ln(y) \) en \( y = \frac{1}{e} \) hasta \( y = e \)

Para los siguientes ejercicios, encuentra el área de la superficie del volumen generado cuando las siguientes curvas giran alrededor del eje *x*. Si no puedes evaluar la integral exactamente, usa tu calculadora para aproximarla:

191. \( y = \sqrt{x} \) desde \( x = 2 \) hasta \( x = 6 \)
192. \( y = x^3 \) desde \( x = 0 \) hasta \( x = 1 \)
193. \( y = 7x \) desde \( x = -1 \) hasta \( x = 1 \)
194. [T] \( y = \frac{1}{x^2} \) desde \( x = 1 \) hasta \( x = 3 \)
195. \( y = \sqrt{4 – x^2} \) desde \( x = 0 \) hasta \( x = 2 \)
196. \( y = \sqrt{4 – x^2} \) desde \( x = -1 \) hasta \( x = 1 \)
197. \( y = 5x \) desde \( x = 1 \) hasta \( x = 5 \)
198. [T] \( y = \tan x \) desde \( x = -\frac{\pi}{4} \) hasta \( x = \frac{\pi}{4} \)

Para los siguientes ejercicios, encuentra el área de la superficie del volumen generado cuando las siguientes curvas giran alrededor del eje *y*. Si no puedes evaluar la integral exactamente, usa tu calculadora para aproximarla:

199. \( y = x^2 \) desde \( x = 0 \) hasta \( x = 2 \)
200. \( y = \frac{1}{2}x^2 + \frac{1}{2} \) desde \( x = 0 \) hasta \( x = 1 \)
201. \( y = x + 1 \) desde \( x = 0 \) hasta \( x = 3 \)
202. [T] \( y = \frac{1}{x} \) desde \( x = \frac{1}{2} \) hasta \( x = 1 \)
203. \( y = \sqrt[3]{x} \) desde \( x = 1 \) hasta \( x = 27 \)
204. [T] \( y = 3x^4 \) desde \( x = 0 \) hasta \( x = 1 \)
205. [T] \( y = \frac{1}{\sqrt{x}} \) desde \( x = 1 \) hasta \( x = 3 \)
206. [T] \( y = \cos x \) desde \( x = 0 \) hasta \( x = \frac{\pi}{2} \)
207. La base de una lámpara se construye girando un cuarto de círculo \( y = \sqrt{2x – x^2} \) alrededor del eje *y* desde \( x = 1 \) hasta \( x = 2 \), como se ve aquí. Crea una integral para el área de la superficie de esta curva y calcúlala.

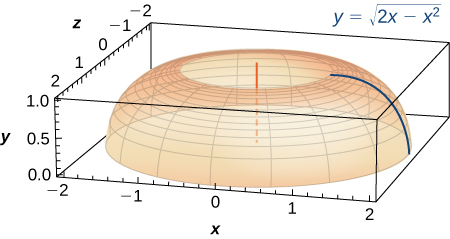
208. Una bombilla tiene la forma de una esfera con un radio de \( \frac{1}{2} \) pulgada, con la parte inferior cortada para encajar exactamente en un cilindro de radio \( \frac{1}{4} \) pulgada y longitud \( \frac{1}{3} \) pulgada, como se ve aquí. La esfera se corta en la parte inferior para encajar exactamente en el cilindro, por lo que el radio del corte es \( \frac{1}{4} \) pulgada. Encuentra el área de la superficie (sin incluir la parte superior ni la inferior del cilindro).

209. [T] Una pantalla de lámpara se construye rotando \( y = \frac{1}{x} \) alrededor del eje *x* desde \( y = 1 \) hasta \( y = 2 \), como se ve aquí. Determina cuánto material necesitarías para construir esta pantalla de lámpara, es decir, el área de la superficie, con una precisión de cuatro decimales.

210. [T] Un ancla se arrastra detrás de un bote de acuerdo con la función \( y = 24e^{-x^2/2} – 24 \), donde \( y \) representa la profundidad debajo del bote y \( x \) es la distancia horizontal del ancla desde la parte trasera del bote. Si el ancla está a 23 pies por debajo del bote, ¿cuánta cuerda tienes que tirar para alcanzar el ancla? Redondea tu respuesta a tres decimales.
211. [T] Estás construyendo un puente que abarcará 10 pies. Tienes la intención de agregar una cuerda decorativa con la forma de \( y = 5|\sin((x\pi)/5)| \), donde \( x \) es la distancia en pies desde un extremo del puente. Averigua cuánta cuerda necesitas comprar, redondeado al pie más cercano.

Para los siguientes ejercicios, encuentra la longitud exacta del arco para los siguientes problemas sobre el intervalo dado:

212. \( y = \ln(\sin x) \) desde \( x = \pi/4 \) hasta \( x = (3\pi)/4 \). (Pista: Recuerda las identidades trigonométricas).
213. Dibuja las gráficas de \( y = x^2 \), \( y = x^6 \) y \( y = x^{10} \). Para \( y = x^n \), a medida que \( n \) aumenta, formula una predicción sobre la longitud del arco desde (0, 0) hasta (1, 1). Ahora, calcula las longitudes de estas tres funciones y determina si tu predicción es correcta.
214. Compara las longitudes de la parábola \( x = y^2 \) y la línea \( x = by \) desde (0, 0) hasta \( (b^2, b) \) a medida que \( b \) aumenta. ¿Qué observas?
215. Resuelve para la longitud de \( x = y^2 \) desde (0, 0) hasta (1, 1). Muestra que \( x = (1/2)y^2 \) desde (0, 0) hasta (2, 2) es dos veces más largo. Grafica ambas funciones y explica por qué esto es así.
216. [T] ¿Cuál es más largo entre (1, 1) y (2, 1/2): la hipérbola \( y = 1/x \) o la gráfica de \( x + 2y = 3 \)?
217. Explica por qué el área de la superficie es infinita cuando \( y = 1/x \) se gira alrededor del eje *x* para \( 1 \leq x < \infty \), pero el volumen es finito.