| 7. Sucesiones y series infinitas |
7.1 SUCESIONES: Objetivos de aprendizaje
7.1.1. Encontrar la fórmula para el término general de una sucesión.
7.1.2. Calcular el límite de una sucesión si existe.
7.1.3. Determinar la convergencia o divergencia de una sucesión dada.
En esta sección, presentamos sucesiones (secuencias) y definimos lo que significa que una secuencia converja o diverja. Mostramos cómo encontrar límites de secuencias que convergen, a menudo utilizando las propiedades de límites para las funciones discutidas anteriormente. Cerramos esta sección con el Teorema de la convergencia monótona, una herramienta que podemos usar para demostrar que ciertos tipos de sucesiones convergen.
Terminología de sucesiones
Para comenzar a trabajar con este nuevo tema, necesitamos algunos términos y definiciones. Primero, una sucesión infinita es una lista ordenada de números de la forma


Cada uno de los números en la sucesión se llama término. El símbolo n se llama índice variable para la sucesión. Usamos la notación


para denotar esta sucesión. Se utiliza una notación similar para los conjuntos, pero una sucesión es una lista ordenada, mientras que un conjunto no está ordenado. Debido a que existe un número particular a para cada entero positivo n, también podemos definir una sucesión como una función cuyo dominio es el conjunto de enteros positivos.
Consideremos la lista ordenada infinita
2, 4, 8, 16, 32, …
Esta es una sucesión en la que los términos primero, segundo y tercero están dados por a1 = 2, a2 = 4 y a3 = 8. Probablemente pueda ver que los términos en esta sucesión tienen el siguiente patrón:
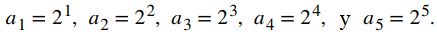
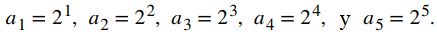
Suponiendo que este patrón continúa, podemos escribir el enésimo término en la sucesión mediante la fórmula explícita
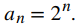
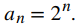
Usando esta fórmula, podemos escribir esta secuencia como
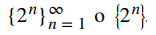
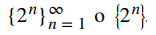
Alternativamente, podemos describir esta sucesión de una manera diferente. Como cada término es dos veces el término anterior, esta sucesión se puede definir de forma recursiva expresando el enésimo término an en función del término anterior an − 1. En particular, podemos definir esta secuencia como la sucesión { an } donde a1 = 2 y para todo n ≥ 2, cada término an está definido por la relación de recurrencia an = 2an − 1.
Definición 7.1.1. Sucesión infinita
|
Una sucesión infinita {an} es una lista ordenada de números de la forma a1, a2, a3, … , an, … El subíndice n se denomina índice variable de la sucesión. Cada número an es un término de la sucesión. A veces, las sucesiones se definen mediante fórmulas explícitas, en cuyo caso an = f (n) para alguna función f (n) definida sobre los enteros positivos. En otros casos, las sucesiones se definen mediante el uso de una relación de recurrencia. En una relación de recurrencia, un término (o más) de la secuencia se da explícitamente, y los términos posteriores se definen a partir de términos anteriores de la sucesión |
Tenga en cuenta que el índice no tiene que comenzar en n = 1, podría comenzar con otro entero. Por ejemplo, una sucesión dada por la fórmula explícita an = f (n) podría comenzar en n = 0, en cuyo caso la secuencia sería a0, a1, a2, …
De manera similar, para una secuencia definida por una relación de recurrencia, el término a₀ puede darse explícitamente, y los términos an para n ≥ 1 pueden definirse en términos de an − 1. Como una secuencia {an} tiene exactamente un valor para cada entero positivo n, puede describirse como una función cuyo dominio es el conjunto de enteros positivos. Como resultado, tiene sentido discutir acerca de la gráfica de una sucesión. La gráfica de una secuencia {an} consiste en todos los puntos (n, an) para todos los enteros positivos n. La figura 7.1_1 muestra la gráfica de {2n}.

(Figura 7.1_1 Los puntos trazados representan una gráfica de la sucesión {2ⁿ}.)
Sucesiones aritméticas y geométricas
Dos tipos de sucesiones ocurren con frecuencia y reciben nombres especiales: sucesiones aritméticas y sucesiones geométricas.
◊ En una sucesión aritmética, la diferencia entre cada par de términos consecutivos es la misma. Por ejemplo, considere la sucesión
3, 7, 11, 15, 19,….
Puede ver que la diferencia entre cada par de términos consecutivos es 4. Suponiendo que este patrón continúe, esta secuencia es una sucesión aritmética. Se puede describir esta sucesión utilizando la relación de recurrencia


Tenga en cuenta que


Por lo tanto, la secuencia también se puede describir utilizando la fórmula explícita
![]()
![]()
En general, una sucesión aritmética es cualquier secuencia de la forma
![]()
![]()
◊ En una sucesión geométrica, la razón de cada par de términos consecutivos es la misma. Por ejemplo, considere la secuencia
![]()
![]()
Vemos que la razón de cualquier término al término precedente es −1/3. Suponiendo que este patrón continúa, esta secuencia es una sucesión geométrica. Se puede definir recursivamente como


Alternativamente, dado que


la secuencia se puede describir usando la fórmula explícita


La secuencia {2n} que discutimos anteriormente es una sucesión geométrica, donde la razón de cualquier término al término anterior es 2.
En general, una sucesión geométrica es cualquier secuencia de la forma
![]()
![]()
EJEMPLO ILUSTRATIVO 7.1_1. Encontrar fórmulas explícitas para dos sucesiones
Para cada una de las siguientes secuencias, encuentre una fórmula explícita para el enésimo término de la secuencia.


Solución:
a. Primero, tenga en cuenta que los términos de la secuencia se alternan de negativos a positivos. Los términos impares en la secuencia son negativos y los términos pares son positivos. Por lo tanto, el enésimo término incluye un factor de (−1)n. Luego, considere la secuencia de numeradores {1, 2, 3, …} y la secuencia de denominadores {2, 3, 4, …}. Podemos ver que ambas secuencias son secuencias aritméticas. El enésimo término en la secuencia de numeradores es n, y el enésimo término en la secuencia de denominadores es n + 1. Por lo tanto, la secuencia se puede describir mediante la fórmula explícita


b. La secuencia de numeradores 3, 9, 27, 81, 243, … es una secuencia geométrica. El numerador del enésimo término es 3n. La secuencia de denominadores 4, 7, 10, 13, 16, … es una secuencia aritmética. El denominador del enésimo término es 4 + 3 (n − 1) = 3n + 1. Por lo tanto, podemos describir la secuencia mediante la fórmula explícita


Ejercicio de control 7.1_1
Encuentre una fórmula explícita para el enésimo término de la secuencia {1/5, −1/7, 1/9, −1/11,…}.
EJEMPLO ILUSTRATIVO 7.1_2. Sucesión definida por relaciones de recurrencia
Para cada una de las siguientes secuencias definidas recursivamente, encuentre una fórmula explícita para la secuencia.
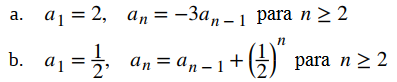
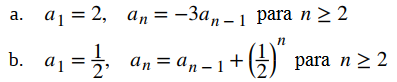
Solución:
a. Escribiendo los primeros términos, tenemos


En general,![]()
![]()


De este patrón, deducimos la fórmula explícita


Ejercicio de control 7.1_2
Encuentre una fórmula explícita para la secuencia definida recursivamente tal que
a1 = −4 y an = an − 1 + 6.

Gracias por compartir sus conocimientos sobre este tema clave. Saludos mi profe |