6. Aplicaciones de la integral
- 6.6 Momentos y centros de masa
- 6.7 Integrales, funciones exponenciales y logaritmos
- 6.8 Crecimiento exponencial y decadencia
- 6.9 Cálculo de las funciones hiperbólicas
La presa Hoover es una maravilla de la ingeniería. Cuando el lago Mead, el embalse detrás de la presa, está lleno, la presa soporta una gran fuerza. Sin embargo, los niveles de agua en el lago varían considerablemente como resultado de las sequías y las distintas demandas de agua. Más adelante en este capítulo, usamos integrales definidas para calcular la fuerza ejercida sobre la presa cuando el depósito está lleno y examinamos cómo los niveles de agua cambiantes afectan esa fuerza (vea el ejemplo 6.28).
La fuerza hidrostática es solo una de las muchas aplicaciones de integrales definidas que exploramos en este capítulo. Desde aplicaciones geométricas como área de superficie y volumen, hasta aplicaciones físicas como masa y trabajo, hasta modelos de crecimiento y decadencia, las integrales definidas son una herramienta poderosa para ayudarnos a comprender y modelar el mundo que nos rodea.
Miscelánea de ejercicios resueltos del capítulo 6
1. Determine el área de la región limitada por las curvas y = x3 + 1, x – y + 1 = 0
Solución – Juan Beltrán:
Despejamos y en la segunda ecuación, renombramos las funciones, trazamos las gráficas de las funciones y mostramos la región cuya área vamos a calcular
y = f (x) = x3 + 1, g(x) = x + 1
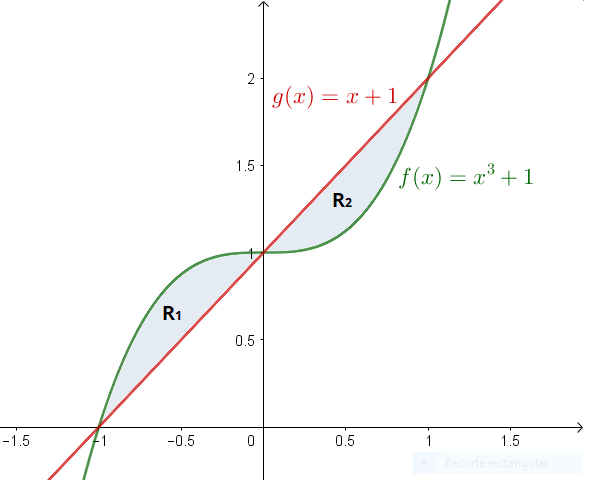

El área de la región es R = R1 + R2.
Igualamos las fórmulas de las funciones para deducir donde se intersecan


Observamos que en el intervalo [−1, 0], f (x) ≥ g(x), y en el intervalo [0, 1], g(x) ≥ f (x); de tal modo que el área de la región R está dada por,


2. Determine el área de la región limitada por las curvas 4x = y2, 4x + y – 6 = 0
Solución – Juan Beltrán:
Trazamos las gráficas de las curvas y destacamos la región R cuya área nos proponemos calcular


Para facilitar los cálculos, vamos a integrar respecto del eje y. Despejamos x en ambas ecuaciones
x = y2/4 y x = 3/2 – y/4
Para hallar los puntos donde se cruzan las gráficas de estas curvas, igualamos los miembros derechos y resolvemos la ecuación resultante para y
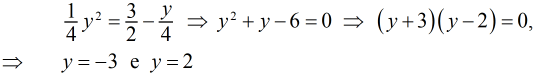
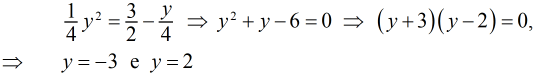
Observamos que la gráfica de 4x + y – 6 = 0 se encuentra siempre a la derecha de la gráfica de 4x = y2 en el intervalo [–3, 2], por lo que al integrar con respecto a la variable y, el área de la región está dada por


3. Aproxime por la regla de Simpson el valor de la integral 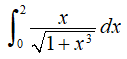
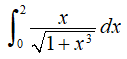
Solución – Juan Beltrán:
Una aproximación de una integral definida en un intervalo cerrado [a, b], aplicando la regla de Simpson está dada por la siguiente suma finita de n + 1 términos


donde n es un entero positivo par y Δx = (b − a)/n.
Los valores particulares de a, b y n en el presente ejercicio son a = 0, b = 2 y n = 6, con Δx = (2 − 0)/6 = 1/3 y los puntos extremos de los intervalos son x0 = 0, x1 = 1/3, x2 = 2/3, x3 = 1, x4 = 4/3, x5 = 5/3, x6 = 2, sustituyendo estos valores en la fórmula, se obtiene

Como f (x) = x/√(1+ x3), tenemos que (con cinco cifras decimales de aproximación)
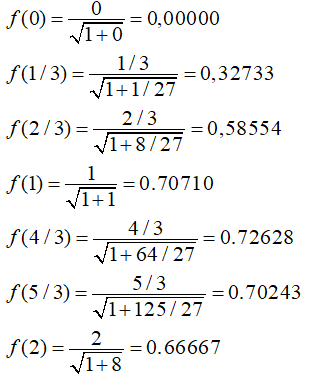
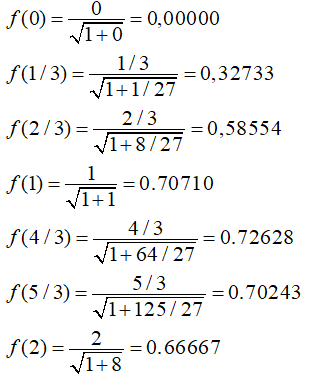
Sustituyendo estos valores en la fórmula para S6, se obtiene


4. Aproxime por la regla del trapecio el valor de la integral

Solución – Juan Beltrán:
Una aproximación de una integral definida en un intervalo cerrado [a, b], aplicando la regla del trapecio está dada por la siguiente suma finita de n + 1 términos


Los valores particulares de a, b y n en el presente ejercicio son a = 0, b = π/2 y n = 5, con Δx = (π/2 − 0)/5 = π/10 y los puntos extremos de los intervalos son x0 = 0, x1 = π/10, x2 = π/5, x3 = 3π/10, x4 = 2π/5, x5 = π/2, sustituyendo estos valores en la fórmula, se obtiene

Como f (x) = senx2, tenemos que (con cinco cifras decimales de aproximación)

Sustituyendo estos valores en la fórmula para T5, se obtiene
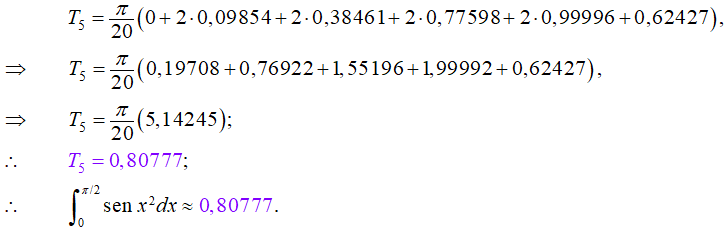

5. Determine el volumen del sólido de revolución que se obtiene al hacer girar alrededor del eje x el área limitada por la curva x2 + y2 = 9 y la recta y − 1 = 0.
Solución – Juan Beltrán:
