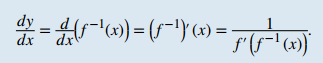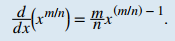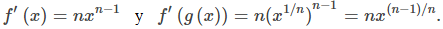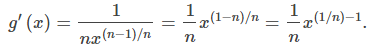Derivadas de funciones inversas

Derivadas de funciones inversas: Objetivos de aprendizaje

3.7.1. Calcular la derivada de una función inversa.
3.7.2. Reconocer las derivadas de las funciones trigonométricas inversas estándar.

    En esta sección exploramos la relación entre la derivada de una función y la derivada de su inversa. Para funciones cuyas derivadas ya conocemos, podemos usar esta relación para encontrar derivadas de inversas sin tener que usar la definición de límite de la derivada. En particular, aplicaremos la fórmula para derivadas de funciones inversas a funciones trigonométricas. Esta fórmula también se puede usar para extender la regla de la potencia a exponentes racionales.

La derivada de una función inversa

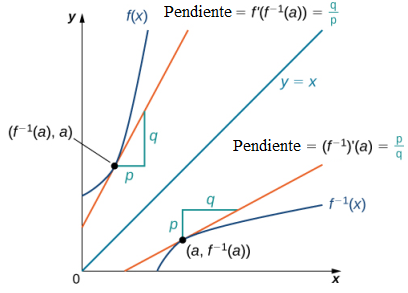
Comenzamos considerando una función y su inversa. Si f (x) es tanto invertible como diferenciable, parece razonable que la inversa de f (x) también sea diferenciable. La figura 3.7_1 muestra la relación entre una función f (x) y su inversa f ⁻¹(x). Mire el punto (a,  f ⁻¹(a)) en la gráfica de f ⁻¹(x) que tiene una recta tangente con una pendiente de (f ⁻¹)′(a) = p/q. Este punto corresponde a un punto (f ⁻¹(a), a) en la gráfica de f (x) que tiene una recta tangente con una pendiente de f ′(f ⁻¹(a)) = q/p. Por lo tanto, si f ⁻¹(x) es diferenciable en a, entonces debe ser el caso que

También podemos deducir la fórmula para la derivada de la inversa al recordar primero que x = f (f ⁻¹(x)). Luego, al diferenciar ambos lados de esta ecuación (usando la regla de la cadena a la derecha), obtenemos

Resolviendo para (f ⁻¹)′(x), obtenemos

Resumimos este resultado en el siguiente teorema.

TEOREMA 3.7.1. Teorema de la función inversa

Sea f (x) una función que es tanto invertible como diferenciable. Sea y = f ⁻¹(x) la inversa de f (x). Para todos los x que satisfacen f ′(f ⁻¹(x)) ≠ 0, Alternativamente, si y = g(x) es la inversa de f (x), entonces

Ejemplo ilustrativo 3.7_1. Aplicación del teorema de la función inversa

Usa el teorema de la función inversa para encontrar la derivada de g(x) = (x + 2)/x. Compare la derivada resultante con la obtenida diferenciando la función directamente.

Solución:

El inverso de g(x) = (x + 2)/x es f (x) = 2/(x − 1). Como g′(x) = 1/ f ′(g(x)), comience por encontrar f ′(x). Así,

Finalmente,

Podemos verificar que esta es la derivada correcta aplicando la regla del cociente a g(x) para obtener◊

Ejemplo ilustrativo 3.7_2. Aplicación del teorema de la función inversa

Usa el teorema de la función inversa para encontrar la derivada de 

Solución:

La función g(x) = ³√x es la inversa de la función f (x) = x³. Como g′(x) = 1/ f ′(g(x)), comience por encontrar f ′(x). De donde,

Finalmente, ◊

Del ejemplo anterior, vemos que podemos usar el teorema de la función inversa para extender la regla de la potencia a exponentes de la forma 1/n, donde n es un número entero positivo. Esta extensión finalmente nos permitirá diferenciar x^q, donde q es cualquier número racional.

TEOREMA 3.7.2. Extendiendo la regla de la potencia a exponentes racionales

La regla de la potencia puede extenderse a exponentes racionales. Es decir, si n es un número entero positivo, entonces Además, si n es un número entero positivo y m es un número entero arbitrario, entonces

Prueba La función g(x) = x¹ˡ ⁿ es la inversa de la función f (x) = xⁿ. Como g′(x) = 1/ f ′(g(x)), comience por encontrar f ′(x). Así,Finalmente, Para diferenciar xᵐ ˡ ⁿ debemos reescribir como (x¹ˡ ⁿ)ᵐ y aplicar la regla de la cadena. Así, ◊

Ejemplo ilustrativo 3.7_3. Aplicando la Regla de la potencia a una potencia Racional

Encuentre la ecuación de la recta tangente a la gráfica de y = x²ˡ ³ en x = 8.

Solución:

Primero encuentre dy/dx y evalúa en x = 8. Ya que

la pendiente de la recta tangente a la gráfica en x = 8 es 13.
Sustituyendo x = 8 en la función original, obtenemos y = 4. Así, la recta tangente pasa por el punto (8, 4). Sustituyendo en la fórmula punto-pendiente de una recta, obtenemos la ecuación de la recta tangente

◊

Derivadas de funciones trigonométricas inversas

Ahora dirigimos nuestra atención a encontrar derivadas de funciones trigonométricas inversas. Estas derivadas resultarán invaluables en el estudio de la integración más adelante en este texto. Las derivadas de funciones trigonométricas inversas son bastante sorprendentes porque sus derivadas son en realidad funciones algebraicas. Anteriormente, las derivadas de funciones algebraicas han demostrado ser funciones algebraicas y las derivadas de funciones trigonométricas han demostrado ser funciones trigonométricas. Aquí, por primera vez, vemos que la derivada de una función no necesita ser del mismo tipo que la función original.

Ejemplo ilustrativo 3.7_4. Derivada de la función seno inversa

Usa el teorema de la función inversa para encontrar la derivada de g(x) = sen⁻¹x.

Solución:

Dado que para x en el intervalo [−π/2,  π/2], f (x) = senx es el inverso de g(x) = sen⁻¹x, comience por encontrar f ′(x). Ya que

Observamos que

Análisis

Para ver que cos( sen⁻¹x) = √(1 − x²), considere el siguiente argumento. Establezca sen⁻¹x = θ. En este caso, senθ = x donde −π/2 ≤ θ ≤π/2. Comenzamos considerando el caso donde 0 < θ < π/2. Como θ es un ángulo agudo, podemos construir un triángulo rectángulo que tenga un ángulo agudo θ, una hipotenusa de longitud 1 y el ángulo opuesto lateral θ que tenga una longitud x. Según el teorema de Pitágoras, el lado adyacente al ángulo θ tiene una longitud de √(1 − x²). Este triángulo se muestra en la figura 3.7_2. Usando el triángulo, vemos que cos(sen⁻¹x) = cosθ = √(1 − x²).

Figura 3.7_2 Usando un triángulo rectángulo con ángulo agudo θ, una hipotenusa de longitud 1 y el lado opuesto al ángulo θ con longitud x, podemos ver que cos(sen⁻¹x) = cosθ = √(1 − x²).

En el caso donde −π/2 < θ < 0, hacemos la observación de que 0 <−θ < π/2 y por lo tanto

Ahora si θ = π/2 o θ = −π/2, x = 1 o x = −1, y dado que en cualquier caso cosθ = 0 y √(1 − x²) = 0, tenemos

En consecuencia, en todos los casos, cos( sen⁻¹x) = √(1 − x²). ◊

Ejemplo ilustrativo 3.7_5. Aplicación de la regla de la cadena a la función seno inversa

Aplique la regla de la cadena a la fórmula deducida en el ejemplo 3.7_2 para encontrar la derivada de h(x) = sen⁻¹(g(x)) y use este resultado para encontrar la derivada de h(x) = sen⁻¹ (2x³) .

Solución:

Aplicando la regla de la cadena a h(x) = sen⁻¹(g(x)), tenemos

Ahora deje que g(x) = 2x³, entonces g′(x) = 6x². Sustituyendo en el resultado anterior, obtenemos

◊