| 8. Ecuaciones paramétricas y coordenadas polares | |Ejercicios propuestos del Capítulo 8.1 |
8.1 Ecuaciones paramétricas
Objetivos de aprendizaje:
8.1.1. Trazar una curva descrita por ecuaciones paramétricas.
8.1.2. Convertir las ecuaciones paramétricas de una curva en la forma y = f (x).
8.1.3. Reconocer las ecuaciones paramétricas de curvas básicas, como una recta y una circunferencia.
8.1.4. Reconocer las ecuaciones paramétricas de la cicloide.
En esta sección examinamos las ecuaciones paramétricas y sus gráficas. En el sistema de coordenadas bidimensional, las ecuaciones paramétricas son útiles para describir curvas que no son necesariamente funciones. El parámetro es una variable independiente de la que dependen tanto la variable x como la variable y, y a medida que aumenta el parámetro, los valores de x e y trazan una ruta a lo largo de una curva plana. Por ejemplo, si el parámetro es t (una opción común), entonces t podría representar el tiempo. De tal manera que x e y se definen como funciones del tiempo t, y el conjunto de puntos (x(t), y(t)) puede describir la posición en el plano de un objeto dado a medida que se mueve a lo largo de una trayectoria curva.
Ecuaciones paramétricas y sus gráficas
Considere la órbita de la Tierra alrededor del Sol. Nuestro año dura aproximadamente 365.25 días, pero para esta discusión usaremos 365 días. El 1 de enero de cada año, la ubicación física de la Tierra con respecto al Sol es casi la misma, excepto en los años bisiestos, cuando el retraso introducido por 1/4 de día adicional de tiempo en órbita está incorporado en el calendario. Llamamos al 1 de enero “día 1” del año. Entonces, por ejemplo, el día 31 es el 31 de enero, el día 59 es el 28 de febrero, y así sucesivamente.
El número del día en un año puede considerarse una variable que determina la posición de la Tierra en su órbita. A medida que la Tierra gira alrededor del Sol, su ubicación física cambia en relación con el Sol. Después de un año completo, estamos de vuelta donde comenzamos, e inicia un nuevo año. De acuerdo con las leyes de Kepler sobre el movimiento planetario, la forma de la órbita es elíptica, con el Sol en un foco de la elipse. Estudiamos esta idea con más detalle en el capítulo sobre secciones cónicas.
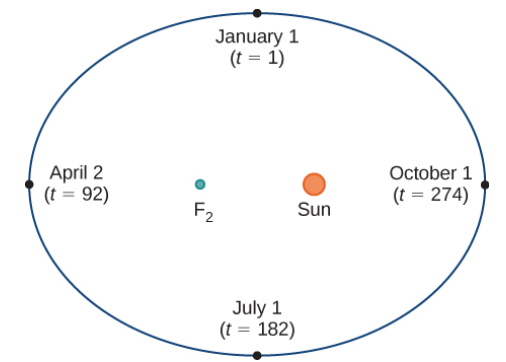
La Figura 8.1_1 representa la órbita de la Tierra alrededor del Sol durante un año. El punto etiquetado como F₂ es uno de los focos de la elipse; el otro foco está ocupado por el Sol. Si superponemos ejes de coordenadas sobre este gráfico, podemos asignar pares ordenados a cada punto de la elipse (Figura 8.1_2). Entonces, cada valor de x en el gráfico es un valor de posición en función del tiempo, y cada valor de y también es un valor de posición en función del tiempo. Por lo tanto, cada punto en la gráfica corresponde a un valor de la posición de la Tierra en función del tiempo.
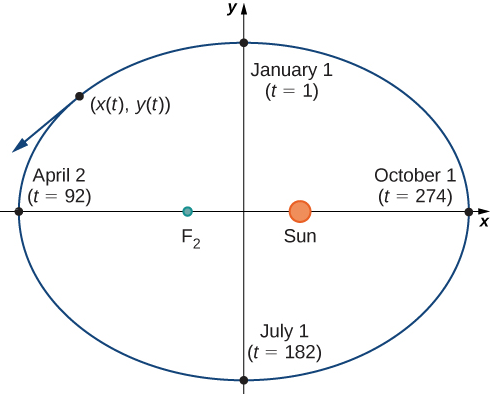
Podemos determinar las funciones para x(t) e y(t), parametrizando así la órbita de la Tierra alrededor del Sol. La variable t se llama parámetro independiente y, en este contexto, representa el tiempo relativo al comienzo de cada año.
Una curva en el plano (x, y) se puede representar paramétricamente. Las ecuaciones que se utilizan para definir la curva se denominan ecuaciones paramétricas.
DEFINICIÓN 8.1.1. ECUACIONES PARAMÉTRICAS
Si x e y son funciones continuas de t en un intervalo I, entonces las ecuaciones
x = x(t) e y = y(t)
se denominan ecuaciones paramétricas y t se llama parámetro. El conjunto de puntos (x, y) obtenidos a medida que t varía a lo largo del intervalo I se denomina gráfica de las ecuaciones paramétricas. La gráfica junto con las ecuaciones paramétricas se denomina asimismo curva paramétrica o curva plana, y se denota por C. ♦
Observe en esta definición que x e y se usan de dos maneras distintas. Primero como funciones de la variable independiente t. Como t varía durante el intervalo I, las funciones x(t) e y(t) generan un conjunto de pares ordenados (x, y). Este conjunto de pares ordenados genera la gráfica de las ecuaciones paramétricas. En este segundo uso, para designar los pares ordenados, x e y son variables. Es importante distinguir las variables x e y de las funciones x(t) e y(t).
EJEMPLO ILUSTRATIVO 8.1_1. Graficar una curva definida paramétricamente
Dibuje las curvas descritas por las siguientes ecuaciones paramétricas:
- x(t) = t − 1, y(t) = 2t + 4, −3 ≤ t ≤ 2
- x(t) = t² − 3, y(t) = 2t + 1, −2 ≤ t ≤ 3
- x(t) = 4 cost, y(t) = 4 sent, 0 ≤ t ≤ 2π
Solución:
a. x(t) = t − 1, y(t) = 2t + 4, −3 ≤ t ≤ 2
Para crear un gráfico de esta curva, primero configure una tabla de valores. Dado que la variable independiente tanto en x(t) como en y(t) es t, deje que t aparezca en la primera columna. Entonces, x(t) y y(t) aparecerán en la segunda y tercera columnas de la tabla.
| t | x(t) | y(t) |
|---|---|---|
| −3 | −4 | −2 |
| −2 | −3 | 0 |
| −1 | −2 | 2 |
| 0 | −1 | 4 |
| 1 | 0 | 6 |
| 2 | 1 | 8 |
La segunda y tercera columnas de esta tabla proporciona un conjunto de puntos que se trazarán. El gráfico de estos puntos aparece en la Figura 8.1_3. Las flechas del gráfico indican la orientación del gráfico, es decir, la dirección en la que se mueve un punto en el gráfico cuando t varía de −3 a 2.

b. x(t) = t² − 3, y(t) = 2t + 1, −2 ≤ t ≤ 3
Para crear una gráfica de esta curva, nuevamente configuramos una tabla de valores.
| t | x(t) | y(t) |
| -2 | 1 | −3 |
| -1 | −2 | −1 |
| 0 | −3 | 1 |
| 1 | −2 | 3 |
| 2 | 1 | 5 |
| 3 | 6 | 7 |
Las columnas segunda y tercera en esta tabla dan un conjunto de puntos para ser trazados (Figura 8.1_4). El primer punto en el gráfico (correspondiente a t = −2) tiene coordenadas (1, −3), y el último punto (correspondiente a t = 3) tiene coordenadas (6, 7). A medida que t progresa de −2 a 3, el punto en la curva viaja a lo largo de una parábola. La dirección en la que se mueve el punto se llama nuevamente orientación y se indica en la gráfica.
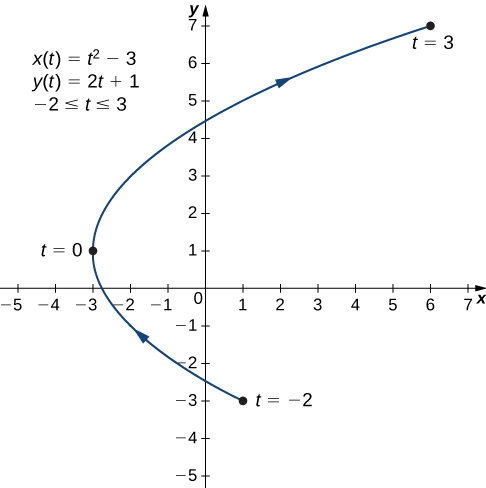
c. x(t) = 4cost, y(t) = 4sent, 0 ≤ t ≤ 2π
En este caso, usamos múltiplos de π/6 para t y creamos la siguiente tabla de valores:
| t | x(t) | y(t) |
| 0 | 4 | 0 |
| π/6 | 2√3 ≈ 3.5 | 2 |
| π/3 | 2 | 2√3 ≈ 3.5 |
| π/2 | 0 | 4 |
| 2π/3 | −2 | 2√3 ≈ 3.5 |
| 5π/6 | −2√3 ≈ −3.5 | 2 |
| π | −4 | 0 |
| 7π/6 | −2√3 ≈ −3.5 | 2 |
| 2π/3 | −2 | −2√3 ≈ −3.5 |
| 3π/2 | 0 | −4 |
| 5π/3 | 2 | −2√3 ≈ −3.5 |
| 11π/6 | 2√3 ≈ 3.5 | 2 |
| 2π | 4 | 0 |
La gráfica de esta curva plana aparece en el siguiente figura.

Esta es la gráfica de una circunferencia de radio 4 centrado en el origen, con una orientación hacia la izquierda. El punto inicial y los puntos finales de la curva tienen coordenadas (4, 0). ♦
Ejercicio de control 8.1_1
Dibuje la curva descrita por las ecuaciones paramétricas x(t) = 3t + 2, y(t) = t² − 1, −3 ≤ t ≤ 2. ♦
Eliminar el parámetro
Para comprender mejor la gráfica de una curva representada de manera paramétrica, es útil reescribir las dos ecuaciones como una sola ecuación que relaciona las variables x e y. Entonces podemos aplicar cualquier conocimiento previo de ecuaciones de curvas en el plano para identificar la curva. Por ejemplo, las ecuaciones que describen la curva plana del ejemplo 8.1_1b. son
x(t) = t² − 3, y(t) = 2t + 1, −2 ≤ t ≤ 3.
Resolver la segunda ecuación para t da
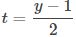
Lo anterior se puede sustituir en la primera ecuación:

Esta ecuación describe x como una función de y. Estos pasos dan un ejemplo de cómo eliminar el parámetro. La gráfica de esta función es una parábola que se abre a la derecha. Recuerde que la curva plana comienza en (1, −3) y termina en (6, 7). Estas terminaciones se debieron a la restricción del parámetro t.
EJEMPLO ILUSTRATIVO 8.1_2. Eliminar el parámetro
Elimine el parámetro para cada una de las curvas planas descritas por las siguientes ecuaciones paramétricas y describa el gráfico resultante.
a. x(t) = √(2t + 4), y(t) = 2t + 1, −2 ≤ t ≤ 6
b. x(t) = 4cost, y(t) = 3sent, 0 ≤ t ≤ 2π
Solución:
a. Para eliminar el parámetro, podemos resolver cualquiera de las ecuaciones para t. Por ejemplo, resolver la primera ecuación para t da
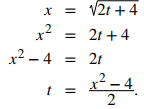
Tenga en cuenta que cuando cuadramos ambos lados, es importante observar que x ≥ 0. Sustituyendo t = (x² − 4)/2 en y(t) da como resultado

Se tiene la ecuación de una parábola que abre hacia arriba. Sin embargo, existe una restricción de dominio debido a los límites del parámetro t. Cuando t = −2, x = √[2(−2) + 4] = 0, y cuando t = 6, x = √[2(6) +4] = 4. A continuación se muestra la gráfica de esta curva plana.
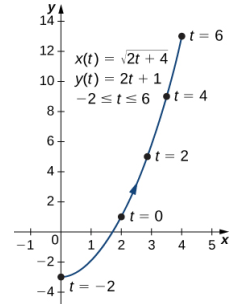
b. A veces es necesario ser un poco creativo para eliminar el parámetro. Las ecuaciones paramétricas de este ejemplo son
x(t) = 4cost e y(t) = 3sent.
No es aconsejable resolver ninguna de las ecuaciones para t directamente porque el seno y el coseno no son funciones uno a uno. Sin embargo, dividir la primera ecuación por 4 y la segunda ecuación por 3 (y suprimir la t) nos da
cost = x/4 y sent = y/3
Ahora use la identidad pitagórica cos²t + sen²t = 1 y reemplace las expresiones para sent y cost con las expresiones equivalentes en términos de x e y. Esto da

Ésta es la ecuación de una elipse horizontal centrada en el origen, con semieje mayor 4 y semieje menor 3 como se muestra en el siguiente gráfico.

A medida que t progresa de 0 a 2π, un punto de la curva recorre la elipse una vez, en sentido antihorario. Recuerde de la introducción a esta sección que la órbita de la Tierra alrededor del Sol también es elíptica. Este es un ejemplo perfecto del uso de curvas parametrizadas para modelar un fenómeno del mundo real. ♦
Ejercicio de control 8.1_2
Elimine el parámetro de la curva plana definida por las siguientes ecuaciones paramétricas y describa el gráfico resultante.
x(t) = 2 + 3t, y(t) = t − 1, 2 ≤ t ≤ 6. ♦
Hasta ahora hemos visto el método de eliminar el parámetro, asumiendo que conocemos un conjunto de ecuaciones paramétricas que describen una curva plana. ¿Qué pasa si quisiéramos comenzar con la ecuación de una curva y determinar un par de ecuaciones paramétricas para esa curva? Sin duda, esto es posible y, de hecho, es posible hacerlo de muchas formas diferentes para una curva determinada. El proceso se conoce como parametrización de una curva.
EJEMPLO ILUSTRATIVO 8.1_3. Parametrizar una curva
Encuentre dos pares diferentes de ecuaciones paramétricas para representar la gráfica de y = 2x² − 3.
Solución:
Primero, siempre es posible parametrizar una curva definiendo x(t) = t, luego reemplazando x con t en la ecuación para y(t). Esto da la parametrización
x(t) = t, y(t) = 2t² − 3.
Dado que no hay restricción en el dominio en el gráfico original, no hay restricción en los valores de t.
Tenemos total libertad en la elección de la segunda parametrización. Por ejemplo, podemos elegir
x(t) = 3t − 2. Lo único que tenemos que comprobar es que no se imponen restricciones a x; es decir, el rango de x(t) son todos números reales. Este es el caso de x(t) = 3t − 2. Ahora, como y = 2x² − 3, podemos sustituir x(t) = 3t − 2 por x. Se obtiene

Por tanto, una segunda parametrización de la curva se puede escribir como
x(t) = 3t − 2 y y(t) = 18t² − 24t + 6. ♦
Ejercicio de control 8.1_3
Encuentre dos conjuntos diferentes de ecuaciones paramétricas para representar la gráfica de y = x² + 2x. ♦
Cicloides y otras curvas paramétricas
Imagínese ir en bicicleta por el campo. Los neumáticos permanecen en contacto con la carretera y giran en un patrón predecible. Ahora supongamos que una hormiga muy decidida está cansada después de un largo día y quiere llegar a casa. Entonces se cuelga del costado de la llanta y obtiene un viaje gratis. El camino que recorre esta hormiga, yendo la bicicleta por un camino recto, se llama cicloide (Figura 8.1_8). Una cicloide generada por un círculo (o rueda de bicicleta) de radio a viene dada por las ecuaciones paramétricas
x(t) = a(t − sent), y(t) = a(1 − cost)
Para ver por qué esto es cierto, considere el camino que toma el centro de la rueda. El centro se mueve a lo largo del eje x a una altura constante igual al radio de la rueda. Si el radio es a, entonces las coordenadas del centro pueden estar dadas por las ecuaciones
x(t) = at, y(t) = a
para cualquier valor de t. A continuación, considere la hormiga, que gira alrededor del centro a lo largo de una trayectoria circular. Si la bicicleta se mueve de izquierda a derecha, las ruedas giran en el sentido de las agujas del reloj. Una posible parametrización del movimiento circular de la hormiga (relativo al centro de la rueda) viene dada por
x(t) = −asent, y(t) = −cost
(El signo negativo es necesario para invertir la orientación de la curva. Si el signo negativo no estuviera allí, tendríamos que imaginar la rueda girando en sentido antihorario). Al tomar estas ecuaciones juntas se obtienen las ecuaciones para la cicloide.
x(t) = a (t − sent), y(t) = a (1 − cost)

Figura 8.1_8 Una rueda que viaja por un camino sin patinar; el punto en el borde de la rueda traza una cicloide.
Ahora suponga que la rueda de la bicicleta no se desplaza por una carretera recta, sino que se desplaza por el interior de una rueda más grande, como en la figura 8.1_9. En este gráfico, el círculo verde se desplaza alrededor del círculo azul en dirección contraria a las agujas del reloj. Un punto en el borde del círculo verde traza el gráfico rojo, que se llama hipocicloide.

Las ecuaciones paramétricas generales para un hipocicloide son
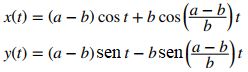
Estas ecuaciones son un poco más complicadas, pero su obtención es algo similar a las ecuaciones de la cicloide. En este caso asumimos que el radio del círculo más grande es a y que el radio del círculo más pequeño es b. Luego, el centro de la rueda se desplaza a lo largo de un círculo de radio a − b. Este hecho explica el primer término en cada ecuación anterior. El período de la segunda función trigonométrica en ambos x(t) y y(t) es igual a 2πb/(a − b).
La razón a/b está relacionada con el número de cúspides en el gráfico (las cúspides son las esquinas o extremos puntiagudos del gráfico), como se ilustra en la Figura 8.1_10. Esta relación puede dar lugar a unos gráficos muy interesantes, dependiendo de si la relación es racional o no. La figura 8.1_9 corresponde a a = 4 y b = 1. El resultado es un hipocicloide con cuatro cúspides. La figura 8.1_10 muestra algunas otras posibilidades. Los dos últimos hipocicloides tienen valores irracionales para a/b. En estos casos los hipocicloides tienen un número infinito de cúspides, por lo que nunca regresan a su punto de partida. Estos son ejemplos de lo que se conoce como curvas que llenan el espacio.


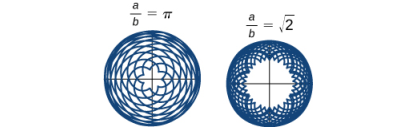

x=2cost,
y=8sint
Donde puedo encontrar las respuestas de los ejercicios propuesto por el cap 8.1 ECUACIONES PARAMÉTRICAS Y COORDENADAS POLARES
Buen trabajo, felicitaciones
Gracias. 👍
Exelente.
Excelente información
Gracias. Es con mucho gusto! 😺👀
Muy buena información y muchas gracias por su trabajo ha sido muy util.
∑Gracias por el comentario!∞