| 1. Funciones y sus gráficas |
1.3. Funciones trigonométricas: Objetivos de aprendizaje
1.3.1. Convertir medidas de ángulo entre grados y radianes.
1.3.2. Reconocer las definiciones triangulares y circulares de las funciones trigonométricas básicas.
1.3.3. Conocer las identidades trigonométricas básicas.
1.3.4. Identificar las gráficas y períodos de las funciones trigonométricas.
1.3.5. Describir el desplazamiento de un gráfico seno o coseno a partir de la ecuación de la función.
Las funciones trigonométricas se utilizan para modelar muchos fenómenos, incluidos las ondas de sonido, las vibraciones de las cuerdas, la corriente eléctrica alterna y el movimiento de los péndulos. De hecho, casi cualquier movimiento repetitivo o cíclico puede ser modelado por alguna combinación de funciones trigonométricas. En esta sección, definimos las seis funciones trigonométricas básicas y observamos algunas de las principales identidades que involucran estas funciones.
Medida de un ángulo en radianes
Para utilizar funciones trigonométricas, primero debemos entender cómo medir los ángulos. Aunque podemos usar radianes y grados, los radianes son una medida más natural porque están relacionados directamente con el círculo unitario, un círculo con radio 1.
La medida en radianes de un ángulo se define de la siguiente manera. Dado un ángulo θ, sea s la longitud del arco correspondiente en el círculo unitario (Figura 1.3_1). Decimos que el ángulo correspondiente al arco de longitud 1 tiene una medida de un radián.
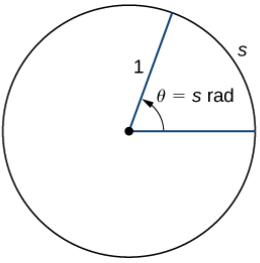
Dado que un ángulo de 360° corresponde a la circunferencia de un círculo, o un arco de longitud 2π, concluimos que un ángulo con una medida en grados de 360° tiene una medida en radianes de 2π. Del mismo modo, vemos que 180° es equivalente a π radianes. La tabla 1.3_1 muestra la relación entre el grado común (grado sexagesimal) y los valores en radianes.
| Grados | Radianes |
| 0 | 0 |
| 30 | π/6 |
| 45 | π/4 |
| 60 | π/3 |
| 90 | π/2 |
| 120 | 2π/3 |
| 135 | 3π/4 |
| 150 | 5π/6 |
| 180 | π |
Tabla 1.3_1 Ángulos comunes expresados en grados y radianes
Ejemplo ilustrativo 1.3_1 Conversión entre radianes y grados
a. Exprese 225° usando radianes.
b. Exprese 5π/3 rad usando grados.
Solución:
Use el hecho de que 180° es equivalente a π radianes como factor de conversión:
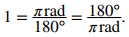
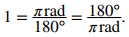
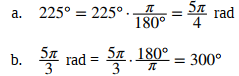
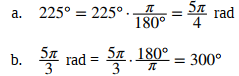
EJERCICIO DE CONTROL 1.3_1
Exprese 210 ° con radianes. Exprese 11π/6 rad en grados. ◊
Las seis funciones trigonométricas básicas
Las funciones trigonométricas nos permiten usar medidas de ángulos, en radianes o grados, para encontrar las coordenadas de un punto en cualquier círculo, no solo en un círculo unitario, o para encontrar un ángulo dado un punto en un círculo. También definen la relación entre los lados y los ángulos de un triángulo.
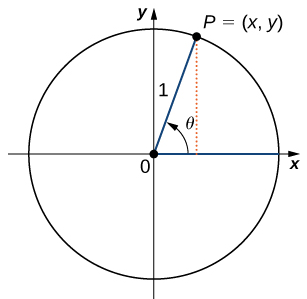
Para definir las funciones trigonométricas, primero consideremos el círculo unitario centrado en el origen y un punto P = (x, y) en el círculo unitario. Sea θ un ángulo con su lado inicial sobre el eje x positivo y con su lado terminal el segmento de recta OP. Se dice que el ángulo θ está en la posición estándar (Figura 1.3_2). Ahora podemos definir los valores de las seis funciones trigonométricas para θ en términos de las coordenadas x e y.

DEFINICIÓN Funciones trigonométricas
Sea P = (x, y) un punto en el círculo unitario centrado en el origen O. Sea θ un ángulo con su lado inicial a lo largo del eje x positivo y su lado terminal dado por el segmento de recta OP. Las seis funciones trigonométricas se definen como


Si x = 0, secθ y tanθ no están definidos. Si y = 0, entonces cotθ y cscθ no están definidos.
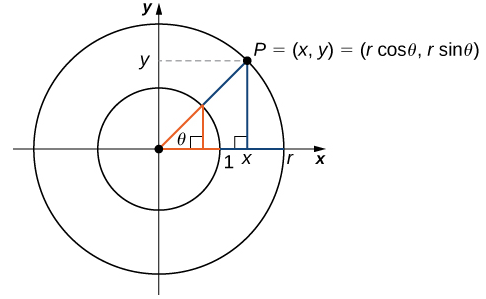
Podemos ver que para un punto P = (x, y) en un círculo de radio r con un ángulo correspondiente θ, las coordenadas x e y satisfacen


Los valores de las otras funciones trigonométricas también se pueden expresar en términos de x, y, y r (Figura 1.3_3).

La tabla 1.3_2 muestra los valores de seno y coseno en los ángulos principales en el primer cuadrante. A partir de esta tabla, podemos determinar los valores de seno y coseno en los ángulos correspondientes en los otros cuadrantes. Los valores de las otras funciones trigonométricas se calculan fácilmente a partir de los valores de senθ y cosθ.
| θ | senθ | cosθ |
| 0 | 0 | 1 |
| π/6 | 1/2 | √3/2 |
| π/4 | √2/2 | √2/2 |
| π/3 | √3/2 | 1/2 |
| π/2 | 1 | 0 |
Tabla 1.3_2 Valores de senθ y cosθ en ángulos θ en el primer cuadrante.
Ejemplo ilustrativo 1.3_2 Evaluación de funciones trigonométricas
Evalúa cada una de las siguientes expresiones.
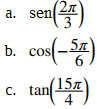
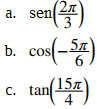
Solución:
a. En el círculo unitario, el ángulo θ = 2π/3 corresponde al punto (−1/2, √3/2). Por lo tanto, sen(2π/3) = y = √3/2.

b. Un ángulo θ = −5π/6 corresponde a una revolución en la dirección negativa, como se muestra. Por lo tanto, cos(−5π/6) = x = −3√/2.


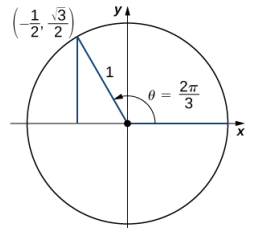
c. Un ángulo θ = 15π/4 = 2π + 7π/4. Por lo tanto, este ángulo corresponde a más de una revolución, como se muestra. Conociendo el hecho de que un ángulo de 7π/4 corresponde al punto (√2/2, −√2/2), podemos concluir que tan(15π/4) = y/x = −1.

EJERCICIO DE CONTROL 1.3_2
Evalúe cos(3π/4) y sen(−π/6). ◊
Las seis funciones trigonométricas como las razones de los lados de un triángulo rectángulo
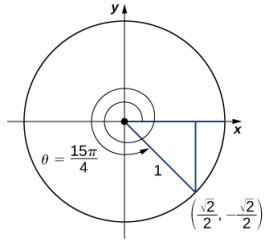
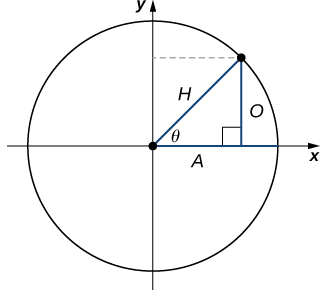
Como se mencionó anteriormente, las relaciones de las longitudes de los lados de un triángulo rectángulo se pueden expresar en términos de las funciones trigonométricas evaluadas en cualquiera de los ángulos agudos del triángulo. Sea θ uno de los ángulos agudos. Sea A la longitud del cateto adyacente al ángulo θ, sea O la longitud del cateto opuesto al ángulo θ y sea H la longitud de la hipotenusa. Al inscribir el triángulo en un círculo de radio H, como se muestra en la figura 1.3-4, vemos que A, H y O satisfacen las siguientes relaciones con el ángulo θ:



Ejemplo ilustrativo 1.3_3 Construyendo una rampa de madera
Se construirá una rampa de madera con un extremo en el suelo y el otro extremo en la parte superior de una escalera corta. Si la parte superior de la escalera está a 4 pies del suelo y el ángulo entre el suelo y la rampa debe ser de 10°, ¿qué longitud debe tener la rampa?
Solución:
Sea x la longitud de la rampa, en pies. En la siguiente imagen, vemos que x necesita satisfacer la ecuación sen(10°) = 4/x. Al resolver esta ecuación para x, vemos que x = 4/sen (10°) ≈ 23.035 pies.


EJERCICIO DE CONTROL 1.3_3
Un pintor de casas quiere apoyar una escalera de 20 pies contra una casa. Si el ángulo entre la base de la escalera y el suelo debe ser de 60°, ¿a qué distancia de la casa debe colocar la base de la escalera? ◊
Identidades trigonométricas
Una identidad trigonométrica es una ecuación que involucra funciones trigonométricas que es verdadera para todos los ángulos θ para los cuales se definen las funciones. Podemos usar las identidades para ayudarnos a resolver o simplificar ecuaciones. Las principales identidades trigonométricas se enumeran a continuación.
REGLA: IDENTIDADES TRIGONOMÉTRICAS
Identidades recíprocas
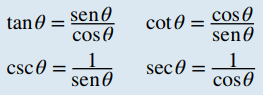
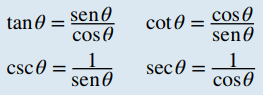
Identidades pitagóricas
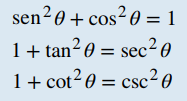
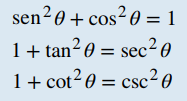
Fórmulas de suma y resta
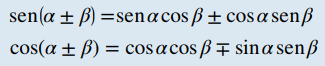
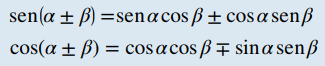
Fórmulas del ángulo doble
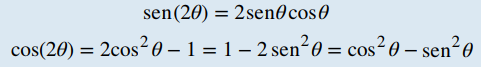
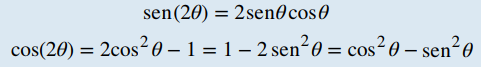
Ejemplo ilustrativo 1.3_4 Resolviendo Ecuaciones Trigonométricas
Para cada una de las siguientes ecuaciones, use una identidad trigonométrica para encontrar todas las soluciones.
a. 1 + cos(2θ) = cosθ
b. sen (2θ) = tanθ
Solución:
a. Usando la fórmula de doble ángulo para cos (2θ), vemos que θ es una solución de
1 + cos (2θ) = cosθ
si y sólo si
1 + 2cos²θ − 1 = cosθ,
lo cual es cierto si y sólo si
2cos²θ − cosθ = 0.
Para resolver esta ecuación, es importante tener en cuenta que necesitamos factorizar el lado izquierdo y no dividir ambos lados de la ecuación por cosθ. El problema con dividir por cosθ es que es posible que cosθ sea cero. De hecho, si dividieramos ambos lados de la ecuación por cosθ, perderíamos algunas de las soluciones de la ecuación original. Al factorizar el lado izquierdo de la ecuación, vemos que θ es una solución de esta ecuación si y sólo si
cosθ (2cosθ − 1) = 0.
Ya que cosθ = 0 cuando
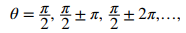
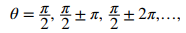
y cosθ = 1/2 cuando
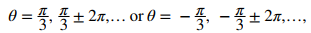
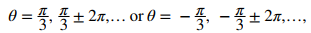
Concluimos que el conjunto de soluciones a esta ecuación es


y


Usando la fórmula de doble ángulo para sen(2θ) y la identidad recíproca para tan(θ), la ecuación se puede escribir como
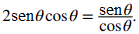
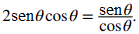
Para resolver esta ecuación, multiplicamos ambos lados por cosθ para eliminar el denominador, y observamos que si θ satisface esta ecuación, entonces θ satisface la ecuación
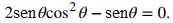
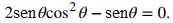
Sin embargo, debemos tener un poco de cuidado aquí. Incluso si θ satisface esta nueva ecuación, es posible que no satisfaga la ecuación original porque, para satisfacer la ecuación original, tendríamos que poder dividir ambos lados de la ecuación por cosθ. Sin embargo, si cosθ = 0, no podemos dividir ambos lados de la ecuación por cosθ. Por lo tanto, es posible que lleguemos a soluciones extrañas. Entonces, al final, es importante verificar las soluciones extrañas. Volviendo a la ecuación, es importante que factoricemos senθ de ambos términos en el lado izquierdo en lugar de dividir ambos lados de la ecuación por senθ. Factorizando el lado izquierdo de la ecuación, podemos reescribir esta ecuación como
senθ(2cos²θ − 1) = 0.
Por lo tanto, las soluciones están dadas por los ángulos θ de modo que senθ = 0 o cos2θ = 1/2. Las soluciones de la primera ecuación son θ = 0, ± π, ± 2π,…. Las soluciones de la segunda ecuación son θ = π/4, (π/4) ± (π/2), (π/4) ± π,…. Después de comprobar soluciones extrañas, el conjunto de soluciones para la ecuación es


EJERCICIO DE CONTROL 1.3_4
Encuentre todas las soluciones a la ecuación cos(2θ) = senθ. ◊
Ejemplo ilustrativo 1.3_5 Probar una identidad trigonométrica
Probar la identidad trigonométrica 1 + tan²θ = sec²θ.
Solución:
Comenzamos con la identidad.
sen²θ + cos²θ = 1.
Dividiendo ambos lados de esta ecuación por cos²θ, obtenemos
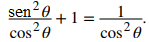
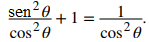
Como senθ/cosθ = tanθ y 1/cosθ = secθ, concluimos que
tan²θ + 1 = sec²θ. ◊
EJERCICIO DE CONTROL 1.3_5
Demuestre la identidad trigonométrica 1 + cot²θ = csc²θ. ◊
Gráficas y períodos de las funciones trigonométricas
Hemos visto que a medida que viajamos alrededor del círculo unitario, se repiten los valores de las funciones trigonométricas. Podemos ver este patrón en las gráficas de las funciones. Sea P = (x, y) un punto en el círculo unitario y sea θ el ángulo correspondiente. Dado que el ángulo θ y θ + 2π corresponden al mismo punto P, los valores de las funciones trigonométricas en θ y en θ + 2π son los mismos. En consecuencia, las funciones trigonométricas son funciones periódicas. El período de una función f se define como el valor positivo más pequeño p tal que f (x + p) = f (x) para todos los valores x en el dominio de f. Las funciones seno, coseno, secante y cosecante tienen un período de 2π. Dado que las funciones tangente y cotangente se repiten en un intervalo de longitud π, su período es π (Figura 1.3_5).


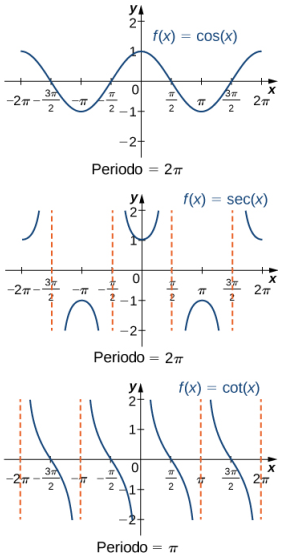

(Figura 1.3_5 Las seis funciones trigonométricas son periódicas.)
Al igual que con las funciones algebraicas, podemos aplicar transformaciones a las funciones trigonométricas. En particular, considere la siguiente función:
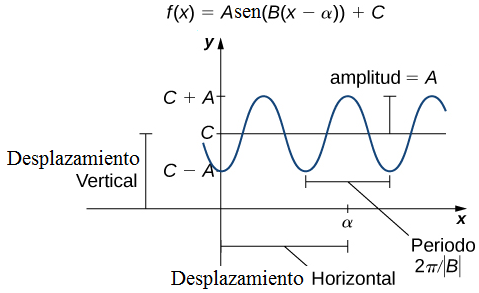
f (x) = Asen(B(x − α)) + C.
En la figura 1.3_6, la constante α provoca un desplazamiento horizontal o de fase. El factor B cambia el período. Esta función seno transformada tendrá un período 2π/|B|. El factor A da como resultado un estiramiento vertical por un factor de |A|. Decimos |A| es la “amplitud de f”. La constante C provoca un desplazamiento vertical.

Observe en la figura 1.3_5 que la gráfica de y = cosx es la gráfica de y = senx desplazada a la izquierda π/2 unidades. Por lo tanto, podemos escribir cosx = sen (x + π/2). De manera similar, podemos ver la gráfica de y = senx como la gráfica de y = cosx desplazada hacia la derecha π/2 unidades, y establecer que senx = cos(x − π/2).
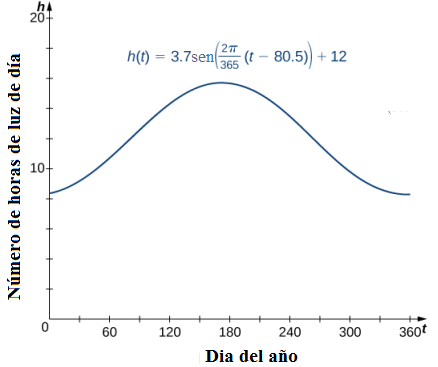
Una curva senoidal desplazada surge de forma natural al representar gráficamente el número de horas de luz de día en una ubicación determinada en función del día del año. Por ejemplo, suponga que una ciudad informa que el 21 de junio es el día más largo del año con 15.7 horas de luz de día y el 21 de diciembre es el día más corto del año con 8.3 horas de luz de día. Se puede demostrar que la función
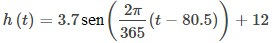
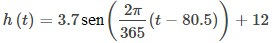
es un modelo para la cantidad de horas de luz del día h en función del día del año t (Figura 1.3_7).

Ejemplo ilustrativo 1.3_6 Dibujar la gráfica de una curva sinusoidal transformada
Dibuja la gráfica de f (x) = 3 sen(2(x − π/4)) + 1.
Solución:
Esta gráfica es un desplazamiento de fase de y = sen(x) a la derecha por π/4 unidades, seguido de una compresión horizontal por un factor de 2, un estiramiento vertical por un factor de 3, y luego un desplazamiento vertical por 1 unidad . El período de f es π.


EJERCICIO DE CONTROL 1.3_6
Describa la relación entre la gráfica de f (x) = 3sen(4x) −5 y la gráfica de y = sen(x). ◊
