| 7. Sucesiones y series infinitas | Ejercicios propuestos para el Capítulo 7.5 |
7.5 Series alternantes
Objetivos de aprendizaje:
7.5.1 Use la prueba de series alternantes para verificar la convergencia de una serie alternante.
7.5.2 Estime la suma de una serie alternante.
7.5.3 Explique el significado de convergencia absoluta y convergencia condicional.
Hasta ahora en este capítulo, hemos discutido principalmente series con términos positivos. En esta sección presentamos series alternantes, aquellas series cuyos términos se alternan en signos. En un capítulo posterior mostraremos que estas series a menudo surgen cuando se estudian las series de potencias. Después de definir series alternantes, presentamos la prueba de series alternantes para determinar si tal serie converge.
La prueba de la serie alternante
Una serie cuyos términos alternan entre valores positivos y negativos es una serie alternante. Por ejemplo, las series

y

son ambas series alternantes.
DEFINICIÓN 7.5_1. Serie alternante
Cualquier serie cuyos términos alternan entre valores positivos y negativos se denomina serie alternante. Se puede escribir una serie alternante en la forma
(1) \[ \sum_{n=1}^{\infty} (-1)^{n+1} \mathit{b}_{n} = \mathit{b}_{1} – \mathit{b}_{2} + \mathit{b}_{3} – \mathit{b}_{4} + \cdots \]
(2) \[ \sum_{n=1}^{\infty} (-1)^{n} \mathit{b}_{n} = -\mathit{b}_{1} + \mathit{b}_{2} – \mathit{b}_{3} + \mathit{b}_{4} – \cdots \]
Donde bn ≥ 0 para todos los enteros positivos n. ♦
◊ La serie

es una serie geométrica. Como |r| = |−1/2| < 1, la serie converge.
◊ La serie

se denomina serie armónica alternante. Mostraremos que mientras la serie armónica diverge, la serie armónica alternante converge.
Para probar esto, observamos la secuencia de sumas parciales {Sk} (Vea la figura 7.5_1).
Prueba:
Considere los términos impares S2k + 1 para k ≥ 0. Como 1/(2k + 1) < 1 / 2k,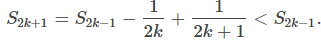 Por lo tanto, {S2k + 1} es una secuencia decreciente. También,
Por lo tanto, {S2k + 1} es una secuencia decreciente. También,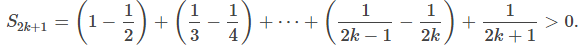 Por lo tanto, {S2k + 1} está acotada inferiormente. Dado que {S2k + 1} es una secuencia decreciente que está acotada inferiormente, por el Teorema de convergencia monótona, {S2k + 1} converge. Del mismo modo, los términos pares {S2k} forman una secuencia creciente que está acotada superiormente porque
Por lo tanto, {S2k + 1} está acotada inferiormente. Dado que {S2k + 1} es una secuencia decreciente que está acotada inferiormente, por el Teorema de convergencia monótona, {S2k + 1} converge. Del mismo modo, los términos pares {S2k} forman una secuencia creciente que está acotada superiormente porque y
y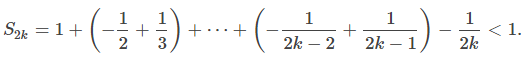 Por lo tanto, según el Teorema de convergencia monótona, la secuencia {S2k} también converge. Como
Por lo tanto, según el Teorema de convergencia monótona, la secuencia {S2k} también converge. Como
entonces Sea S = limk → ∞ S2k + 1 y usando el hecho de que 1/(2k + 1) → 0, concluimos que limk → ∞ S2k = S. Dado que los términos impares y los términos pares en la secuencia de sumas parciales convergen al mismo límite S, se deduce que la secuencia de sumas parciales converge a S, y por lo tanto la serie armónica alterna converge a S.
Sea S = limk → ∞ S2k + 1 y usando el hecho de que 1/(2k + 1) → 0, concluimos que limk → ∞ S2k = S. Dado que los términos impares y los términos pares en la secuencia de sumas parciales convergen al mismo límite S, se deduce que la secuencia de sumas parciales converge a S, y por lo tanto la serie armónica alterna converge a S.
También se puede mostrar que S = ln2, y podemos escribir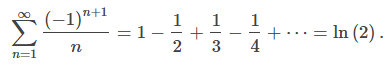
 (Figura 7.5_1. Para las series armónicas alternantes, los términos impares S2k + 1 en la secuencia de sumas parciales están decreciendo y acotados por abajo. Los términos pares S2k están creciendo y acotados por arriba.)
(Figura 7.5_1. Para las series armónicas alternantes, los términos impares S2k + 1 en la secuencia de sumas parciales están decreciendo y acotados por abajo. Los términos pares S2k están creciendo y acotados por arriba.)
♦
Más generalmente, cualquier serie alternante de la forma (1) o de la forma (2) (Ecuación 5.14) converge siempre que b1 ≥ b2 ≥ b3 ≥ ⋯ y bn→0 (Figura 7.5_2). La demostración es similar a la de la serie armónica alternante.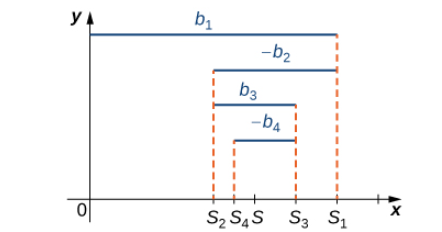
(Figura 7.5_2. Para una serie alternante b1−b2+b3−⋯ donde b1− b2 − b3 − … en que b1 > b2 > b3 > …, los términos impares S2k + 1 en la sucesión de sumas parciales son decrecientes y acotados inferiormente. Los términos pares S2k son crecientes y acotados superiormente.)
TEOREMA 7.5_1. Prueba de la serie alternante
Una serie alternante de la forma:
\[\sum_{n=1}^{\infty}(-1)^{n+1}b_{n} \quad \text{o} \quad \sum_{n=1}^{\infty}(-1)^{n}b_{n}\]converge si
i. 0 ≤ bn + 1 ≤ bn para todos los n ≥ 1 y
ii. limn → ∞ bn = 0.
Esto se conoce como la prueba de series alternantes. ♦
Observamos que este teorema es cierto de manera más general siempre que exista algún número entero N tal que 0 ≤ bn + 1 ≤ bn para todos los n ≥ N.
EJEMPLO ILUSTRATIVO 7.5_1. Convergencia de series alternantes
Para cada una de las siguientes series alternantes, determine si la serie converge o diverge.
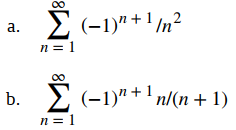
Solución:
a. Ya que

la serie converge.
b. Dado que \(n/(n + 1) \to 0\) cuando \(n \to \infty\), no podemos aplicar la prueba de la serie alternante. En cambio, usamos la prueba del n-ésimo término para la divergencia. Dado que
\[\lim_{n\to\infty} \frac{(-1)^{n+1}n}{n+1} \ne 0,\]
la serie diverge.
♦
Ejercicio de control 7.5.1
Determine si la serie \(\sum_{n=1}^{\infty} \frac{(-1)^{n+1}n}{2^n}\) converge o diverge.
♦
Resto de una serie alternante
Es difícil calcular explícitamente la suma de la mayoría de las series alternantes, por lo que típicamente la suma se aproxima utilizando una suma parcial. Al hacerlo, estamos interesados en la magnitud del error en nuestra aproximación. Considere una serie alternante

que satisface las hipótesis de la prueba de series alternantes. Supongamos que S denota la suma de esta serie y {Sk} es la secuencia correspondiente de sumas parciales. De la figura 7.5_2, vemos que para cualquier número entero N ≥ 1, el resto RN satisface

TEOREMA 7.5_2. Restos en series alternantes
Considere una serie alternante de la forma
\[\sum_{n=1}^{\infty}(-1)^{n+1}b_{n} \quad \text{o} \quad \sum_{n=1}^{\infty}(-1)^{n}b_{n}\]que satisface las hipótesis de la prueba de series alternantes. Supongamos que S denota la suma de la serie y SN denota la enésima suma parcial. Para cualquier número entero N ≥ 1, el resto RN = S − SN satisface
\[|R_{N}| \leq b_{N+1}.\]♦
En otras palabras, si se aplican las condiciones de la prueba de series alternantes, entonces el error al aproximar las series infinitas por la enésima suma parcial SN es en magnitud como máximo del tamaño del siguiente término bN + 1.
EJEMPLO ILUSTRATIVO 7.5_2. Estimando el resto de una serie alternante
Considere la serie alternante

Use la fórmula para la estimación del resto de una serie alternante para determinar un margen de error R10 si aproximamos la suma de la serie por la suma parcial S10.
Solución:
Del teorema indicado anteriormente,

♦
Ejercicio de control 7.5.2
Encuentra una cota para \(R_{20}\) al aproximar la serie \(\sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n}\) mediante \(S_{20}\). ♦Convergencia absoluta y condicional
Considere una serie infinita
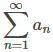
y la serie relacionada

Aquí discutimos las posibilidades para la relación entre la convergencia de estas dos series. Por ejemplo, considere la serie armónica alternante

La serie cuyos términos son el valor absoluto de estos términos es la serie armónica, ya que

Dado que la serie armónica alternante converge, pero la serie armónica diverge, decimos que la serie armónica alternante exhibe convergencia condicional.
En comparación, considere la serie

La serie cuyos términos son los valores absolutos de los términos de esta serie es la serie

Dado que ambas series convergen, decimos que la serie

exhibe convergencia absoluta.
DEFINICIÓN 7.5_1. Convergencia absoluta y convergencia condicional
Una serie \(\sum_{n=1}^{\infty} a_n\) exhibe convergencia absoluta si \(\sum_{n=1}^{\infty} |a_n|\) converge.
Una serie \(\sum_{n=1}^{\infty} a_n\) exhibe convergencia condicional si \(\sum_{n=1}^{\infty} a_n\) converge pero \(\sum_{n=1}^{\infty} |a_n|\) diverge.
♦
Como se muestra en la serie armónica alternante, una serie
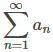
puede converger, pero

puede divergir. En el siguiente teorema, sin embargo, mostramos que si

converge, entonces
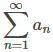
converge.
TEOREMA 7.5_3. La convergencia absoluta implica convergencia
Si \[ \sum_{n=1}^{\infty} |a_n| \text{ converge, entonces } \sum_{n=1}^{\infty} a_n \text{ converge.} \]
♦
Prueba:
Suponga que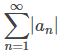 converge. Mostramos esto usando el hecho de que an = |an| o an = −|an| y por lo tanto |an| + an = 2|an| o |an| + an = 0. Por lo tanto, 0 ≤ |an| + an ≤ 2|an|. En consecuencia, por la prueba de comparación, ya que
converge. Mostramos esto usando el hecho de que an = |an| o an = −|an| y por lo tanto |an| + an = 2|an| o |an| + an = 0. Por lo tanto, 0 ≤ |an| + an ≤ 2|an|. En consecuencia, por la prueba de comparación, ya que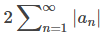 converge, la serie
converge, la serie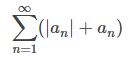 converge. Al usar las propiedades algebraicas para series convergentes, concluimos que
converge. Al usar las propiedades algebraicas para series convergentes, concluimos que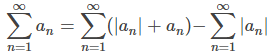 converge. ♦
converge. ♦
EJEMPLO ILUSTRATIVO 7.5_3. Convergencia absoluta versus convergencia condicional
Para cada una de las siguientes series, determine si la serie converge absolutamente, converge condicionalmente o diverge.

Solución:
a. Podemos ver que

diverge utilizando la prueba de comparación de límites con la serie armónica. De hecho,

Por lo tanto, la serie no converge absolutamente. Sin embargo, dado que

la serie converge. Podemos concluir que

converge condicionalmente.
b. Observando que |cosn| ≤ 1, para determinar si la serie converge absolutamente, compare

con la serie

Ya que

converge, por la prueba de comparación,

converge, y por lo tanto

converge absolutamente. ♦
Ejercicio de control 7.5.3
Determine si la serie \( \sum_{n=1}^{\infty} \frac{(-1)^{n+1} n}{2n^3 + 1} \) converge absolutamente, converge condicionalmente o diverge. ♦
Para ver la diferencia entre la convergencia absoluta y la condicional, observe lo que sucede cuando reorganizamos los términos de la serie armónica alternante

Mostramos que podemos reorganizar los términos para que la nueva serie diverja. Ciertamente, si reorganizamos los términos de una suma finita, la suma no cambia. Sin embargo, cuando trabajamos con una suma infinita, pueden suceder cosas interesantes.
Empezamos agregando suficientes términos positivos para producir una suma que sea mayor que un número real M > 0. Por ejemplo, sea M = 10 y hallemos un número entero k tal que

(Podemos hacer esto porque la serie \( \sum_{n=1}^{\infty} \frac{1}{2n-1} \) diverge a infinito). Luego restamos 1/2. Después añadimos más términos positivos hasta que la suma alcance 100. Es decir, encontramos otro entero \(j > k\) tal que
\( 1 + \frac{1}{3} + \dots + \frac{1}{2k-1} – \frac{1}{2} + \frac{1}{2k+1} + \dots + \frac{1}{2j+1} > 100. \)
Luego restamos 1/4. Continuando de esta manera, hemos encontrado una manera de reorganizar los términos en la serie armónica alternante de modo que la secuencia de sumas parciales para la serie reorganizada sea no acotada y, por lo tanto, diverja.
Los términos en la serie armónica alternante también se pueden reorganizar para que la nueva serie converja a un valor diferente. En el ejemplo 7.5_4, mostraremos cómo reorganizar los términos para crear una nueva serie que converja a 3ln(2)/2. Señalamos que las series armónicas alternantes se pueden reorganizar para crear una serie que converja a cualquier número real r; sin embargo, la prueba de ese hecho está más allá del alcance de este texto.
En general, cualquier serie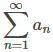 que converge condicionalmente puede reorganizarse para que la nueva serie diverja o converja a un número real diferente. Una serie que converge absolutamente no tiene esta propiedad. Para cualquier serie
que converge condicionalmente puede reorganizarse para que la nueva serie diverja o converja a un número real diferente. Una serie que converge absolutamente no tiene esta propiedad. Para cualquier serie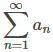 que converge absolutamente, el valor de
que converge absolutamente, el valor de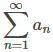 es el mismo para cualquier reordenamiento de los términos. Este resultado se conoce como el Teorema de reordenamiento de Riemann, que está más allá del alcance de estas primeras lecciones introductorias.
es el mismo para cualquier reordenamiento de los términos. Este resultado se conoce como el Teorema de reordenamiento de Riemann, que está más allá del alcance de estas primeras lecciones introductorias.
EJEMPLO ILUSTRATIVO 7.5_4. Reordenando series
Usa el hecho de que

para reorganizar los términos en la serie armónica alternante para que la suma de las serie reordenada sea 3ln(2)/2.
Solución:
Sea

Ya que

por las propiedades algebraicas de series convergentes,

Ahora introduzca la serie

tal que para todos n ≥ 1, b2n − 1 = 0 y b2n = an/2. Entonces

Luego, utilizando las propiedades algebraicas del límite de las series convergentes,, dado que

convergen, la serie

converge y
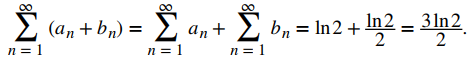
Ahora agregando los términos correspondientes, an y bn, vemos que
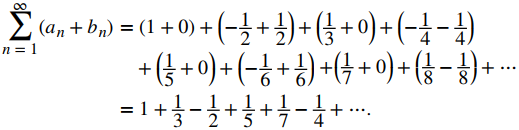
Notamos que la serie en el lado derecho del signo igual es un reordenamiento de la serie armónica alternante. Ya que

concluimos que

Por lo tanto, hemos encontrado una reorganización de la serie armónica alternante que tiene la propiedad deseada. ♦

Muy bueno
Gracias por el comentario ∑
Buena forma de explicar, y buena publicación para obtener información sobre mi tema de presentación, que voy a exponer en la universidad. Gracias!