| 9. Ecuaciones diferenciales | 

9.5 Ecuaciones lineales de segundo orden: Objetivos de aprendizaje

    En este CAPÍTULO 9.5 estudiamos una clase particularmente importante de ecuaciones de segundo orden. Debido a sus muchas aplicaciones en ciencias e ingeniería, las ecuaciones diferenciales de segundo orden han sido históricamente la clase de ecuaciones diferenciales más estudiada. La investigación sobre la teoría de ecuaciones diferenciales de segundo orden continúa hasta nuestros días. Este capítulo está dedicado a ecuaciones de segundo orden que se pueden escribir en la forma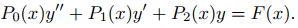Se dice que estas ecuaciones son lineales. Como en el caso de las ecuaciones lineales de primer orden, se dice que la ED lineal de segundo orden es homogénea si F ≡ 0, o no homogénea si F no es idénticamente 0.

La SECCIÓN 9.5.1 está dedicada a la teoría de ecuaciones lineales homogéneas de segundo orden.

La SECCIÓN 9.5.2 trata de ecuaciones lineales homogéneas de la forma especialdonde a, b y c son constantes (a ≠ 0). Cuando haya completado esta sección, sabrá todo lo que hay que saber sobre cómo resolver estas ecuaciones.

La SECCIÓN 9.5.3 presenta la teoría de ecuaciones lineales no homogéneas de segundo orden.

Las SECCIONES 9.5.4 y 9.5.5 presentan el método de coeficientes indeterminados, que se puede utilizar para resolver ecuaciones lineales no homogéneas de la forma

donde a, b y c son constantes y F tiene una forma especial que todavía es lo suficientemente general como para ocurrir en muchas aplicaciones. En esta sección hacemos un amplio uso de la idea de variación de parámetros presentada en el Capítulo 9.2.

La SECCIÓN 9.5.6 trata de la reducción de orden, una técnica basada en la idea de variación de parámetros, que nos permite encontrar la solución general de una ecuación lineal de segundo orden no homogénea siempre que conozcamos una solución no trivial (no idénticamente cero) de la ecuación homogénea asociada. 

La SECCIÓN 9.5.7 trata del método tradicionalmente llamado variación de parámetros, que nos permite encontrar la solución general de una ecuación lineal de segundo orden no homogénea siempre que conozcamos dos soluciones no triviales (con razón no constante) de la ecuación homogénea asociada.

9.5.1 ECUACIONES LINEALES HOMOGÉNEAS

Se dice que una ecuación diferencial de segundo orden es lineal si se puede escribir como

y″ + p(x)y′ + q(x)y = f (x).                     (9.5.1.1)

Llamamos a la función f de la derecha una función de forzamiento, ya que en aplicaciones físicas a menudo está relacionada con una fuerza que actúa sobre algún sistema modelado por la ecuación diferencial. Decimos que (9.5.1.1) es homogénea si f ≡ 0 o no homogénea si f no es idénticamente 0. Dado que estas definiciones son como las definiciones correspondientes de la Sección 9.2.1 para la ecuación lineal de primer orden

y′ + p(x)y = f (x),                    (9.5.1.2)

es natural esperar similitudes entre los métodos de resolución de (9.5.1.1) y (9.5.1.2). Sin embargo, resolver (9.5.1.1) es más difícil que resolver (9.5.1.2). Por ejemplo, mientras que el Teorema 9.2.1.1 da una fórmula para hallar la solución general de (9.5.1.2) en el caso donde f ≡ 0 y el Teorema 9.2.1.2 da una fórmula para el caso donde f no es idénticamente 0, no hay fórmulas para hallar la solución general de (9.5.1.1) en cualquier caso. Por lo tanto, debemos contentarnos con resolver ecuaciones lineales de segundo orden de formas especiales.

En la Sección 9.2.1, primero consideramos la ecuación homogénea y′ + p(x)y = 0, y luego usamos una solución no trivial de esta ecuación para encontrar la solución general de la ecuación no homogénea y′ + p(x)y = f (x). Aunque la progresión del caso homogéneo al no homogéneo no es tan simple para la ecuación lineal de segundo orden, todavía es necesario resolver la ecuación homogénea

y″ + p(x)y′ + q(x)y = 0                     (9.5.1.3)

para resolver la ecuación no homogénea (9.5.1.1). Esta sección está dedicada a (9.5.1.3).

   

       El siguiente teorema proporciona condiciones suficientes para la existencia y unicidad de las soluciones de problemas de valor inicial para (9.5.1.3). Omitimos la prueba.

Teorema 9.5.1.1

Supongamos que p y q son continuas en un intervalo abierto (a, b), sea x₀ cualquier punto en (a, b) y sean k₀ y k₁ números reales arbitrarios. Entonces el problema de valor inicial

tiene una solución única en (a, b). ♦

Como y ≡ 0 es obviamente una solución de (9.5.1.3), la llamamos solución trivial. Cualquier otra solución es no trivial. Bajo los supuestos del teorema 9.5.1.1, la única solución del problema de valor inicial

en (a, b) es la solución trivial (Ejercicio 9.5.24).

    Los siguientes tres ejemplos ilustran conceptos que desarrollaremos más adelante en esta sección. No debería preocuparse por cómo encontrar las soluciones dadas de las ecuaciones en estos ejemplos. Esto se explicará en secciones posteriores.

Ejemplo ilustrativo 9.5.1_1

Los coeficientes de y′ y y en

y″ − y = 0                     (9.5.1.4)

son las funciones constantes p ≡ 0  y  q ≡ −1, que son continuas en (−∞, ∞). Por lo tanto, el Teorema 9.5.1.1 implica que todo problema de valor inicial para (9.5.1.4) tiene una solución única en (−∞, ∞).

(a) Verifique que y₁ = eˣ  y  y₂ = e⁻ˣ son soluciones de (9.5.1.4) en (−∞, ∞).
(b) Verifique que si c₁ y c₂ son constantes arbitrarias, y = c₁eˣ + c₂e⁻ˣ es una solución de (9.5.1.4) en (−∞, ∞).
(c) Resuelva el problema de valor inicial

       (9.5.1.5)

Solución:

(a) Si y₁ = eˣ entonces y₁′ = eˣ  y  y₁″ = eˣ = y₁, entonces y₁″ − y₁ = 0. Si y₂ = e⁻ˣ, entonces y₂′ = −e⁻ˣ  y  y₂″ = e⁻ˣ = y₂, entonces y₂″ − y₂ = 0.

(b) Si

y = c₁eˣ + c₂e⁻ˣ                  (9.5.1.6)

entonces

y′ = c₁eˣ − c₂e⁻ˣ                  (9.5.1.7)

y

y″ = c₁eˣ + c₂e⁻ˣ

entonces

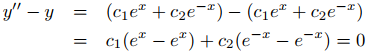
para todo x. Por lo tanto y = c₁eˣ + c₂e⁻ˣ es una solución de (9.5.1.4) en (−∞, ∞).

(c) Podemos resolver el problema de valor inicial (9.5.1.5) eligiendo c₁ y c₂ en (9.5.1.6) de modo que y(0) = 1 e y′(0) = 3. Estableciendo x = 0 en (9.5.1.6) y (9.5.1.7 ) muestra que esto es equivalente a

Resolver estas ecuaciones produce c₁ = 2 y c₂ = −1. Por lo tanto y = 2eˣ − e⁻ˣ  es la única solución de (9.5.1.5) en (−∞, ∞).  ♦

Ejemplo ilustrativo 9.5.1_2

Sea ω una constante positiva. Los coeficientes de y′  y  y en

y″ + ω²y = 0              (9.5.1.8)

son las funciones constantes p ≡ 0 y q ≡ ω², que son continuas en (−∞, ∞). Por lo tanto, el teorema 9.5.1.1 implica que todo problema de valor inicial para (9.5.1.8) tiene una solución única en (−∞, ∞).

(a) Verifique que y₁ = cosωx  y  y₂ = senωx son soluciones de (9.5.1.8) en (−∞, ∞).
(b) Verifique que si c₁ y c₂ son constantes arbitrarias, entonces y = c₁cosωx + c₂senωx es una solución de (9.5.1.8) en (−∞, ∞).
(c) Resuelva el problema de valor inicial

y″ + ω²y = 0,   y(0) = 1, y′(0) = 3       (9.5.1.9)

Solución:

(a)  Si y₁ = cosωx, entonces  y₁′ = −ωsenωx  y  y₁″ = −ω²cosωx = −ω²y₁, entonces  y₁″ + ω²y₁ = 0.

Si y₂ = senωx, entonces  y₂′ = ωcosωx  y  y₂″ = −ω²senωx = −ω²y₂, entonces  y₂″ + ω²y₂ = 0.

(b)  Si      

              (9.5.1.10)

entonces

              (9.5.1.11)

y

de tal modo que

para todo x. Por lo tanto y = c₁ cosωx + c₂senωx es una solución de (9.5.1.8) en (−∞, ∞).

(c)  Para resolver (9.5.1.9), debemos elegir c₁ y c₂ en (9.5.1.10) de modo que y(0) = 1  e  y′(0) = 3. Estableciendo x = 0 en (9.5.1.10) y (9.5. 1.11) muestra que c₁ = 1  y  c₂ = 3/ω. Por lo tanto

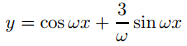
es la única solución de (9.5.1.9) en (−∞, ∞).  ♦

       El teorema 9.5.1.1 implica que si k₀ y k₁ son números reales arbitrarios, entonces el problema de valor inicial

        (9.5.1.12)

tiene una solución única en un intervalo (a, b) que contiene x₀, siempre que P₀, P₁ y P₂ sean continuos y P₀ no tenga ceros en (a, b). Para ver esto, reescribimos la ecuación diferencial en (9.5.1.12) como

y aplique el teorema 9.5.1.1 con p = P₁/P₀  y  q = P₂ /P₀.

Ejemplo ilustrativo 9.5.1_3

La ecuación

              (9.5.1.13)

tiene la forma de la ecuación diferencial en (9.5.1.12), con P₀(x) = x², P₁(x) = x, y P₂(x) = −4, que son todas continuas en (−∞, ∞) . Sin embargo, dado que P₀(0) = 0 debemos considerar las soluciones de (9.5.1.13) en (−∞, 0) y (0, ∞). Dado que P₀ no tiene ceros en estos intervalos, el teorema 9.5.1.1 implica que el problema de valor inicial

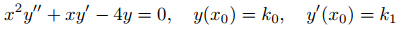
tiene una solución única en (0, ∞) si x₀ > 0, o en (−∞, 0)  si  x₀ < 0.

(a)  Verifique que y₁ = x² es una solución de (9.5.1.13) en (−∞, ∞)  y  y₂ = 1/x² es una solución de (9.5.1.13) en (−∞, 0) y (0, ∞).
(b)  Verifique que si  c₁  y  c₂ son constantes cualesquiera, entonces y = c₁x² + c₂/x² es una solución de (9.5.1.13) en (−∞, 0) y (0, ∞).
(c)  Resuelva el problema de valor inicial

      (9.5.1.14)

(d)  Resuelva el problema de valor inicial

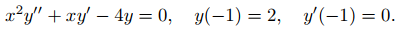      (9.5.1.15)

Solución:

(a)  Si y₁ = x², entonces y₁′ = 2x  y  y₁″= 2, de tal modo que

para todo x en (−∞, ∞).

Si y₂ = 1/x², entonces y₂′ = −2/x³  y  y₂″ = 6/x⁴, de tal modo que

para x en (−∞, 0) o (0, ∞).

(b)  Si

              (9.5.1.16)

entonces

              (9.5.1.17)

y

de tal modo que

para x en (−∞, 0) o (0, ∞).

(c)  Para resolver (9.5.1.14), elegimos c₁ y c₂ en (9.5.1.16) de modo que y(1) = 2 e y′(1) = 0. Estableciendo x = 1 en (9.5.1.16) y (9.5.1.17) muestra que esto es equivalente a

Resolver estas ecuaciones produce c₁ = 1 y c₂ = 1. Por lo tanto, y = x² + 1/x² es la única solución de (9.5.1.14) en (0, ∞).

(d)  Podemos resolver (9.5.1.15) eligiendo c₁ y c₂ en (9.5.1.16) de modo que y(−1) = 2  y  y′ (−1) = 0. Establecer x = −1 en (9.5.1.16) y (9.5.1.17) muestra que esto es equivalente a

Resolver estas ecuaciones produce c₁ = 1 y c₂ = 1. Por lo tanto, y = x² + 1/x² es la única solución de (9.5.1.15) en (−∞, 0). ♦

        Aunque las fórmulas para las soluciones de (9.5.1.14) y (9.5.1.15) son ambas y = x² + 1/x², no debe concluir que estos dos problemas de valores iniciales tienen la misma solución. Recuerde que la solución de un problema de valor inicial se define en un intervalo que contiene el punto inicial; por lo tanto, la solución de (9.5.1.14) es y = x² + 1/x² en el intervalo (0, ∞), que contiene el punto inicial x₀ = 1, mientras que la solución de (9.5.1.15) es y = x² + 1/x² en el intervalo (−∞, 0), que contiene el punto inicial x₀ = −1.

La solución general de una ecuación lineal homogénea de segundo orden

Si y₁ e y₂ se definen en un intervalo (a, b) y c₁ y c₂ son constantes, entonces

es una combinación lineal de y₁ e y₂. Por ejemplo, y = 2cosx + 7senx es una combinación lineal de y₁ = cosx y y₂ = senx, con c₁ = 2 y c₂ = 7.

El siguiente teorema establece un hecho que ya hemos verificado en los ejemplos 9.5.1.1, 9.5.1.2 y 9.5.1.3.

Teorema 9.5.1.2

Si y₁ y y₂ son soluciones de la ecuación homogénea

              (9.1.5.18)

en (a, b), entonces cualquier combinación lineal

            (9.1.5.19)

de y₁ y y₂ también es una solución de (9.5.1.18) en (a, b).  ♦

Prueba: Si entonces y Por lo tanto ya que y1 y y2 son soluciones de (9.5.1.18). ◊

       Decimos que {y₁, y₂} es un conjunto fundamental de soluciones de (9.5.1.18) en (a, b) si cada solución de (9.5.1.18) en (a, b) se puede escribir como una combinación lineal de y₁ y y₂ como en (9.5.1.19). En este caso decimos que (9.5.1.19) es la solución general de (9.5.1.18) en (a, b).

Independencia lineal

Necesitamos una forma de determinar si un conjunto dado {y₁, y₂} de soluciones de (9.5.1.18) es un conjunto fundamental. La siguiente definición nos permitirá enunciar las condiciones necesarias y suficientes para ello.

      Decimos que dos funciones y₁ e y₂ definidas en un intervalo (a, b) son linealmente independientes en (a, b) si ninguna es múltiplo constante de la otra en (a, b). (En particular, esto significa que ninguna puede ser la solución trivial de (9.5.1.18), ya que, por ejemplo, si y₁ ≡ 0 podríamos escribir y₁ = 0·y₂.) También diremos que el conjunto {y₁, y₂} es linealmente independiente en (a, b).

Teorema 9.5.1.3

Suponga que p y q son continuas en (a, b). Entonces un conjunto {y₁, y₂} de soluciones de

y″ + p(x)y′ + q(x)y = 0        (9.5.1.20)

en (a, b) es un conjunto fundamental si y solo si {y₁, y₂} es linealmente independiente en (a, b). ♦

       Presentaremos la demostración del Teorema 9.5.1.3 en pasos que vale la pena considerar como teoremas por derecho propio. Sin embargo, primero interpretemos el teorema 9.5.1.3 en términos de los ejemplos 9.5.1.1, 9.5.1.2 y 9.5.1.3.

Ejemplo ilustrativo 9.5.1_4

(a) Dado que e^x/e^−x = e^2x no es constante, el teorema 9.5.1.3 implica que y = c₁e^x + c₂e^−x es la solución general de y″ − y = 0 en (−∞, ∞).
(b) Como cosωx / senωx = cotωx no es constante, el teorema 9.5.1.3 implica que y = c₁cosωx + 2senωx es la solución general de y″ + ω²y = 0 en (−∞, ∞).
(c) Dado que x²/x⁻² = x⁴ no es constante, el teorema 9.5.1.3 implica que y = c₁x² + c₂/x² es la solución general de x²y″ + xy′ − 4y = 0 en (−∞, 0)  y  (0, ∞). ♦

El wronskiano y la fórmula de Abel

Para motivar un resultado que necesitamos con el fin de demostrar  el Teorema 9.5.1.3, veamos qué se requiere para probar que {y₁, y₂} es un conjunto fundamental de soluciones de (9.5.1.20) en (a, b). Sea x₀ un punto arbitrario en (a, b), y suponga que y es una solución arbitraria de (9.5.1.20) en (a, b). Luego y es la solución única del problema de valor inicial

y″ + p(x)y′ + q(x)y = 0, y(x₀) = k₀, y′(x₀) = k₁;        (9.5.1.21)

es decir, k₀ y k₁ son los números obtenidos al evaluar y e y′ en x₀. Además, k₀ y k₁ pueden ser cualquier número real, ya que el teorema 9.5.1.1 implica que (9.5.1.21) tiene una solución sin importar cómo se elijan k₀ y k₁. Por lo tanto, {y₁, y₂} es un conjunto fundamental de soluciones de (9.5.1.20) en (a, b) si y solo si es posible escribir la solución de un problema de valor inicial arbitrario (9.5.1.21) como y = c₁y₁ + c₂y₂. Esto es equivalente a exigir que el sistema

tiene una solución (c₁, c₂) para cada elección de (k₀, k₁). Tratemos de resolver (9.5.1.22).

      Multiplicando la primera ecuación en (9.5.1.22) por y₂′(x₀) y la segunda por y₂(x₀) se obtiene

y restando la segunda ecuación aquí de la primera se obtiene

(y₁(x₀) y₂′(x₀) − y₁′(x₀) y₂(x₀))c₁ = y₂′(x₀)k₀ − y₂(x₀)k₁.        (9.5.1.23)

       Multiplicando la primera ecuación en (9.5.1.22) por y₁′(x₀) y la segunda por y₁(x₀) se obtiene

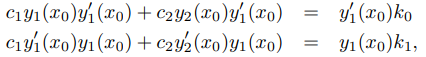
y restando aquí la primera ecuación de la segunda se obtiene

(y₁(x₀) y₂′(x₀) − y₁′(x₀) y₂(x₀))c₂ = y₁(x₀)k₁ − y₁′(x₀)k₀.        (9.5.1.24)

Si

y₁(x₀) y₂′(x₀) − y₁′(x₀) y₂(x₀) = 0,

es imposible satisfacer (9.5.1.23) y (9.5.1.24) (y por lo tanto (9.5.1.22)) a menos que k₀ y k₁ satisfagan

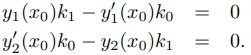
Por otro lado, si

y₁(x₀) y₂′(x₀) − y₁′(x₀) y₂(x₀) ≠ 0       (9.5.1.25)

podemos dividir (9.5.1.23) y (9.5.1.24) entre la cantidad de la izquierda para obtener

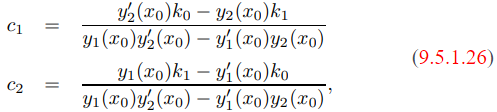
no importa cómo se elijan k₀ y k₁. Esto nos motiva a considerar condiciones en y₁ e y₂ que implican (9.5.1.25).

Teorema 9.5.1.4

Supongamos que p y q son continuas en (a, b), sean y₁ e y₂ soluciones de

y″ + p(x)y′ + q(x)y = 0        (9.5.1.27)

en (a, b), y definamos

W = y₁ y′₂ − y′₁ y₂.        (9.5.1.28)

Sea x₀ cualquier punto en (a, b). Entonces

Por lo tanto W no tiene ceros en (a, b) o W ≡ 0 en (a, b).  ♦

Demostración: 

Diferenciando (9.5.1.28), se obtiene

Como y₁ e y₂ satisfacen (9.5.1.27),

y₁″ = −py₁′ − qy₁   y   y₂″ = −py₂′ − qy₂.

Sustituyendo esto en (9.5.1.30), se obtiene

Por lo tanto W ′ + p(x)W = 0; es decir, W es la solución del problema de valor inicial

y ′ + p(x)y = 0,   y(x₀) = W(x₀)

Te dejamos comprobar por separación de variables que esto implica (9.5.1.29). Si W(x₀) ≠ 0, (9.5.1.29) implica que W no tiene ceros en (a, b), ya que una exponencial nunca es cero. Por otro lado, si W(x₀) = 0, (9.5.1.29) implica que W(x) = 0 para todo x en (a, b).  ◊

      La función W definida en (9.5.1.28) es el Wronskiano de {y₁, y₂}. La fórmula (9.5.1.29) es la fórmula de Abel.

      El wronskiano de {y₁, y₂} generalmente se escribe como el determinante       

Las expresiones en (9.5.1.26) para c₁ y c₂ se pueden escribir en términos de determinantes como

Si ha tomado álgebra lineal, puede reconocer esto como la regla de Cramer.

Ejemplo ilustrativo 9.5.1_5

Verifique la fórmula de Abel para las siguientes ecuaciones diferenciales y las soluciones correspondientes, de los ejemplos 9.5.1.1, 9.5.1.2 y 9.5.1.3:

Solución:

(a)  Como p ≡ 0, podemos verificar la fórmula de Abel mostrando que W es constante, lo cual es cierto, ya que

para todo x.

(b)  Nuevamente, dado que p ≡ 0, podemos verificar la fórmula de Abel mostrando que W es constante, lo cual es cierto, ya que

para todo x.

(c) Calcular el Wronskiano de y₁ = x²  y  y₂ = 1/x² produce directamente

      (9.5.1.31)

Para verificar la fórmula de Abel, reescribimos la ecuación diferencial como

se puede ver que p(x) = 1/x. Si x₀  y  x están en (−∞, 0) o en (0, ∞) entonces

por lo que la fórmula de Abel se convierte en

lo cual es consistente con (9.5.1.31).  ♦

      El siguiente teorema nos permitirá completar la demostración del Teorema 9.5.1.3.

Teorema 9.5.1.5

Suponga que p y q son continuas en un intervalo abierto (a, b), sean y₁ e y₂ soluciones de

y″ + p(x)y′ + q(x)y = 0        (9.5.1.32)

en (a, b), y sea W = y₁y₂′ − y₁′ y₂. Entonces y₁ e y₂ son linealmente independientes en (a, b) si y solo si W no tiene ceros en (a, b).  ♦

Demostración: Primero mostramos que si W(x₀) = 0 para algún x₀ en (a, b), entonces y₁ e y₂ son linealmente dependientes en (a, b). Sea I un subintervalo de (a, b) en el que y₁ no tiene ceros. (Si no existe tal subintervalo, y₁ ≡ 0 en (a, b), por lo que y₁ e y₂ son linealmente dependientes, y hemos terminado con esta parte de la prueba). Entonces y₂/y₁ se define en I, y

      (9.5.1.33)

Sin embargo, si W(x₀) = 0, el Teorema 9.5.1.4 implica que W ≡ 0 en (a, b). Por lo tanto (9.5.1.33) implica que (y₂/y₁)′ ≡ 0, entonces y₂/y₁ = c (constante) en I. Esto muestra que y₂(x) = cy₁(x) para todo x en I. Sin embargo, queremos mostrar que y₂(x) = cy₁(x) para todo x en (a, b). Sea Y = y₂ − cy₁. Entonces Y es una solución de (9.5.1.32) en (a, b) tal que Y ≡ 0 en I, y por lo tanto Y ′ ≡ 0 en I. En consecuencia, si x₀ se elige arbitrariamente en I entonces Y es una solución del problema de valor inicial

y″ + p(x)y′ + q(x)y = 0,  y(x₀) = 0,  y′(x₀) = 0,

lo que implica que Y ≡ 0 en (a, b), por el párrafo siguiente al Teorema 9.5.1.1. (Véase también el Ejercicio 24). Por lo tanto, y₂ − cy₁ ≡ 0 en (a, b), lo que implica que y₁ e y₂ no son linealmente independientes en (a, b).

      Ahora suponga que W no tiene ceros en (a, b). Entonces y₁ no puede ser idénticamente cero en (a, b) (¿por qué no?), y por lo tanto hay un subintervalo I de (a, b) en el que y₁ no tiene ceros. Dado que (9.5.1.33) implica que y₂/y₁ no es constante en I, y₂ no es un múltiplo constante de y₁ en (a, b). Un argumento similar muestra que y₁ no es un múltiplo constante de y₂ en (a, b) ya que

en cualquier subintervalo de (a, b) donde y₂ no tiene ceros. ♦

       Ahora podemos completar la demostración del Teorema 9.5.1.3. Del Teorema 9.5.1.5, dos soluciones y₁ e y₂ de (9.5.1.32) son linealmente independientes en (a, b) si y solo si W no tiene ceros en (a, b). Del Teorema 9.5.1.4 y los comentarios motivadores que lo preceden, {y₁, y₂} es un conjunto fundamental de soluciones de (9.5.1.32) si y solo si W no tiene ceros en (a, b). Por lo tanto, {y₁, y₂} es un conjunto fundamental para (9.5.1.32) en (a, b) si y solo si {y₁, y₂} es linealmente independiente en (a, b).  ♦

      El siguiente teorema resume las relaciones entre los conceptos discutidos en esta sección.

Teorema 9.5.1.6

Suponga que p y q son continuas en un intervalo abierto (a, b), sean y₁ e y₂ soluciones de

y″ + p(x)y′ + q(x)y = 0        (9.5.1.34)

en (a, b). Entonces las siguientes declaraciones son equivalentes; es decir, son todas verdaderas o todas falsas.

(a) La solución general de (9.5.1.34) en (a, b) es y = c₁y₁ + c₂y₂.
(b) {y₁, y₂} es un conjunto fundamental de soluciones de (9.5.1.34) en (a, b).
(c) {y₁, y₂} es linealmente independiente en (a, b).

(d) El wronskiano de {y₁, y₂} es distinto de cero en algún punto en (a, b).
(e) El wronskiano de {y₁, y₂} es distinto de cero en todos los puntos en (a, b).  ♦

      Podemos aplicar este teorema a una ecuación escrita como

P₀(x)y″ + P₁(x)y′ + P₂(x)y = 0

en un intervalo (a, b) donde P₀, P₁ y P₂ son continuos y P₀ no tiene ceros.

Teorema 9.5.1.7

Supongamos que c está en (a, b) y α y β son números reales, no ambos cero. Bajo los supuestos del Teorema 9.5.1.6, suponga que y₁ e y₂ son soluciones de (9.5.1.34) tales que

αy₁(c) + βy₁′ (c) = 0  y  αy₂(c) + βy₂′ (c) = 0.        (9.5.1.35)

Entonces {y₁, y₂} no es linealmente independiente en (a, b).  ♦

Prueba:  Dado que α y β no son cero, (9.5.1.35) implica que

y el Teorema 9.5.1.6 implica la conclusión establecida. ♦