| 9. Ecuaciones diferenciales | 9.6 Aplicaciones de ecuaciones lineales de segundo orden |
9.6.3 Los circuitos RLC
En esta sección consideramos el circuito RLC, que se muestra esquemáticamente en la Figura 9.6.3.1. Como veremos, el circuito RLC es un análogo eléctrico de un sistema de masa-resorte con amortiguamiento.
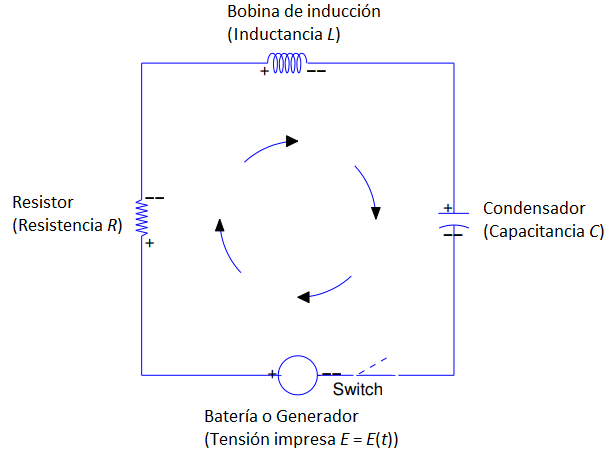
Figura 9.6.3.1 Un circuito RLC
No sucede nada mientras el interruptor (Switch) está abierto (línea discontinua). Cuando el interruptor está cerrado (línea continua) decimos que el circuito está cerrado. Las diferencias en el potencial eléctrico en un circuito cerrado hacen que fluya corriente en el circuito. La batería o generador de la figura 9.6.3.1 crea una diferencia de potencial eléctrico E = E(t) entre sus dos terminales, que hemos marcado arbitrariamente como positivo y negativo. (También podríamos intercambiar las marcas). Diremos que E(t) > 0 si el potencial en la terminal positiva es mayor que el potencial en la terminal negativa, E(t) < 0 si el potencial en la terminal terminal positiva es menor que el potencial en la terminal negativa, y E(t) = 0 si el potencial es el mismo en las dos terminales. Llamamos a E el voltaje impreso.
En cualquier tiempo t, la misma corriente fluye en todos los puntos del circuito. Denotamos corriente por I = I(t). Decimos que I(t) > 0 si la dirección del flujo es alrededor del circuito desde la terminal positiva de la batería o generador de regreso a la terminal negativa, como lo indican las flechas en la Figura 9.6.3.1 I(t)< 0 si el flujo es en la dirección opuesta, e I(t) = 0 si no fluye corriente en el tiempo t.
Las diferencias de potencial ocurren en la resistencia, la bobina de inducción y el capacitor en la Figura 9.6.3.1. Tenga en cuenta que los dos lados de cada uno de estos componentes también se identifican como positivo y negativo. La caída de tensión en cada componente se define como el potencial en el lado positivo del componente menos el potencial en el lado negativo. Esta terminología es algo engañosa, ya que “caída” sugiere una disminución, aunque los cambios en el potencial son cantidades con signo y, por lo tanto, pueden ser aumentos. Sin embargo, seguiremos la tradición y los llamaremos caídas de tensión. La caída de tensión en la resistencia de la figura 9.6.3.1 está dada por
VR = IR, (9.6.3.1)
donde I es corriente y R es una constante positiva, la resistencia del resistor. La caída de voltaje a través de la bobina de inducción está dada por
(9.6.3.2)
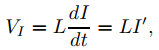
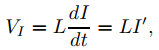
donde L es una constante positiva, la inductancia de la bobina.
Un condensador almacena carga eléctrica Q = Q(t), que está relacionada con la corriente en el circuito por la ecuación
(9.6.3.3)
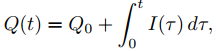
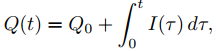
donde Q0 es la carga en el capacitor en t = 0. La caída de voltaje a través de un capacitor viene dada por
(9.6.3.4)
donde C es una constante positiva, la capacitancia del capacitor
La tabla 9.6.3.8 nombra las unidades para las cantidades que hemos discutido. Las unidades se definen de modo que
1 voltio = 1 amperio · 1 ohm
= 1 henrio · 1 amperio/segundo
= 1 culombio/ faradio
y
1 amperio = 1 culombio/segundo.
| Símbolo | Nombre | Unidad |
| E | Voltaje impreso | Voltio |
| I | Corriente | amperio |
| Q | Carga | culombio |
| R | Resistencia | ohm |
| L | Inductancia | henrio |
| C | Capacitancia | faradio |
Tabla 9.6.3.8. Unidades Eléctricas
Según la ley de Kirchhoff, la suma de las caídas de tensión en un circuito RLC cerrado es igual a la tensión aplicada. Por lo tanto, de (9.6.3.1), (9.6.3.2) y (9.6.3.4),
(9.6.3.5)
Esta ecuación contiene dos incógnitas, la corriente I en el circuito y la carga Q en el capacitor. Sin embargo, (9.6.3.3) implica que Q′ = I, por lo que (9.6.3.5) puede convertirse en la ecuación de segundo orden
(9.6.3.6)
en Q. Para encontrar la corriente que fluye en un circuito RLC, resolvemos (9.6.3.6) para Q y luego diferenciamos la solución para obtener I.
En las Secciones 9.6.1 y 9.6.2 encontramos la ecuación
my′′ + cy′ + ky = F(t) (9.6.3.7)
en relación con los sistemas de masa-resorte. Excepto por la notación, esta ecuación es la misma que (9.6.3.6). La correspondencia entre las cantidades eléctricas y mecánicas relacionadas con (9.6.3.6) y (9.6.3.7) se muestra en la Tabla 9.6.3.9
| Eléctrica | Mecánica |
| carga Q | desplazamiento y |
| corriente I | velocidad y′ |
| voltaje impreso E(t) | fuerza externa F(t) |
| inductancia L | masa m |
| resistencia R | amortiguación c |
| 1/capacitancia 1/C | constante de resorte k |
Tabla 9.6.3.9. Unidades Eléctricas y Mecánicas
La equivalencia entre (9.6.3.6) y (9.6.3.7) es un ejemplo de cómo las matemáticas unifican similitudes fundamentales en diversos fenómenos físicos. Como ya hemos estudiado las propiedades de las soluciones de (9.6.3.7) en las Secciones 9.6.1 y 9.6.2, podemos obtener resultados relativos a las soluciones de (9.6.3.6) simplemente cambiando la notación, de acuerdo con la Tabla 9.6.3.8.
Oscilaciones libres
Decimos que un circuito RLC está en oscilación libre si E(t) = 0 para t > 0, de modo que (9.6.3.6) se convierte en
(9.6.3.8)
La ecuación característica de (9.6.3.8) es
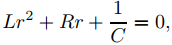
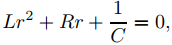
con raíces
y 
(9.6.3.9)
Aquí hay tres casos a considerar, todos análogos a los casos considerados en la Sección 9.6.2 para vibraciones libres de un sistema masa-resorte amortiguado.
CASO 1. La oscilación está subamortiguada si 
En este caso, r1 y r2 en (9.6.3.9) son conjugados complejos, que escribimos como
y 
donde
La solución general de (9.6.3.8) es
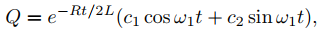
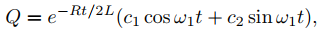
Que podemos escribir como
(9.6.3.10)
donde
Acosφ = c1, y Asenφ = c2.
En el caso idealizado donde R = 0, la solución (9.6.3.10) se reduce a
que es análogo al movimiento armónico simple de un sistema masa-resorte no amortiguado en vibración libre.
Los circuitos RLC reales suelen estar subamortiguados, por lo que el caso que acabamos de considerar es el más importante. Sin embargo, para completar, consideraremos las otras dos posibilidades.
CASO 2. La oscilación está sobreamortiguada si 
En este caso, los ceros r1 y r2 del polinomio característico son reales, con r1 < r2 < 0 (ver (9.6.3.9)), y la solución general de (9.6.3.8) es
(9.6.3.11)
CASO 3. La oscilación está críticamente amortiguada si 
En este caso, r1 = r2 = −R/2L y la solución general de (9.6.3.8) es
(9.6.3.12)
Si R ≠ 0, las exponenciales en (9.6.3.10), (9.6.3.11) y (9.6.3.12) son negativas, por lo que la solución de cualquier problema de valor inicial homogéneo
tiende a cero exponencialmente cuando t → ∞. Por lo tanto, todas estas soluciones son transitorias, en el sentido definido en la Sección 9.6.2 en la discusión de vibraciones forzadas de un sistema masa-resorte con amortiguamiento.
Ejemplo ilustrativo 9.6.3.1
En t = 0, fluye una corriente de 2 amperios en un circuito RLC con resistencia R = 40 ohmios, inductancia L = 0,2 henrios y capacitancia C = 10−5 faradios. Encuentre la corriente que fluye en el circuito en t > 0 si la carga inicial en el capacitor es de 1 culombio. Suponga que E(t) = 0 para t > 0.
Solución:
La ecuación para la carga Q es
o
Q′′ + 200Q′ + 50000Q = 0. (9.6.3.13)
Por lo tanto debemos resolver el problema de valor inicial
Q′′ + 200Q′ + 50000Q = 0, Q(0) = 1, Q′(0) = 2. (9.6.3.14)
La corriente deseada es la derivada de la solución de este problema de valor inicial.
La ecuación característica de (9.6.3.13) es
r2 + 200r + 50000 = 0,
que tiene ceros complejos r = −100 ± 200i. Por tanto, la solución general de (9.6.3.13) es
Q = e−100t(c1 cos200t + c2 sen200t). (9.6.3.15)
Diferenciar esto y recopilar términos similares produce
Q′ = −e−100t [(100c1 − 200c2) cos200t + (100c2 + 200c1) sen200t]. (9.6.3.16)
Para encontrar la solución del problema de valor inicial (9.6.3.14), establecemos t = 0 en (9.6.3.15) y (9.6.3.16) para obtener
c1 = Q(0) = 1 y − 100c1 + 200c2 = Q′(0) = 2;
por lo tanto, c1 = 1 y c2 = 51/100, entonces
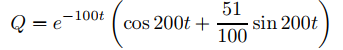
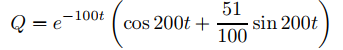
es la solución de (9.6.3.14). Diferenciando esto se obtiene
I = e−100t(2cos200t − 251sen200t). ♦
Oscilaciones Forzadas Con Amortiguación
Un problema de valor inicial para (9.6.3.6) tiene la forma
(9.6.3.17)
donde Q0 es la carga inicial en el capacitor e I0 es la corriente inicial en el circuito. Ya vimos que si E ≡ 0 entonces todas las soluciones de (9.6.3.17) son transitorias. Si E ≠ 0, sabemos que la solución de (9.6.3.17) tiene la forma Q = Qc + Qp, donde Qc satisface la ecuación complementaria y tiende a cero exponencialmente cuando t → ∞ para cualquier condición inicial, mientras que Qp depende solo en E y es independiente de las condiciones iniciales. Como en el caso de las oscilaciones forzadas de un sistema masa-resorte con amortiguamiento, llamamos Qp a la carga de estado estacionario en el capacitor del circuito RLC. Como I = Q′ = Q′c + Q′p y Q′c también tiende a cero exponencialmente cuando t → ∞, decimos que Ic = Q′c es la corriente transitoria e Ip = Q′p es la corriente de estado estable . En la mayoría de las aplicaciones, solo nos interesa la carga y la corriente de estado estable.
Ejemplo ilustrativo 9.6.3.2
Encuentre la forma amplitud-fase de la corriente de estado estable en el circuito RLC de la figura 9.6.3.1 si el voltaje aplicado, proporcionado por un generador de corriente alterna, es E(t) = E0 cosωt.
Solución:
Primero encontraremos la carga de estado estacionario en el capacitor como una solución particular de
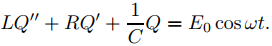
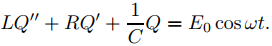
Para hacer esto, simplemente reinterpretaremos un resultado obtenido en la Sección 9.6.2, donde encontramos que la solución de estado estacionario de
my′′ + cy′ + ky = F0 cosωt
es
donde
y 
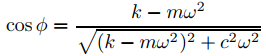
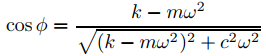
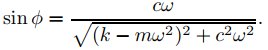
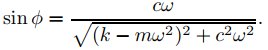
(Ver Ecuaciones (9.6.2.14) y (9.6.2.15).) Haciendo los cambios apropiados en los símbolos (según la Tabla 2) se obtiene la carga de estado estacionario
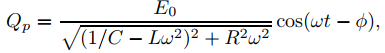
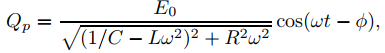
donde
y 
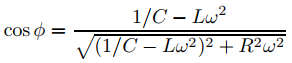
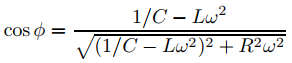
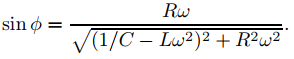
Por lo tanto, la corriente de estado estable en el circuito es
♦