| 9. Ecuaciones diferenciales | 9.5 Ecuaciones lineales de segundo orden |
9.5.5 El método de coeficientes indeterminados II
En esta sección consideramos la ecuación de coeficientes constantes
ay′′ + by′ + cy = eλx (P(x) cosωx + Q(x) senωx) (9.5.5.1)
donde λ y ω son números reales, ω ≠ 0, y P y Q son polinomios. Queremos encontrar una solución particular de (9.5.5.1). Al igual que en la Sección 9.5.4, el procedimiento que utilizaremos se denomina método de coeficientes indeterminados.
Funciones forzadas sin factores exponenciales
Comenzamos con el caso donde λ = 0 en (9.5.5.1); por lo tanto, queremos encontrar una solución particular de
ay′′ + by′ + cy = P(x) cosωx + Q(x) senωx, (9.5.5.2)
donde P y Q son polinomios.
Derivando xr cosωx y xr senωx se obtiene
y
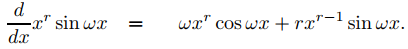
Esto implica que si
yp = A(x) cosωx + B(x) senωx
donde A y B son polinomios, entonces
ayp′′ + byp′ + cyp = F(x) cosωx + G(x) senωx,
donde F y G son polinomios con coeficientes que se pueden expresar en términos de los coeficientes de A y B. Esto sugiere que tratamos de elegir A y B para que F = P y G = Q, respectivamente. Entonces yp será una solución particular de (9.5.5.2). El siguiente teorema nos dice cómo elegir la forma adecuada para yp. Para la demostración ver el Ejercicio 37.
Teorema 9.5.5.1
Supongamos que ω es un número positivo y P y Q son polinomios. Sea k el mayor de los grados de P y Q. Entonces la ecuación
ay′′ + by′ + cy = P(x) cosωx + Q(x) senωx
tiene una solución particular
yp = A(x) cosωx + B(x) senωx, (9.5.5.3)
donde
A(x) = A0 + A1x + · · · + Akxk y B(x) = B0 + B1x + · · · + Bkxk,
siempre que cosωx y senωx no sean soluciones de la ecuación complementaria. las soluciones de
a(y′′ + ω2y) = P(x) cosωx + Q(x) senωx
(para las cuales cosωx y senω son soluciones de la ecuación complementaria) son de la forma (9.5.5.3), donde
A(x) = A0x + A1x2 + · · · + Akxk + 1 y B(x) = B0x + B1x2 + · · · + Bkxk + 1. ♦
Para un análogo de este teorema aplicable a (9.5.5.1), vea el Ejercicio 38.
Ejemplo ilustrativo 9.5.5.1
Encuentre una solución particular de
y′′ − 2y′ + y = 5 cos2x + 10 sen2x. (9.5.5.4)
Solución:
En (9.5.5.4), los coeficientes de cos2x y sen2x son ambos polinomios de grado cero (constantes).
Por lo tanto, el Teorema 9.5.5.1 implica que (9.5.5.4) tiene una solución particular
yp = A cos2x + B sen2x.
Como
yp′ = −2Asen2x + 2B cos2x y yp′′ = −4(Acos2x + B sen2x),
reemplazando y por yp en (9.5.5.4), se obtiene
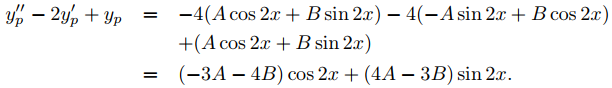
Igualando los coeficientes de cos2x y sen2x aquí con los coeficientes correspondientes del lado derecho de (9.5.5.4) se muestra que yp es una solución de (9.5.5.4) si
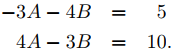
Resolviendo estas ecuaciones se obtiene A = 1, B = −2. Por lo tanto
yp = cos2x − 2sen2x
es una solución particular de (9.5.5.4). ♦
Ejemplo ilustrativo 9.5.5.2
Encuentre una solución particular de
y′′ + 4y = 8 cos2x + 12 sen2x. (9.5.5.5)
Solución:
El procedimiento utilizado en el Ejemplo 9.5.5.1 no funciona aquí; sustituyendo yp = Acos2x + Bsen2x por y en (9.5.5.5) se obtiene
yp′′ + 4yp = −4(Acos2x + Bsen2x) + 4(Acos2x + Bsen2x) = 0
para cualquier elección de A y B, ya que cos2x y sen2x son ambas soluciones de la ecuación complementaria para (9.5.5.5). Estamos tratando con el segundo caso mencionado en el Teorema 9.5.5.1 y, por lo tanto, deberíamos intentar una solución particular de la forma
yp = x(Acos2x + Bsen2x). (9.5.5.6)
entonces
yp′ = Acos2x + Bsen2x + 2x(−Asen2x + Bcos2x)
y
yp′′ = −4Asen2x + 4Bcos2x − 4x(Acos2x + Bsen2x)
= −4Asen2x + 4Bcos2x − 4yp (ver (9.5.5.6)),
entonces
yp′′ + 4yp = −4Asen2x + 4Bcos2x.
Por lo tanto yp es solución de (9.5.5.5) si
−4Asen2x + 4Bcos2x = 8cos2x + 12sen2x,
lo cual se cumple si A = −3 y B = 2. Por lo tanto
yp = −x(3cos2x − 2sen2x)
es una solución particular de (9.5.5.5). ♦
Ejemplo ilustrativo 9.5.5.3
Encuentre una solución particular de
y′′ + 3y′ + 2y = (16 + 20x) cosx + 10 senx. (9.5.5.7)
Solución:
Los coeficientes de cosx y senx en (9.5.5.7) son polinomios de grado uno y cero, respectivamente. Por tanto, el Teorema 9.5.5.1 nos dice que busquemos una solución particular de (9.5.5.7) de la forma
yp = (A0 + A1x) cosx + (B0 + B1x) senx. (9.5.5.8)
Entonces
yp′ = (A1 + B0 + B1x) cosx + (B1 − A0 − A1x) sen x (9.5.5.9)
y
yp′′ = (2B1 − A0 − A1x) cosx − (2A1 + B0 + B1x) senx, (9.5.5.10)
por lo que
(9.5.5.11)
La comparación de los coeficientes de xcosx, xsenx, cosx y senx aquí con los coeficientes correspondientes en (9.5.5.7) muestra que yp es una solución de (9.5.5.7) si
Resolviendo las dos primeras ecuaciones se obtiene A1 = 2, B1 = 6. Sustituyendo estos valores en las dos últimas ecuaciones, se obtiene
Resolviendo estas ecuaciones se obtiene A0 = 1, B0 = −1. Sustituyendo A0 = 1, A1 = 2, B0 = −1, B1 = 6 en (9.5.5.8) se ve que
yp = (1 + 2x) cosx − (1 − 6x) senx
es una solución particular de (9.5.5.7). ♦
Una observación útil
En (9.5.5.9), (9.5.5.10) y (9.5.5.11) los polinomios que multiplican en x se pueden obtener reemplazando A0, A1, B0 y B1 por B0, B1, −A0 y −A1, respectivamente, en los polinomios multiplicando cos x. Un resultado análogo se aplica en general, como sigue (Ejercicio 36).
Teorema 9.5.5.2
Si
yp = A(x) cosωx + B(x) senωx,
donde A(x) y B(x) son polinomios con coeficientes A0. . . , Ak y B0, . . . , Bk, entonces los polinomios que multiplican senωx en
yp′ , yp′′, ayp′′ + byp′ + cyp y yp′′ + ω2yp
se pueden obtener reemplazando A0. . . , Ak por B0, . . . , Bk y B0, . . . , Bk por −A0, . . ., −Ak en los polinomios correspondientes multiplicando cosωx. ♦
No usaremos este teorema en nuestros ejemplos, pero le recomendamos que lo use para verificar sus manipulaciones cuando trabaje en los ejercicios.
Ejemplo ilustrativo 9.5.5.4
Encuentre una solución particular de
y′′ + y = (8 − 4x)cosx − (8 + 8x)senx. (9.5.5.12)
Solución:
De acuerdo con el Teorema 9.5.5.1, debemos buscar una solución particular de la forma
yp = (A0x + A1x2) cosx + (B0x + B1x2) senx, (9.5.5.13)
ya que cosx y senx son soluciones de la ecuación complementaria. Sin embargo, intentemos
yp = (A0 + A1x) cosx + (B0 + B1x) senx (9.5.5.14)
primero, para que pueda ver por qué no funciona. De (9.5.5.10),
yp′′ = (2B1 − A0 − A1x) cosx − (2A1 + B0 + B1x) senx,
lo que junto con (9.5.5.14) implica que
yp′′ + yp = 2B1cosx − 2A1senx.
Dado que el lado derecho de esta ecuación no contiene xcosx o xsenx, (9.5.5.14) no puede satisfacer (9.5.5.12) sin importar cómo elijamos A0, A1, B0 y B1.
Ahora sea yp como en (9.5.5.13). Entonces
y
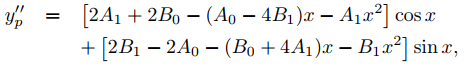
por lo que
yp′′ + yp = (2A1 + 2B0 + 4B1x) cosx + (2B1 − 2A0 − 4A1x) senx.
La comparación de los coeficientes de cosx y senx aquí con los coeficientes correspondientes en (9.5.5.12) muestra que yp es una solución de (9.5.5.12) si
La solución de este sistema es A1 = 2, B1 = −1, A0 = 3, B0 = 2. Por lo tanto
yp = x [(3 + 2x) cosx + (2 − x) senx]
es una solución particular de (9.5.5.12). ♦
Funciones forzadas con factores exponenciales
Para encontrar una solución particular de
ay′′ + by′ + cy = eλx (P(x) cosωx + Q(x) senωx) (9.5.5.15)
cuando λ ≠ 0, recordamos de la Sección 9.5.4 que sustituir y = ueλx en (9.5.5.15) producirá una ecuación de coeficientes constantes para u con la función forzada P(x) cosωx + Q(x) senωx. Podemos encontrar una solución particular de esta ecuación mediante el procedimiento que usamos en los ejemplos 9.5.5.1 a 9.5.5.4. Entonces yp = upeλx es una solución particular de (9.5.5.15).
Ejemplo ilustrativo 9.5.5.5
Encuentre una solución particular de
y′′ − 3y′ + 2y = e−2x [2 cos3x − (34 − 150x) sen3x]. (9.5.5.16)
Solución:
Sea y = ue−2x. Entonces
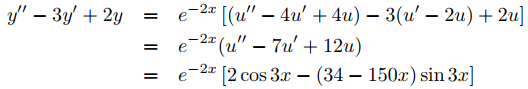
si
u′′ − 7u′ + 12u = 2 cos3x − (34 − 150x) sen3x. (9.5.5.17)
Como cos3x y sen3x no son soluciones de la ecuación complementaria
u′′ − 7u′ + 12u = 0,
El Teorema 9.5.5.1 nos dice que busquemos una solución particular de (9.5.5.17) de la forma
up = (A0 + A1x) cos3x + (B0 + B1x) sen3x. (9.5.5.18)
Entonces
u′p = (A1 + 3B0 + 3B1x) cos3x + (B1 − 3A0 − 3A1x) sen3x
y
u′′p = (−9A0 + 6B1 − 9A1x) cos3x − (9B0 + 6A1 + 9B1x) sen3x,
por consiguiente
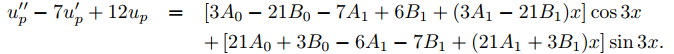
La comparación de los coeficientes de xcos3x, xsen3x, cos3x y sen3x aquí con los coeficientes correspondientes en el lado derecho de (9.5.5.17) muestra que up es una solución de (9.5.5.17) si
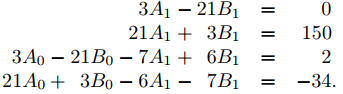(9.5.5.19)
Resolviendo las dos primeras ecuaciones se obtiene A1 = 7, B1 = 1. Sustituyendo estos valores en las dos últimas ecuaciones de (9.5.5.19) se obtiene
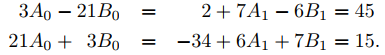
Resolviendo este sistema se obtiene A0 = 1, B0 = −2. Sustituyendo A0 = 1, A1 = 7, B0 = −2 y B1 = 1 en (9.5.5.18) muestra que
up = (1 + 7x) cos3x − (2 − x) sen3x
es una solución particular de (9.5.5.17). Por lo tanto
yp = e−2x [(1 + 7x) cos3x − (2 − x) sen3x]
es una solución particular de (9.5.5.16). ♦
Ejemplo ilustrativo 9.5.5.6
Encuentre una solución particular de
y′′ + 2y′ + 5y = e−x [(6 − 16x) cos2x − (8 + 8x) sen2x]. (9.5.5.20)
Solución:
Sea y = ue−x. Entonces
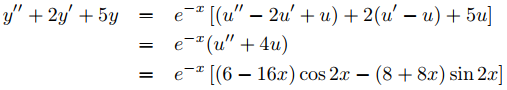
si
u′′ + 4u = (6 − 16x) cos2x − (8 + 8x) sen2x. (9.5.5.21)
Como cos2x y sen2x son soluciones de la ecuación complementaria
u′′ + 4u = 0,
El Teorema 9.5.5.1 nos dice que busquemos una solución particular de (9.5.5.21) de la forma
up = (A0x + A1x2) cos2x + (B0x + B1x2) sen2x.
Entonces
y
de tal forma que
u′′p + 4up = (2A1 + 4B0 + 8B1x) cos2x + (2B1 − 4A0 − 8A1x) sen2x.
Igualando los coeficientes de xcos2x, xsen2x, cos2x y sen2x aquí con los coeficientes correspondientes en el lado derecho de (9.5.5.21) muestra que up es una solución de (9.5.5.21) si
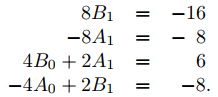(9.5.5.22)
La solución de este sistema es A1 = 1, B1 = −2, B0 = 1, A0 = 1. Por lo tanto
p = x[(1 + x) cos2x + (1 − 2x) sen2x]
es una solución particular de (9.5.5.21), y
yp = xe−x [(1 + x) cos2x + (1 − 2x) sen2x]
es una solución particular de (9.5.5.20). ♦
También puede encontrar una solución particular de (9.5.5.20) sustituyendo
yp = xe−x(A0 + A1x) cos2x + (B0 + B1x) sen2x.
para y en (9.5.5.20) e igualando los coeficientes de xe−x cos2x, xe−x sen2x, e−x cos2x y e−xsen2x en la expresión resultante para
yp” + 2yp′ + 5yp
con los coeficientes correspondientes en el lado derecho de (9.5.5.20). (Ver Ejercicio 38). Esto conduce al mismo sistema (9.5.5.22) de ecuaciones para A0, A1, B0 y B1 que obtuvimos en el Ejemplo 9.5.5.6. Sin embargo, si prueba este enfoque, verá que derivar (9.5.5.22) de esta manera es mucho más tedioso que la forma en que lo hicimos en el Ejemplo 9.5.5.6.