| 9. Ecuaciones diferenciales |
9.11 Problemas de valores en la frontera y expansiones de Fourier. Objetivos de aprendizaje:
EN ESTE CAPÍTULO desarrollamos representaciones en serie de funciones que se utilizarán para resolver ecuaciones diferenciales parciales en el Capítulo 9.12.
La SECCIÓN 9.11.1 trata de cinco problemas de valores en la frontera para la ecuación diferencial
y″ + λy = 0.
Están relacionados con problemas en ecuaciones diferenciales parciales que se discutirán en el Capítulo 9.12. Definimos qué se entiende por valores propios y funciones propias de los problemas de valores en la frontera, y mostramos que las funciones propias tienen una propiedad llamada ortogonalidad.
La SECCIÓN 9.11.2 introduce las series de Fourier, que son expansiones en términos de senos y cosenos de funciones dadas.
La SECCIÓN 9.11.3 trata de desarrollos de funciones en términos de las funciones propias de cuatro de los problemas de valores propios discutidos en la Sección 9.11.1. Todos están relacionados con la serie de Fourier discutida en la Sección 9.11.2.
9.11.1 PROBLEMAS DE VALOR PROPIO PARA y″ + λy = 0
En el Capítulo 9.12 estudiaremos ecuaciones diferenciales parciales que surgen en problemas de conducción de calor, propagación de ondas y teoría del potencial. El propósito de este capítulo es desarrollar las herramientas necesarias para resolver estas ecuaciones. En esta sección consideramos los siguientes problemas, donde λ es un número real y L > 0:
Problema 1: y″ + λy = 0, y(0) = 0, y(L) = 0
Problema 2: y″ + λy = 0, y′(0) = 0, y′(L) = 0
Problema 3: y″ + λy = 0, y(0) = 0, y′(L) = 0
Problema 4: y″ + λy = 0, y′(0) = 0, y(L) = 0
Problema 5: y″ + λy = 0, y(−L) = y(L), y′(−L) = y′(L)
En cada problema, las condiciones que siguen a la ecuación diferencial se denominan condiciones de contorno (o de frontera). Observe que las condiciones de contorno del problema 5, a diferencia de las de los problemas 1 a 4, no requieren que y o y′ sean cero en los puntos de contorno, sino que y tiene el mismo valor en x = ±L, y que y′ tiene el mismo valor en x = ±L. Decimos que las condiciones de contorno en el Problema 5 son periódicas.
Obviamente, y ≡ 0 (la solución trivial) es una solución de los Problemas 1-5 para cualquier valor de λ. Para la mayoría de los valores de λ, no hay otras soluciones. La pregunta interesante es esta:
¿Para qué valores de λ el problema tiene soluciones no triviales y cuáles son?
Un valor de λ para el cual el problema tiene una solución no trivial es un valor propio del problema, y las soluciones no triviales son funciones propias-λ, o funciones propias asociadas con λ. Tenga en cuenta que un múltiplo constante distinto de cero de una función propia λ es nuevamente una función propia λ.
Los problemas del 1 al 5 se llaman problemas de valores propios. Resolver un problema de valores propios significa encontrar todos sus valores propios y funciones propias asociadas. Tomaremos como dado aquí que todos los valores propios de los problemas 1-5 son números reales. Esto se demuestra en un marco más general en la Sección 9.13.2.
Teorema 9.11.1.1
Los problemas 1 a 5 no tienen valores propios negativos. Además, λ = 0 es un valor propio de los problemas 2 y 5, con la función propia asociada y0 = 1, pero λ = 0 no es un valor propio de los problemas 1, 3 o 4. ♦
Prueba
Consideramos los problemas 1 a 4 y le dejamos el problema 5 a usted (Ejercicio 1).
Si y″ + λy = 0, entonces y(y″ + λy) = 0, de tal manera que
por lo tanto,
(9.11.1.1)
efectuando integración por partes, se obtiene
(9.11.1.2)
Sin embargo, si y satisface cualquiera de las condiciones de contorno de los problemas 1 a 4, entonces
y(L) y′(L) − y(0) y′(0) = 0;
por tanto, (9.11.1.1) y (9.11.1.2) implican que
Si 
entonces 
Por tanto, λ ≥ 0 y, si λ = 0, entonces y′(x) = 0 para todo x en (0, L) (¿por qué?), y y es constante en (0, L). Cualquier función constante satisface las condiciones de contorno del Problema 2, por lo que λ = 0 es un valor propio del Problema 2 y cualquier función constante distinta de cero es una función propia asociada. Sin embargo, la única función constante que satisface las condiciones de contorno de los problemas 1, 3 o 4 es y ≡ 0. Por lo tanto, λ = 0 no es un valor propio de ninguno de estos problemas. ◊
Ejemplo ilustrativo 9.11.1.1 (Problema 1)
Resolver el problema de valor propio
y″ + λy = 0, y(0) = 0, y(L) = 0. (9.11.1.3)
Solución:
Del Teorema 9.11.1.1, cualquier valor propio de (9.11.1.3) debe ser positivo. Si y satisface (9.11.1.3) con λ > 0, entonces
donde c1 y c2 son constantes. La condición de frontera y(0) = 0 implica que c1 = 0. Por lo tanto y = c2 sen√λx. Ahora, la condición de frontera y(L) = 0 implica que c2sen√λL = 0. Para hacer que c2sen√λL = 0 con c2 ≠ 0, debemos elegir √λ = nπ/L, donde n es un valor positivo entero. Por lo tanto, λn = n2π2/L2 es un valor propio y
yn = sen(nπx/L)
es una función propia asociada. ♦
Para referencia futura, expresamos el resultado del Ejemplo 9.11.1.1 como un teorema.
Teorema 9.11.1.2
El problema de valores propios
y″ + λy = 0, y(0) = 0, y(L) = 0
tiene infinitos valores propios positivos λn = n2π2/L2, con funciones propias asociadas
No hay otros valores propios. ♦
Le dejamos a usted probar el siguiente teorema sobre el Problema 2 mediante un argumento como el del Ejemplo 9.11.1.1 (Ejercicio 17).
Teorema 9.11.1.3
El problema de valores propios
y″ + λy = 0, y′(0) = 0, y′(L) = 0
tiene el valor propio λ0 = 0, con función propia asociada y0 = 1, e infinitos valores propios positivos λn = n2π2/L2, con funciones propias asociadas
No hay otros valores propios. ♦
Ejemplo ilustrativo 9.11.1.2 (Problema 3)
Resolver el problema de valor propio
y″ + λy = 0, y(0) = 0, y′(L) = 0 (9.11.1.4)
Solución:
Del Teorema 9.11.1.1, cualquier valor propio de (9.11.1.4) debe ser positivo. Si y satisface (9.11.1.4) con λ > 0, entonces
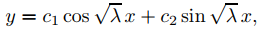
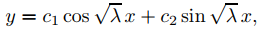
donde c1 y c2 son constantes. La condición de frontera y(0) = 0 implica que c1 = 0. Por lo tanto, y = c2sen√λx. Por lo tanto, y′ = c2√λcos√λx y la condición de frontera y′(L) = 0 implica que c2 cos√λL = 0. Para hacer c2cos√λL = 0 con c2 ≠ 0 debemos elegir
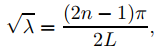
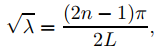
aquí n es un entero positivo. Entonces λn = (2n − 1)2π2/4L2 es un valor propio y
es una función propia asociada. ♦
Para futuras referencias, expresamos el resultado del Ejemplo 9.11.1.2 como un teorema.
Teorema 9.11.1.4
El problema de valores propios
y″ + λy = 0, y(0) = 0, y′(L) = 0
tiene infinitos valores propios positivos λn = (2n − 1)2π2/4L2, con funciones propias asociadas
No hay otros valores propios. ♦
Le dejamos a usted probar el siguiente teorema sobre el Problema 4 mediante un argumento como el del Ejemplo 9.11.1.2 (Ejercicio 18).
Teorema 9.11.1.5
El problema de valores propios
y″ + λy = 0, y′(0) = 0, y(L) = 0
tiene infinitos valores propios positivos λn = (2n − 1)2π2/4L2, con funciones propias asociadas
No hay otros valores propios. ♦
Ejemplo ilustrativo 9.11.1.3 (Problema 5)
Resolver el problema de valor propio
y″ + λy = 0, y(−L) = y(L), y′(−L) = y′(L) (9.11.1.5)
Solución;
Del Teorema 9.11.1.1, λ = 0 es un valor propio de (9.11.1.5) con función propia asociada y0 = 1, y cualquier otro valor propio debe ser positivo. Si y satisface (9.11.1.5) con λ > 0, entonces
y = c1cos√λx + c2sen√λx, (9.11.1.6)
donde c1 y c2 son constantes. La condición de frontera y(−L) = y(L) implica que
c1cos(−√λL) + c2sen(−√λL) = c1cos √λL + c2sen√λL. (9.11.1.7)
Ya que
cos(−√λL) = cos√λL y sen(−√λL) = − sen√λL, (9.11.1.8)
(9.11.1.7) implica que
c2sen√λL = 0. (9.11.1.9)
Diferenciando (9.11.1.6), se obtiene
La condición de frontera y′(−L) = y′(L) implica que
y (9.11.1.8) implica que
c1sen√λL = 0. (9.11.1.10)
Las ecuaciones (9.11.1.9) y (9.11.1.10) implican que c1 = c2 = 0 a menos que √λ = nπ/L, donde n es un número entero positivo. En este caso, (9.11.1.9) y (9.11.1.10) se cumplen para c1 y c2 arbitrarios. El valor propio determinado de esta manera es λn = n2π2/L2, y cada valor propio tiene las funciones propias asociadas linealmente independientes
♦
Teorema 9.11.1.6
El problema de valores propios
y″ + λy = 0, y(−L) = y(L), y′(−L) = y(−L)
tiene el valor propio λ0 = 0, con función propia asociada y0 = 1 e infinitos valores propios positivos λn = n2π2/L2, con funciones propias asociadas
No hay otros valores propios. ♦
Ortogonalidad
Decimos que dos funciones integrables f y g son ortogonales en un intervalo [a, b] si
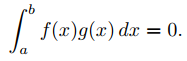
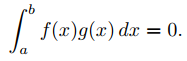
Más generalmente, decimos que las funciones φ1, φ2, . . . , φn , . . . (finita o infinitamente) son ortogonales en [a, b] si
para i ≠ j.
La importancia de la ortogonalidad quedará clara cuando estudiemos las series de Fourier en las próximas dos secciones.
Ejemplo ilustrativo 9.11.1.4
Demuestre que las funciones propias
(9.11.1.11)
del Problema 5 son ortogonales en [−L, L].
Solución:
Debemos demostrar que
(9.11.1.12)
siempre que f y g sean funciones distintas de (9.11.1.11). Si r es cualquier entero distinto de cero, entonces
(9.11.1.13)
y
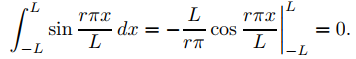
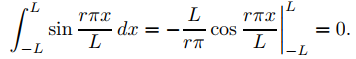
Por lo tanto (9.11.1.12) se cumple si f ≡ 1 y g es cualquier otra función en (9.11.1.11).
Si f (x) = cosmπx/L y g(x) = cosnπx/L donde m y n son enteros positivos distintos, entonces
(9.11.1.14)
Para evaluar esta integral, usamos la identidad
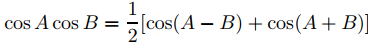
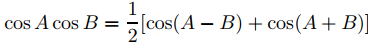
con A = mπx/L y B = nπx/L. Entonces (9.11.1.14) se convierte en
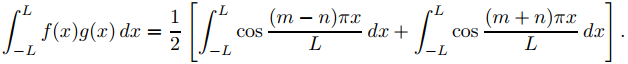
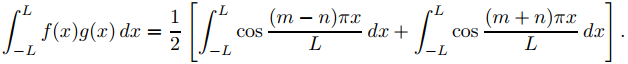
Dado que m − n y m + n son enteros distintos de cero, (9.11.1.13) implica que las integrales de la derecha son ambas cero. Por lo tanto (9.11.1.12) es verdadera en este caso.
Si f (x) = senmπx/L y g(x) = sennπx/L donde m y n son enteros positivos distintos, entonces
(9.11.1.15)
Para evaluar esta integral, usamos la identidad
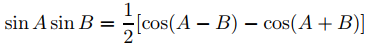
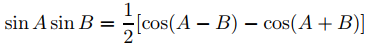
con A = mπx/L y B = nπx/L. Entonces (9.11.1.15) se convierte en
Si f (x) = senmπx/L y g(x) = cosnπx/L donde m y n son números enteros positivos (no necesariamente distintos), entonces
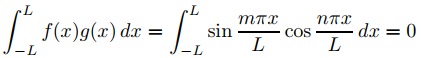
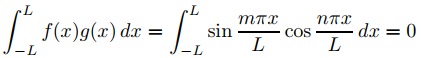
porque el integrando es una función impar y los límites son simétricos respecto a x = 0. ♦
En los Ejercicios 19 a 22 le piden verificar que las funciones propias de los Problema 1 a 4 son ortogonales en [0, L]. Sin embargo, esto también se deriva de un teorema general que demostraremos en el Capítulo 9.13.