| 5.1 La integral y Técnicas de integración | Ejercicios propuestos para el Capitulo 5.1 |
5.1 Aproximando áreas: Objetivos de aprendizaje
Sección 5.1.1 Usar la notación sigma (sumatoria) para calcular sumas de potencias de enteros.
Sección 5.1.2. Usar la suma de áreas rectangulares para aproximar el área bajo una curva.
Sección 5.1.3. Usar sumas de Riemann para aproximar el área.
Arquímedes estaba fascinado con el cálculo de las áreas de superficies que presentan variadas formas, en otras palabras, de calcular la cantidad de espacio encerrado por la forma. Utilizó un proceso que se conoce como el método de exhaución (“agotamiento”), que utiliza formas cada vez más pequeñas, cuyas áreas se pueden calcular exactamente, para llenar una región irregular y, por lo tanto, obtener aproximaciones cada vez más cercanas al área total. En este proceso, un área delimitada por curvas se rellena con rectángulos, triángulos u otras figuras geométricas con fórmulas de área conocida. Estas áreas se suman para aproximar el área de la región estudiada.
En esta sección, desarrollamos técnicas para aproximar el área entre una curva, definida por una función f (x), y el eje x en un intervalo cerrado [a, b]. Al igual que Arquímedes, primero aproximamos el área bajo la curva usando formas de área conocida (en nuestro caso, rectángulos). Al usar rectángulos cada vez más pequeños, nos acercamos cada vez más al área. Tomar un límite nos permite calcular el área exacta bajo de la curva.
Comencemos presentando alguna notación para facilitar los cálculos. Luego consideramos el caso cuando f (x) es continuo y no negativo. Más adelante en el capítulo, relajamos algunas de estas restricciones y desarrollamos técnicas que se aplican en casos más generales.
Notación Sigma (sumatoria)
Como se mencionó, utilizaremos formas de área conocida para aproximar el área de una región irregular limitada por curvas. Este proceso a menudo requiere sumar largas cadenas de números. Para que sea más fácil escribir estas sumas largas, vemos aquí una nueva notación, llamada notación sigma (también conocida como notación de suma). La letra mayúscula griega Σ, sigma, se utiliza para expresar sumas largas de valores en una forma compacta. Por ejemplo, si queremos agregar todos los enteros del 1 al 20 sin notación sigma, tenemos que escribir
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19 + 20.
Probablemente podríamos dejar de escribir un par de términos (designados por puntos suspensivos) y dar la suma como
1 + 2 + 3 + 4 + ⋯ + 19 + 20,
lo que es mejor, pero todavía engorroso. Con la notación sigma, escribimos esta suma como


que es mucho más compacto.
Por lo general, la notación sigma se presenta en la forma


donde aᵢ describe los términos que se agregarán, y la i se llama índice. Cada término se evalúa, luego sumamos todos los valores, comenzando con el valor cuando i = 1 y terminando con el valor cuando i = n.
Por ejemplo, una expresión como


se interpreta como s₂ + s₃ + s₄ + s₅ + s₆ + s₇. Tenga presente que el índice se usa solo para realizar un seguimiento de los términos que se agregarán, no se tiene en cuenta en el cálculo de la suma misma. De tal modo que el índice se denomina variable ficticia. Podemos usar cualquier letra que nos guste para el índice. Típicamente, los matemáticos usan i, j, k, m y n para los índices..
Ejemplo ilustrativo 5.1_1. Usando la notación Sigma
a. Escriba en notación sigma y evalúe la suma de los términos de la forma 3i para i = 1, 2, 3, 4, 5.
b. Escriba la siguiente suma en notación sigma: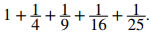
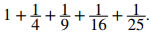
a. Escriba



Regla 5.1_1: Propiedades de la notación sigma
|
Supongamos que a1, a2, …, an y b1, b2, …, bn representan dos secuencias de términos y que c sea una constante. Las siguientes propiedades son válidas para todos los enteros positivos m y n , con 1 ≤ m ≤ n.
|
PruebaAquí probamos las propiedades 2. y 3., y dejamos la prueba de las otras tres propiedades como Ejercicios. 2. Se tiene que 3. Se tiene que |
Algunas fórmulas, para sumatorias encontradas con frecuencia, simplifican aún más el proceso de suma. Estas se muestran en la siguiente tabla, para sumas de los primeros n enteros y para las sumas de las potencias segundas y terceras de los primeros n enteros.
Regla 5.1_2: Sumas de números enteros y sumas de potencias de números enteros


Ejemplo ilustrativo 5.1_2. Evaluación de una suma usando la notación Sigma
Escriba usando notación sigma y evalúe las siguientes sumas:
a. La suma de los términos de la forma (i − 3)² para i = 1, 2, …, 200.
b. La suma de los términos de la forma (i³ − i²) para i = 1, 2, 3, 4, 5, 6.
Solución:
a. Desarrollando el producto notable (i − 3)², podemos dar la expresión como la suma de tres términos:


b. Se utiliza la propiedad de notación sigma iv. y las reglas para la suma de términos cuadrados y la suma de términos de cubos:
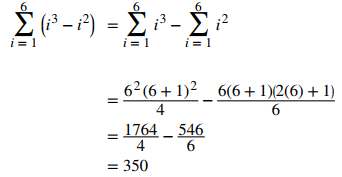
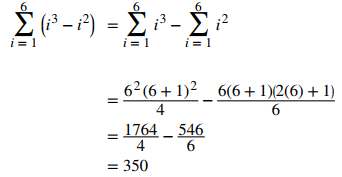
Ejemplo ilustrativo 5.1_3. Encontrar la suma de los valores de una función
Encuentre la suma de los valores de f (x) = x³ para los enteros 1, 2, 3, …, 10.
Solución:
Usando la fórmula respectiva, tenemos


Área aproximada
Ahora que tenemos la notación necesaria, volvemos al problema en cuestión: aproximar el área bajo una curva. Sea f (x) una función continua y no negativa definida en el intervalo cerrado [a, b]. Queremos aproximar el área A delimitada por f (x) arriba, el eje x debajo, la recta x = a a la izquierda y la recta x = b a la derecha (Figura 5.1_1).


¿Cómo aproximamos el área de la región bajo esta curva? El enfoque es geométrico. Al dividir una región en muchas formas pequeñas que tienen fórmulas de área conocidas, podemos sumar estas áreas y obtener una estimación razonable del área real. Comenzamos dividiendo el intervalo [a, b] en n subintervalos de igual ancho, (b − a)/n. Hacemos esto seleccionando puntos igualmente espaciados x0, x1, x2,…, xn con x0 = a, xn = b, y


para i = 1, 2, 3, …, n.
Representamos el ancho de cada subintervalo con la notación Δx, entonces Δx = (b − a)/n y


para i = 1, 2, 3, …, n.
Esta noción de dividir un intervalo [a, b] en subintervalos seleccionando puntos dentro del intervalo se usa con bastante frecuencia para aproximar el área bajo una curva, así que definamos alguna terminología relevante.
Definición 5..1.1. Partición de un intervalo
Un conjunto de puntos P = {xi} para i = 0, 1, 2,…, n con a = x0 < x1 < x2 < ⋯ < xn = b, que divide el intervalo [a, b] en subintervalos de la forma [x0, x1], [x1, x2],…, [xn − 1, xn] se llama una partición de [a, b]. Si todos los subintervalos tienen el mismo ancho, el conjunto de puntos forma una partición regular del intervalo [a, b].
Podemos utilizar este concepto de una partición regular como base de un método para estimar el área bajo la curva. A continuación examinamos dos métodos: la aproximación del punto extremo izquierdo y la aproximación del punto extremo derecho.
Regla 5.1_3: Aproximación de punto extremo izquierdo
En cada subintervalo [xi − 1, xi] (para i = 1, 2, 3,…, n), construya un rectángulo con ancho Δx y altura igual a f (xi − 1), que es el valor de la función en el punto extremo izquierdo del subintervalo. Entonces el área de este rectángulo es f (xi − 1) Δx. Sumando las áreas de todos estos rectángulos, obtenemos un valor aproximado para A (Figura 5.1_2). Usamos la notación Ln para denotar que esta es una aproximación del extremo izquierdo de A usando n subintervalos.


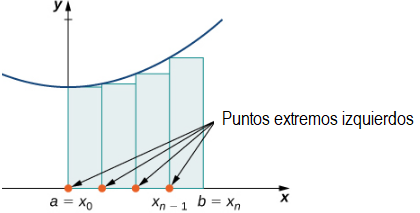

(Figura 5.1_2 En la aproximación del punto extremo izquierdo del área bajo una curva, la altura de cada rectángulo está determinada por el valor de la función en el extremo izquierdo de cada subintervalo.)
El segundo método para aproximar el área bajo una curva es la aproximación del punto extremo derecho. Es casi lo mismo que la aproximación del punto extremo izquierdo, pero ahora las alturas de los rectángulos están determinadas por los valores de la función en el extremo derecho de cada subintervalo.
Regla 5.1_4: Aproximación de punto extremo derecho
Construya un rectángulo en cada subintervalo [xi − 1, xi] (para i = 1, 2, 3,…, n), solo que esta vez la altura del rectángulo está determinada por el valor de la función f (xi) en el punto extremo derecho del subintervalo. Entonces, el área de cada rectángulo es f (xi) Δx y la aproximación para A viene dada por


La notación Rn indica que esta es una aproximación del punto extremo derecho para el área A (Figura 5.1_3).
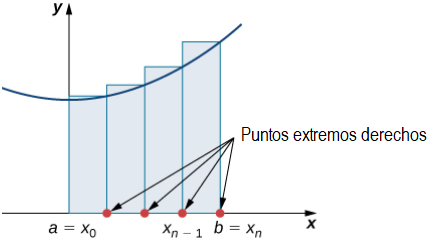

(Figura 5.1_3 En la aproximación del punto extremo derecho del área bajo una curva, la altura de cada rectángulo está determinada por el valor de la función a la derecha de cada subintervalo. Tenga en cuenta que la aproximación del punto final derecho difiere de la aproximación del punto final izquierdo en la Figura 5.1_2.)
Las gráficas en la Figura 5.1_4 representan la curva


En la gráfica (a) dividimos la región representada en el intervalo [0, 3] en seis subintervalos, cada uno de ancho 0.5. Por lo tanto, Δx = 0.5. Luego formamos seis rectángulos dibujando líneas verticales perpendiculares a xi − 1 (el punto extremo izquierdo de cada subintervalo). Determinamos la altura de cada rectángulo calculando f (xi − 1) para i = 1, 2, 3, 4, 5, 6. Los intervalos son [0, 0.5], [0.5, 1], [1, 1.5], [1.5, 2], [2, 2.5], [2.5, 3]. Encontramos el área de cada rectángulo multiplicando la altura por el ancho. Luego, la suma de las áreas rectangulares se aproxima al área entre f (x) y el eje x. Cuando los puntos extremos izquierdos se usan para calcular la altura, tenemos una aproximación del punto extremo izquierdo. Así,




En la figura 5.1_4 (b), dibujamos líneas verticales perpendiculares a xi, de modo que xi es el punto extremo derecho de cada subintervalo, y calculamos f (xi) para i = 1, 2, 3, 4, 5, 6. Multiplicamos cada f (xi) por Δx para encontrar las áreas rectangulares, y luego las sumamos. Esta es una aproximación del punto extremo derecho del área bajo f (x). Así,


Ejemplo ilustrativo 5.1_4. Aproximación del área bajo una curva
Utilice las aproximaciones del punto extremo izquierdo y del punto extremo derecho para aproximar el área bajo la curva de f (x) = x² en el intervalo [0, 2]; use n = 4.
Solución:
Primero, divida el intervalo [0, 2] en n subintervalos iguales. Usando n = 4, Δx = (2−0)/4 = 0.5. Este es el ancho de cada rectángulo. Los intervalos [0, 0.5], [0.5, 1], [1, 1.5], [1.5, 2] se muestran en la Figura 5.1_5. Usando una aproximación del punto extremo izquierdo, las alturas son f (0) = 0, f (0.5) = 0.25, f (1) = 1, f (1.5) = 2.25. Entonces,




La aproximación del punto extremo derecho se muestra en la Figura 5.1_6. Los intervalos son los mismos, Δx = 0.5, pero ahora use el punto extremo derecho para calcular la altura de los rectángulos. Tenemos




La aproximación del punto final izquierdo es 1.75; la aproximación del punto final derecho es 3.75. ◊
De lo anterior nos percatamos que cuando usamos un pequeño número de intervalos, ni la aproximación del punto extremo izquierdo ni la aproximación del punto extremo derecho es una estimación particularmente precisa del área bajo la curva. Sin embargo, parece lógico que si aumentamos el número de puntos en nuestra partición, nuestra estimación del área A mejorará. Tendremos más rectángulos, pero cada rectángulo será más delgado, por lo que podremos ajustar los rectángulos a la curva con mayor precisión.
Podemos observar la aproximación mejorada obtenida con la elección de intervalos cada vez más pequeños con un ejemplo. Exploremos la idea de aumentar n, primero en una aproximación del punto extremo izquierdo con cuatro rectángulos, luego ocho rectángulos y finalmente 32 rectángulos. Luego, hagamos lo mismo en una aproximación del punto extremo derecho, usando los mismos conjuntos de intervalos, para la misma región curva.
La figura 5.1_7 muestra el área de la región bajo la curva


en el intervalo [0, 2] usando una aproximación del punto extremo izquierdo donde n = 4. El ancho de cada rectángulo es


El área de la región se aproxima por la suma de las áreas de los cuatro rectángulos inscritos, o




La figura 5.1_8 muestra la misma curva dividida en ocho subintervalos. Comparando el gráfico con cuatro rectángulos en la Figura 5.1_7 con este gráfico con ocho rectángulos, podemos ver que parece haber menos espacio en blanco debajo de la curva cuando n = 8. Este espacio en blanco es un área debajo de la curva que no podemos incluir usando nuestra aproximación del área de región estudiada. El área de los rectángulos es


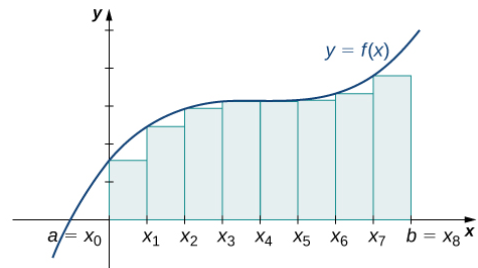

El gráfico de la figura 5.1_9 muestra la misma función con 32 rectángulos inscritos debajo de la curva. Parece que queda poco espacio en blanco. El área ocupada por los rectángulos es




Podemos llevar a cabo un proceso similar para el método de aproximación del punto extremo derecho. Una aproximación del punto extremo derecho de la misma curva, usando cuatro rectángulos, esta vez circunscritos (Figura 5.1_10), produce la siguiente área aproximada de la región




Dividir la región sobre el intervalo [0, 2] en ocho rectángulos da como resultado Δx = (2 − 0)/8 = 0.25. El gráfico se muestra en la Figura 5.1_11. El área es




Por último, la aproximación del punto extremo derecho con n = 32 está más cerca del valor real del área (Figura 5.1_12). El área es aproximadamente




Según estas cifras y cálculos, parece que estamos en el camino correcto; los rectángulos parecen aproximarse mejor al área bajo la curva a medida que n se hace más grande. Además, a medida que n aumenta, las aproximaciones del punto extremo izquierdo y del punto extremo derecho parecen aproximarse a un área de 8 unidades cuadradas. La tabla 5.1_1 muestra una comparación numérica de los métodos de punto extremo izquierdo y derecho. La idea de que las aproximaciones del área bajo la curva mejoran cada vez más a medida que n se hace más y más grande es muy importante, y a continuación exploramos esta idea con más detalle.
| Valores de n | Área aproximada Ln | Área aproximada Rn |
|---|---|---|
| n = 4 | 7.5 | 8.5 |
| n = 8 | 7.75 | 8.25 |
| n = 32 | 7.94 | 8.06 |
(Tabla 5.1_1 Valores convergentes de aproximaciones de punto extremo izquierdo y derecho a medida que n aumenta)
Formando sumas de Riemann
Hasta ahora hemos estado usando rectángulos para aproximar el área bajo una curva. Las alturas de estos rectángulos se han determinado evaluando la función en los puntos extremos derecho o izquierdo del subintervalo [xi − 1, xi]. En realidad, no hay razón para restringir la evaluación de la función a uno de estos dos puntos solamente. Podríamos evaluar la función en cualquier punto xi* en el subintervalo [xi − 1, xi], y usar f (xi*) como la altura de nuestro rectángulo. Esto nos da una estimación del área de la forma


Una suma de esta tipo se llama suma de Riemann, llamada así por el matemático del siglo XIX Bernhard Riemann, quien desarrolló la idea.
Definición 5.1.2. Suma de Riemann
|
Sea f (x) una función definida en un intervalo cerrado [a, b] y sea P una partición regular de [a, b]. Sea Δx el ancho de cada subintervalo [xi − 1, xi] y para cada i, sea xi* cualquier punto en [xi − 1, xi]. Una suma de Riemann se define para f (x) como
Recuerde que con las aproximaciones de punto extremo izquierdo y derecho, las estimaciones parecen mejorar a medida que n se hace más y más grande. Lo mismo sucede con las sumas de Riemann. Las sumas de Riemann dan mejores aproximaciones para valores mayores de n. Ahora estamos listos para definir el área bajo una curva en términos de sumas de Riemann. |
Definición 5.1.3. Área bajo la curva
|
Sea f (x) una función continua y no negativa en un intervalo [a, b], y tal que
sea una suma de Riemann para f (x). Entonces, el área bajo la curva y = f (x) en [a, b] viene dada por
|
Algunas sutilezas aquí vale la pena discutir. Primero, tenga en cuenta que tomar el límite de una suma es un poco diferente de tomar el límite de una función f (x) cuando x va al infinito. Los límites de las sumas se discuten en detalle en el capítulo sobre Sucesiones y Series; sin embargo, por ahora podemos suponer que las técnicas computacionales que usamos para calcular los límites de las funciones también se pueden usar para calcular los límites de las sumas.
En segundo lugar, debemos considerar qué hacer si la expresión converge a límites diferentes para diferentes opciones de {xi*}. Afortunadamente, esto no sucede. Aunque la prueba está más allá del alcance de este texto, se puede demostrar que si f (x) es continua en el intervalo cerrado [a, b], entonces


existe y es único (en otras palabras, no depende de la elección de {xi*}.
Veremos algunos ejemplos en breve. Pero, antes de hacerlo, tomémonos un momento y hablemos sobre algunas opciones específicas para {xi*}.
Aunque cualquier opción para {xi*} nos da una estimación del área bajo la curva, no sabemos necesariamente si esa estimación es demasiado alta (sobreestimada) o demasiado baja (subestimada). Si es importante saber si nuestra estimación es alta o baja, podemos seleccionar nuestro valor para {xi*} para garantizar un resultado u otro.
Si queremos una sobreestimación, por ejemplo, podemos elegir {xi*} de modo que para i = 1, 2, 3, …, n, f ({xi*}) ≥ f (x) para todos x ∈ [xi − 1, xi]. En otras palabras, elegimos {xi*} para que, con i = 1, 2,3 , …, n, f {xi*} sea el valor máximo de la función en el intervalo [xi − 1, xi]. Si seleccionamos {xi*} de esta manera, entonces la suma de Riemann
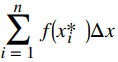
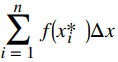
se llama una suma superior.
Del mismo modo, si queremos una subestimación, podemos elegir {xi*} para que, con i = 1, 2, 3, …, n, f (xi*) sea el valor mínimo de la función en el intervalo [xi − 1, xi]. En este caso, la suma de Riemann asociada se denomina suma inferior. Tenga en cuenta que si f (x) crece o decrece a lo largo de todo el intervalo [a, b], entonces los valores máximos y mínimos de la función se producen en los puntos extremos de los subintervalos, por lo que, en este caso, las sumas superior e inferior son iguales a las aproximaciones de punto extremo izquierdo y derecho.
Ejemplo ilustrativo 5.1_5. Encontrar sumas inferiores y superiores
Encuentre una suma inferior para f (x) = 10 − x² en [1, 2]; tome n = 4 subintervalos.
Solución:
Con n = 4 en el intervalo [1, 2], Δx = 1/4. Podemos enumerar los intervalos como [1, 1.25], [1.25, 1.5], [1.5, 1.75], [1.75, 2]. Debido a que la función está decreciendo en el intervalo [1, 2], la Figura 5.1_13 muestra que se obtiene una suma inferior utilizando los puntos finales derechos.


La suma de Riemann es


El área de 7.28 es una suma inferior y una subestimación. ◊
Ejemplo ilustrativo 5.1_6. Encontrar sumas inferiores y superiores para f (x) = senx
Encuentre una suma inferior para f (x) = senx durante el intervalo [a, b] = [0, π/2]; tomar n = 6.
Solución:
Primero veamos el gráfico en la Figura 5.1_14 para tener una mejor idea del área de interés.


Los intervalos son [0, π/12], [π/12, π/6], [π/6, π/4], [π/4, π/3], [π/3, 5π/12] y [5π/12, π/2]. Tenga en cuenta que f (x) = senx crece en el intervalo [0, π/2], por lo que una aproximación del punto extremo izquierdo nos da la suma inferior. Una aproximación del punto extremo izquierdo es la suma de Riemann


Tenemos que:
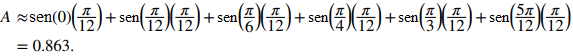
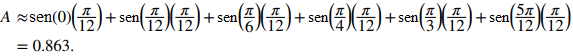

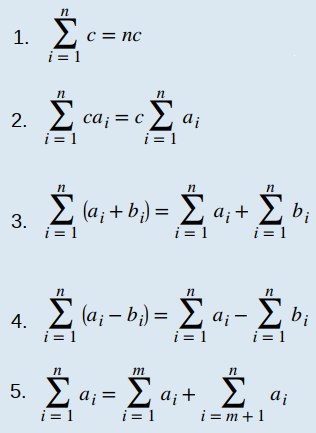

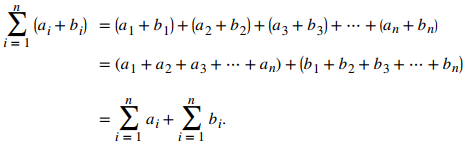
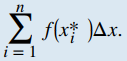

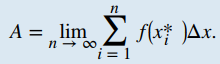
Hola!
Bienvenido! 👀👍😺