| 4. Aplicaciones de la derivada | Ejercicios propuestos para el Capítulo 4.10 |

4.10. ANTIDERIVADAS

Objetivos de aprendizaje:

4.10.1. Encontrar la antiderivada general de una función dada.
4.10.2. Explicar los términos y la notación utilizados para una integral indefinida.
4.10.3. Indicar la regla de la potencia para integrales.
4.10.4. Usar la antidiferenciación para resolver problemas simples de valor inicial.

    En este punto, hemos visto cómo calcular derivadas de muchas funciones y se nos ha presentado una variedad de sus aplicaciones. Ahora hacemos una pregunta que da vuelta a este proceso: Dada una función f, ¿cómo encontramos una función con la derivada f y por qué estaríamos interesados en tal función?

Respondemos la primera parte de esta pregunta definiendo Antiderivadas. La antiderivada de una función f es una función con una derivada f. ¿Por qué nos interesan las antiderivadas? La necesidad de antiderivadas surge en muchas situaciones, y observaremos varios ejemplos en el resto del texto. Aquí examinamos un ejemplo específico que involucra movimiento rectilíneo.

En nuestro examen en Derivadas del movimiento rectilíneo, mostramos que dada una función de posición s(t) de un objeto, entonces su función de velocidad v(t) es la derivada de s(t), es decir, v(t) = s′(t). Además, la aceleración a(t) es la derivada de la velocidad v(t), es decir, a(t)  = v′(t) = s″(t). Ahora supongamos que se nos da una función de aceleración a, pero no la función de velocidad v o la función de posición s. Como a(t) = v′(t), determinar la función de velocidad requiere que encontremos una antiderivada de la función de aceleración. Entonces, dado que v(t) = s′(t), determinar la función de posición requiere que encontremos una antiderivada de la función de velocidad. El movimiento rectilíneo es solo un caso en el que surge la necesidad de antiderivadas. Veremos muchos más ejemplos en el resto del texto. Por ahora, veamos la terminología y la notación de las antiderivadas, y determinemos las antiderivadas para varios tipos de funciones. Examinamos varias técnicas para encontrar antiderivadas de funciones más complicadas más adelante en el texto (en Introducción a las técnicas de integración).

El reverso de la diferenciación

En este punto, sabemos cómo encontrar derivadas de varias funciones. Ahora hacemos la pregunta opuesta. Dada una función f, ¿cómo podemos encontrar una función con la derivada f ? Si podemos encontrar una función F con derivada f, llamamos a F una antiderivada de f.

Definición 4.10.1. Antiderivada

Una función F es una antiderivada de la función f si

F ′(x) = f (x) 

para todo x en el dominio de f. ♦

Considere la función f (x) = 2x. Conociendo la regla de la potencia de diferenciación, concluimos que

F (x) = x²

es una antiderivada de f ya que F ′(x) = 2x. ¿Hay otras antiderivadas de f ?: si; Como la derivada de cualquier constante C es cero,

F (x) = x² + C

también es una antiderivada de f (x) = 2x. Por lo tanto, F (x) = x² + 5 y F (x) = x² − √2 también son antiderivadas de f (x) = 2x.

¿Hay otras antiderivadas de f (x) = 2x  que no sean de la forma x² + C para alguna constante C ? La respuesta es no. Por el Corolario 2 del Teorema del valor medio, sabemos que si F y G son funciones diferenciables tales que F ′(x) = G′(x), entonces F(x) − G(x) = C para alguna constante C. Este hecho lleva al siguiente teorema importante.

Teorema 4.10.1.  Forma general de una antiderivada

Sea F una antiderivada de f en un intervalo I. Entonces, para cada constante C, la función F(x) + C también es una antiderivada de f sobre I; si G es una antiderivada de f sobre I, hay una constante C para la cual G(x) = F(x) + C sobre I. En otras palabras, la forma más general de la antiderivada de f sobre I es F(x) + C.

Usamos este hecho y nuestro conocimiento de las derivadas para encontrar todas las antiderivadas para varias funciones.

Ejemplo ilustrativo 4.10.1: Encontrando antiderivadas

Para cada una de las siguientes funciones, encuentre todas las antiderivadas:

a. \( f(x) = 3x^2 \)

b. \( f(x) = \frac{1}{x} \)

c. \( f(x) = \cos x \)

d. \( f(x) = e^x \)

Solución:

a. Porque

\( \frac{d}{dx}(x^3) = 3x^2 \)

entonces \( F(x) = x^3 \) es una antiderivada de \( 3x^2 \). Por lo tanto, cada antiderivada de \( 3x^2 \) es de la forma \( x^3 + C \) para alguna constante \( C \), y cada función de la forma \( x^3 + C \) es una antiderivada de \( 3x^2 \).

b. Sea \( f(x) = \ln |x| \). Para \( x > 0 \), \( f(x) = \ln(x) \) y

\( \frac{d}{dx}(\ln x) = \frac{1}{x} \).

Para \( x < 0 \), \( f(x) = \ln(-x) \) y

\( \frac{d}{dx}(\ln(-x)) = -\frac{1}{-x} = \frac{1}{x} \).

Por lo tanto,

\( \frac{d}{dx}(\ln|x|) = \frac{1}{x} \).

Así, \( F(x) = \ln |x| \) es una antiderivada de \( \frac{1}{x} \). Por lo tanto, cada antiderivada de \( \frac{1}{x} \) es de la forma \( \ln |x| + C \) para alguna constante \( C \) y cada función de la forma \( \ln |x| + C \) es una antiderivada de \( \frac{1}{x} \).

c. Tenemos

\( \frac{d}{dx}(\sin x) = \cos x, \)

así que \( F(x) = \sin x \) es una antiderivada de \( \cos x \). Por lo tanto, cada antiderivada de \( \cos x \) es de la forma \( \sin x + C \) para alguna constante \( C \), y cada función de la forma \( \sin x + C \) es una antiderivada de \( \cos x \).

d. Dado que

\( \frac{d}{dx}(e^x) = e^x, \)

entonces \( F(x) = e^x \) es una antiderivada de \( e^x \). Por lo tanto, cada antiderivada de \( e^x \) es de la forma \( e^x + C \) para alguna constante \( C \) y toda función de la forma \( e^x + C \) es una antiderivada de \( e^x \). ♦

Ejercicio de control 4.10.1

Encuentra todas las antiderivadas de f (x) = sen x. ♦

Integrales indefinidas

Ahora damos la notación formal utilizada para representar las antiderivadas y examinamos algunas de sus propiedades. Estas propiedades nos permiten encontrar antiderivadas de funciones más complicadas. Dada una función f, usamos la notación f ′(x) o df/dx para denotar la derivada de f. Ahora presentamos la notación para antiderivadas. Si F es una antiderivada de f, decimos que F(x) + C es la antiderivada más general de f  y escribimos

El símbolo ∫ se llama signo integral, y ∫ f (x) dx se llama integral indefinida de f.

 

Definición 4.10.2. Integral indefinida

Dada una función f, la integral indefinida de f, denotada

es la antiderivada más general de f. Si F es una antiderivada de f, entonces

La expresión f (x) se llama integrando y la variable x es la variable de integración. ♦

        Dada la terminología introducida en esta definición, el acto de encontrar las antiderivadas de una función f generalmente se conoce como integración f.

Para una función f y una antiderivada F, las funciones F(x) + C, donde C es cualquier número real, a menudo se refieren como la familia de antiderivadas de f.

Por ejemplo, dado que x² es una antiderivada de 2x y cualquier antiderivada de 2x tiene la forma x² + C, escribimos

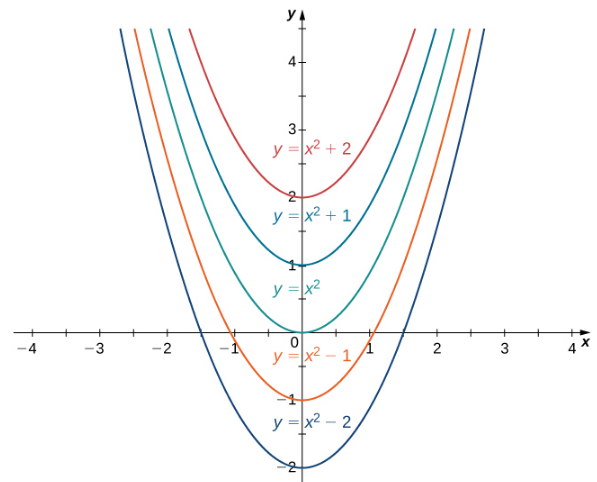
La colección de todas las funciones de la forma x² + C, donde C es cualquier número real, se conoce como la familia de antiderivadas de 2x. La figura 4.10_1 muestra las gráficas de algunos miembros de esta familia de Antiderivadas.

Para algunas funciones, la evaluación de integrales indefinidas se sigue directamente de las propiedades de los derivados. Por ejemplo, para n ≠ −1,

que viene directamente de

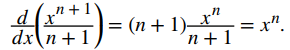
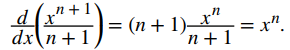
Este hecho se conoce como la regla de la potencia para integrales.

Teorema 4.10.2. Regla de la potencia para integrales

Para n ≠ −1,

\( \int x^n \, dx = \dfrac{x^{n+1}}{n+1} + C. \)

♦

Tabla de integrales para algunas funciones comunes

La evaluación de integrales indefinidas para algunas otras funciones también es un cálculo sencillo. La siguiente tabla enumera las integrales indefinidas para varias funciones comunes.:

Fórmula de Derivación	Integral Indefinida
\( \frac{d}{dx}(k) = 0 \)	\( \int k \, dx = kx^0 \, dx = kx + C \)
\( \frac{d}{dx}(x^n) = nx^{n-1} \)	\( \int x^n \, dx = \frac{x^{n+1}}{n+1} + C \text{ para } n \neq -1 \)
\( \frac{d}{dx}(\ln |x|) = \frac{1}{x} \)	\( \int \frac{1}{x} \, dx = \ln|x| + C \)
\( \frac{d}{dx}(e^x) = e^x \)	\( \int e^x \, dx = e^x + C \)
\( \frac{d}{dx}(\sin x) = \cos x \)	\( \int \cos x \, dx = \sin x + C \)
\( \frac{d}{dx}(\cos x) = – \sin x \)	\( \int \sin x \, dx = – \cos x + C \)
\( \frac{d}{dx}(\tan x) = \sec^2 x \)	\( \int \sec^2 x \, dx = \tan x + C \)
\( \frac{d}{dx}(\csc x) = – \csc x \cot x \)	\( \int \csc x \cot x \, dx = – \csc x + C \)
\( \frac{d}{dx}(\sec x) = \sec x \tan x \)	\( \int \sec x \tan x \, dx = \sec x + C \)
\( \frac{d}{dx}(\cot x) = – \csc^2 x \)	\( \int \csc^2 x \, dx = – \cot x + C \)
\( \frac{d}{dx}(\sin^{-1} x) = \frac{1}{\sqrt{1-x^2}} \)	\( \int \frac{1}{\sqrt{1-x^2}} \, dx = \sin^{-1} x + C \)
\( \frac{d}{dx}(\tan^{-1} x) = \frac{1}{1+x^2} \)	\( \int \frac{1}{1+x^2} \, dx = \tan^{-1} x + C \)
\( \frac{d}{dx}(\sec^{-1}|x|) = \frac{1}{x\sqrt{x^2 – 1}} \)	\( \int \frac{1}{x \sqrt{x^2-1}} \, dx = \sec^{-1} |x| + C \)

Tabla 4.10.1 Fórmulas de Integración

De la definición de integral indefinida de f, sabemos que

si y sólo si F es una antiderivada de f. Por lo tanto, al afirmar que

Es importante verificar si esta afirmación es correcta mostrando que F ′ (x) = f (x).

Ejemplo ilustrativo 4.10.2: Verificando una integral indefinida

Cada una de las siguientes afirmaciones es de la forma \( \int f(x) \, dx = F(x) + C \). Verifique que cada afirmación es correcta mostrando que \( F'(x) = f(x) \).

1. \( \int (x + e^x) \, dx = \frac{x^2}{2} + e^x + C \)
2. \( \int x e^x \, dx = xe^x – e^x + C \)

Solución:

a. Dado que

\( \frac{d}{dx}\left(\frac{x^2}{2} + e^x + C\right) = x + e^x \),

la afirmación

\( \int (x + e^x) \, dx = \frac{x^2}{2} + e^x + C \)

es correcta. Tenga en cuenta que estamos verificando una integral indefinida para una suma. Además, \( \frac{x^2}{2} \) y \( e^x \) son antiderivadas de \( x \) y \( e^x \), respectivamente, y la suma de las antiderivadas es una antiderivada de la suma. Discutimos este hecho nuevamente más adelante en esta sección.

b. Usando la regla del producto, vemos que

\( \frac{d}{dx}(xe^x – e^x + C) = e^x + xe^x – e^x = xe^x. \)

Por lo tanto, la afirmación

\( \int x e^x \, dx = xe^x – e^x + C \)

es correcta. Observe que estamos verificando una integral indefinida para un producto. La antiderivada \( xe^x – e^x \) no es un producto de las antiderivadas. Además, el producto de las antiderivadas, \( \frac{x^2 e^x}{2} \) no es una antiderivada de \( xe^x \) ya que

\( \frac{d}{dx} \left(\frac{x^2 e^x}{2}\right) = xe^x + \frac{x^2 e^x}{2} \neq xe^x \).

En general, el producto de antiderivadas no es una antiderivada de un producto. ♦

Ejercicio de control 4.10.2

Verifique que \( \int x \cos x \, dx = x \sin x + \cos x + C \). ♦

Propiedades algebraicas de las integrales indefinidas

En Tabla 4.10.1, enumeramos las integrales indefinidas para muchas funciones elementales. Ahora centremos nuestra atención en evaluar integrales indefinidas para funciones más complicadas. Por ejemplo, considere encontrar una antiderivada de una suma \( f + g \). En el Ejemplo 4.10.2a, mostramos que una antiderivada de la suma \( x + e^x \) está dada por la suma \( \left( \frac{x^2}{2} \right) + e^x \) —es decir, una antiderivada de una suma está dada por una suma de antiderivadas. Este resultado no fue específico para este ejemplo. En general, si \( F \) y \( G \) son antiderivadas de cualesquiera funciones \( f \) y \( g \), respectivamente, entonces

\( \frac{d}{dx}(F(x) + G(x)) = F'(x) + G'(x) = f(x) + g(x). \)

Por lo tanto, \( F(x) + G(x) \) es una antiderivada de \( f(x) + g(x) \) y tenemos

\( \int (f(x) + g(x)) \, dx = F(x) + G(x) + C. \)

Similarmente,

\( \int (f(x) – g(x)) \, dx = F(x) – G(x) + C. \)

Además, considere la tarea de encontrar una antiderivada de \( kf(x) \), donde \( k \) es cualquier número real. Dado que

\( \frac{d}{dx}(kf(x)) = k \frac{d}{dx}F(x) = kf'(x) \)

para cualquier número real \( k \), concluimos que

\( \int kf(x) \, dx = kF(x) + C. \)

Estas propiedades se resumen a continuación.

Teorema 4.10.3. Propiedades de las integrales indefinidas

Sean \( F \) y \( G \) antiderivadas de \( f \) y \( g \), respectivamente, y sea \( k \) cualquier número real.

Sumas y Diferencias

\( \int (f(x) \pm g(x)) \, dx = F(x) \pm G(x) + C \)

Múltiplos Constantes

\( \int kf(x) \, dx = kF(x) + C \)

♦

A partir de este teorema, podemos evaluar cualquier integral que implique una suma, diferencia o múltiplo constante de funciones con antiderivadas conocidas. Evaluar integrales que involucran productos, cocientes o composiciones es más complicado. Observamos y abordamos integrales que involucran estas funciones más complicadas en Introducción a la integración.

Ejemplo ilustrativo 4.10.3: Evaluando integrales indefinidas

Evaluar cada una de las siguientes integrales indefinidas:

1. \( \int (5x^3 – 7x^2 + 3x + 4) \, dx \)
2. \( \int \frac{x^2 + 4\sqrt[3]{x}}{x} \, dx \)
3. \( \int \frac{4}{1 + x^2} \, dx \)
4. \( \int \tan x \cos x \, dx \)

Solución:

a. Usando Propiedades de las Integrales Indefinidas, podemos integrar cada uno de los cuatro términos en el integrando por separado. Obtenemos

\( \int (5x^3 – 7x^2 + 3x + 4) \, dx = \int 5x^3 \, dx – \int 7x^2 \, dx + \int 3x \, dx + \int 4 \, dx. \)

De la segunda parte de Propiedades de las Integrales Indefinidas, cada coeficiente se puede escribir delante del signo integral, lo que da

\( \int 5x^3 \, dx – \int 7x^2 \, dx + \int 3x \, dx + \int 4 \, dx = 5 \int x^3 \, dx – 7 \int x^2 \, dx + 3 \int x \, dx + 4 \int 1 \, dx. \)

Usando la regla de la potencia para integrales, concluimos que

\( \int (5x^3 – 7x^2 + 3x + 4) \, dx = \frac{5}{4}x^4 – \frac{7}{3}x^3 + \frac{3}{2}x^2 + 4x + C. \)

b. Reescriba el integrando como

\( \frac{x^2 + 4 \sqrt[3]{x}}{x} = \frac{x^2}{x} + \frac{4 \sqrt[3]{x}}{x}. \)

Luego, para evaluar la integral, integre cada uno de estos términos por separado. Usando la regla de la potencia, tenemos

\( \int \left(x + \frac{4}{x^{2/3}}\right) \, dx = \int x \, dx + 4 \int x^{-2/3} \, dx = \frac{1}{2}x^2 + 4 \frac{1}{\left(-\frac{2}{3}\right) + 1} x^{\left(-\frac{2}{3}\right) + 1} + C = \frac{1}{2}x^2 + 12x^{1/3} + C. \)

c. Usando Propiedades de las Integrales Indefinidas, escriba la integral como

\( 4 \int \frac{1}{1+x^2} \, dx. \)

Luego, use el hecho de que \( \tan^{-1}(x) \) es una antiderivada de \( \frac{1}{1+x^2} \) para concluir que

\( \int \frac{4}{1+x^2} \, dx = 4 \tan^{-1}(x) + C. \)

d. Reescriba el integrando como

\( \tan x \cos x = \frac{\sin x}{\cos x} \cos x = \sin x. \)

Por lo tanto,

\( \int \tan x \cos x \, dx = \int \sin x \, dx = – \cos x + C. \)

♦

Ejercicio de control 4.10.3

Evaluar \( \int (4x^3 – 5x^2 + x – 7) \, dx \). ♦

Problemas de valor inicial

Observamos técnicas para integrar una gran variedad de funciones que involucran productos, cocientes y composiciones más adelante en el texto. Aquí pasamos a un uso común para los antiderivadas que surge a menudo en muchas aplicaciones: resolver ecuaciones diferenciales.

Una ecuación diferencial es una ecuación que relaciona una función desconocida y una o más de sus derivadas. La ecuación

es un ejemplo simple de una ecuación diferencial. Resolver esta ecuación significa encontrar una función y cuya primera derivada sea igual a f(x). Por lo tanto, las soluciones de esta ecuación son las antiderivadas de f. Si F es una antiderivada de f, cada función de la forma y = F (x) + C es una solución de esa ecuación diferencial. Por ejemplo, las soluciones de

son dadas por

A veces estamos interesados en determinar si una curva de solución particular pasa por un cierto punto (x₀, y₀), es decir, y(x₀) = y₀. El problema de encontrar una función y que satisfaga una ecuación diferencial

con la condición adicional

es un ejemplo de un problema de valor inicial. La condición y(x₀) = y₀ se conoce como condición inicial.

Por ejemplo, buscando una función y que satisfaga la ecuación diferencial

y la condición inicial

es un ejemplo de un problema de valor inicial. Dado que las soluciones de la ecuación diferencial son

para encontrar una función y que también satisfaga la condición inicial, necesitamos encontrar C tal que

A partir de esta ecuación, vemos que C = 3, y concluimos que

es la solución de este problema de valor inicial como se muestra en la siguiente gráfica.

Ejemplo ilustrativo 4.10.4: Resolviendo un problema de valor inicial

Resuelva el problema de valor inicial

\( \frac{dy}{dx} = \sin x, \quad y(0) = 5. \)

Solución:

Primero necesitamos resolver la ecuación diferencial. Si \( \frac{dy}{dx} = \sin x \), entonces

\( y = \int \sin(x) \, dx = -\cos x + C. \)

Luego necesitamos buscar una solución \( y \) que satisfaga la condición inicial. La condición inicial \( y(0) = 5 \) significa que necesitamos una constante \( C \) tal que \( -\cos x + C = 5 \). Por lo tanto,

\( C = 5 + \cos(0) = 6. \)

La solución del problema de valor inicial es \( y = -\cos x + 6 \). ♦

Ejercicio de control 4.10.4

Resuelva el problema de valor inicial \( \frac{dy}{dx} = 3x^{-2}, y(1) = 2 \). ♦

      Los problemas de valor inicial surgen en muchas aplicaciones. A continuación, consideramos un problema en el que un conductor aplica los frenos en un automóvil. Nos interesa saber cuánto tiempo tarda el coche en detenerse. Recordemos que la función de velocidad v(t) es la derivada de una función de posición s(t), y la aceleración a(t) es la derivada de la función de velocidad. En ejemplos anteriores del texto, podíamos calcular la velocidad a partir de la posición y luego calcular la aceleración a partir de la velocidad. En el siguiente ejemplo trabajamos al revés. Dada una función de aceleración, calculamos la función de velocidad. Luego, usamos la función de velocidad para determinar la función de posición.

Ejemplo ilustrativo 4.10.5: Coche desacelerando

Un automóvil viaja a una velocidad de 88 pies/seg (60 mph) cuando se aplican los frenos. El automóvil comienza a desacelerar a una velocidad constante de 15 pies/seg².

1. ¿Cuántos segundos transcurren antes de que el automóvil se detenga?
2. ¿Qué tan lejos viaja el automóvil durante ese tiempo?

Solución:

a. Primero introducimos variables para este problema. Sea \( t \) el tiempo (en segundos) después de que se aplican los frenos por primera vez. Sea \( a(t) \) la aceleración del automóvil (en pies por segundo al cuadrado) en el tiempo \( t \). Sea \( v(t) \) la velocidad del automóvil (en pies por segundo) en el tiempo \( t \). Sea \( s(t) \) la posición del automóvil (en pies) más allá del punto donde se aplican los frenos en el tiempo \( t \).

El automóvil viaja a una velocidad de 88 pies/seg. Por lo tanto, la velocidad inicial es \( v(0) = 88 \) pies/seg. Dado que el automóvil está desacelerando, la aceleración es

\( a(t) = -15 \text{ pies/seg}^2. \)

La aceleración es la derivada de la velocidad,

\( v'(t) = -15. \)

Por lo tanto, tenemos un problema de valor inicial para resolver:

\( v'(t) = -15, \quad v(0) = 88. \)

Integrando, encontramos que

\( v(t) = -15t + C. \)

Dado que \( v(0) = 88 \), \( C = 88 \). Por lo tanto, la función de velocidad es

\( v(t) = -15t + 88. \)

Para encontrar cuánto tiempo tarda el automóvil en detenerse, necesitamos encontrar el tiempo \( t \) tal que la velocidad sea cero. Resolviendo \( -15t + 88 = 0 \), obtenemos \( t = \frac{88}{15} \) seg.

b. Para encontrar qué tan lejos viaja el automóvil durante este tiempo, necesitamos encontrar la posición del automóvil después de \( \frac{88}{15} \) seg. Sabemos que la velocidad \( v(t) \) es la derivada de la posición \( s(t) \). Considere la posición inicial como \( s(0) = 0 \). Por lo tanto, necesitamos resolver el problema de valor inicial

\( s'(t) = -15t + 88, \quad s(0) = 0. \)

Integrando, tenemos

\( s(t) = -\frac{15}{2}t^2 + 88t + C. \)

Dado que \( s(0) = 0 \), la constante es \( C = 0 \). Por lo tanto, la función de posición es

\( s(t) = -\frac{15}{2}t^2 + 88t. \)

Después de \( t = \frac{88}{15} \) seg, la posición es \( s\left(\frac{88}{15}\right) \approx 258.133 \) pies. ♦

Ejercicio de control 4.10.5

Supongamos que el coche viaja a una velocidad de 44 pies/segundo. ¿Cuánto tiempo tarda el coche en detenerse? ¿Qué distancia recorrerá el coche? ♦