1. Funciones y sus gráficas

En los últimos años, se han producido grandes terremotos en varios países del mundo. En enero de 2010, un terremoto de magnitud 7.3 golpeó a Haití. Un terremoto de magnitud 9 sacudió el noreste de Japón en marzo de 2011. En abril de 2014, un terremoto de magnitud 8,2 sacudió la costa del norte de Chile. Que significan estos números? En particular, ¿cómo se compara un terremoto de magnitud 9 con un terremoto de magnitud 8.2? o 7.3? Más adelante en este capítulo, mostramos cómo se utilizan las funciones logarítmicas para comparar la intensidad relativa de dos terremotos en función de la magnitud de cada terremoto (ver Ejemplo 1.5_7).
El cálculo es la matemática que describe los cambios en las funciones. En este capítulo, revisamos todas las funciones necesarias para estudiar el cálculo. Definimos funciones polinómicas, racionales, trigonométricas, exponenciales y logarítmicas. Revisamos cómo evaluar estas funciones y mostramos las propiedades de sus gráficas. Proporcionamos ejemplos de ecuaciones con términos que involucran estas funciones e ilustramos las técnicas algebraicas necesarias para resolverlas. En resumen, este capítulo proporciona la base para el material por venir. Es esencial estar familiarizado y cómodo con estas ideas antes de proceder a la introducción formal del cálculo en el próximo capítulo.
Ejercicios resueltos sobre funciones
Cálculo de Zill
Capítulo 1: Funciones
Capítulo 1.1: Funciones y gráficas
😺 Nota: Pulse sobre el ejercicio requerido para que observe la solución que se da en imagen o en video. 👀
Zill 1.1_1 a 6 En los problemas 1–6, encuentre los valores funcionales indicados:
Zill 1.1_7 y 8 En los ejercicios 7 y 8, encuentre
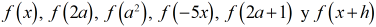
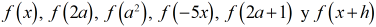
Zill 1.1_9 ¿Para qué valores de x, f (x) = 6x² − 1 es igual a 23?
Zill 1.1_10 ¿Para qué valores de x, f (x) = √(x − 4) es igual a 4?
Zill 1.1_11 a 26 En cada uno de los problemas 11–26, encuentre el dominio de la función f dada:
Zill 1.2_1 a 6 En los problemas 1– 6, encuentre f + g, f −g, f⋅g y f /g:
Soluciones en imagen de ejercicios del tema de funciones


Solución – Juan Beltrán:
f ( x ) = –2 x ² + x ( 1 )
Para hallar los valores funcionales respectivos, se sustituye el valor numérico de la variable independiente x en la fórmula de la función dada en (1), se efectúan las operaciones aritméticas indicadas, se reduce y se simplifica




Solución – Juan Beltrán:


Para hallar los valores funcionales respectivos, se sustituye el valor numérico de la variable independiente x en la fórmula de la función dada en (1), se efectúan las operaciones aritméticas indicadas, se reduce y se simplifica:


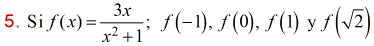
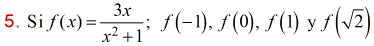
Solución – Juan Beltrán:


Para hallar los valores funcionales respectivos, se sustituye el valor numérico de la variable independiente x en la fórmula de la función dada en (1), se efectúan las operaciones aritméticas indicadas, se reduce y se simplifica:




Solución – Juan Beltrán:


Para hallar los valores funcionales respectivos, se sustituye el valor numérico de la variable independiente x en la fórmula de la función dada en (1), se efectúan las operaciones aritméticas indicadas, se reduce y se simplifica:
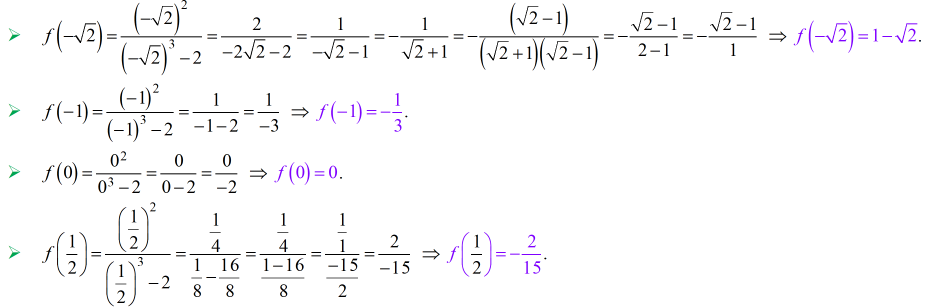
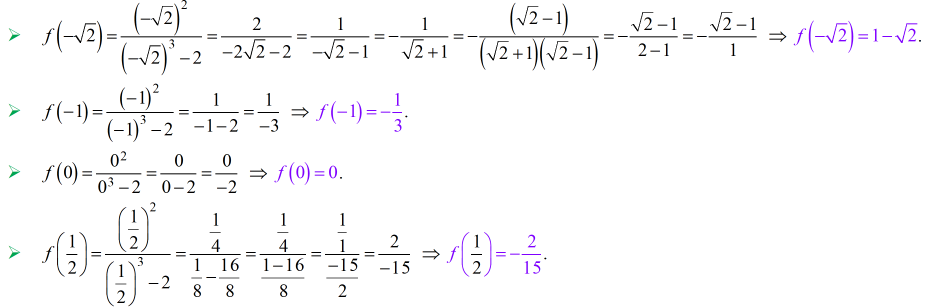


Solución – Juan Beltrán:


Zill 1.1_10 ¿ Para qué valores de x, f (x) = √(x − 4) es igual a 4?
Solución – Juan Beltrán:
Se debe resolver la siguiente ecuación




Solución – Juan Beltrán:
Debido a que las raíces cuadradas de números negativos no son números reales, debemos resolver la siguiente inecuación:




Solución – Juan Beltrán:
Debido a que las raíces cuadradas de números negativos no existen en los reales, debemos resolver la siguiente inecuación:




Solución – Juan Beltrán:
Debido a que las raíces cuadradas de números negativos no existen en los reales y que la división por 0 no tiene sentido, la fórmula que involucra la variable independiente x debe cumplir las siguientes dos condiciones:


que se resumen en esta única condición:
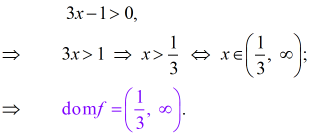
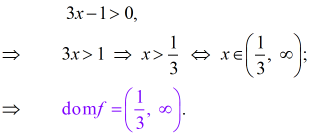


Solución – Juan Beltrán:
Para evitar la división por cero se debe satisfacer la siguiente condición:




Solución – Juan Beltrán:
Para evitar la división por cero se debe satisfacer la siguiente condición:


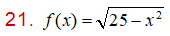
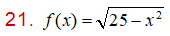
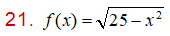
Solución – Juan Beltrán:
Debido a que el dominio de esta función real es un subconjunto de los números reales y teniendo presente que las raíces cuadradas de números negativos no son números reales, debemos resolver la siguiente inecuación


Hay dos posibilidades (de acuerdo con la “ley de los signos”)


ó bien


De tal modo que
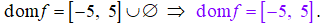
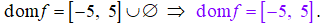



Solución – Juan Beltrán:
Debido a que el dominio de esta función real es un subconjunto de los números reales y teniendo presente que las raíces cuadradas de números negativos no son números reales, debemos resolver la siguiente inecuación


Hay dos posibilidades (de acuerdo con la “ley de los signos”)
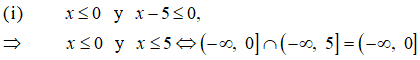
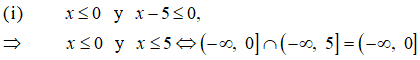
ó bien
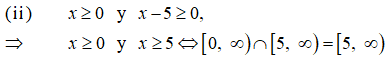
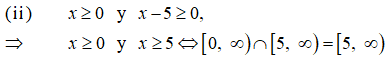
De tal modo que


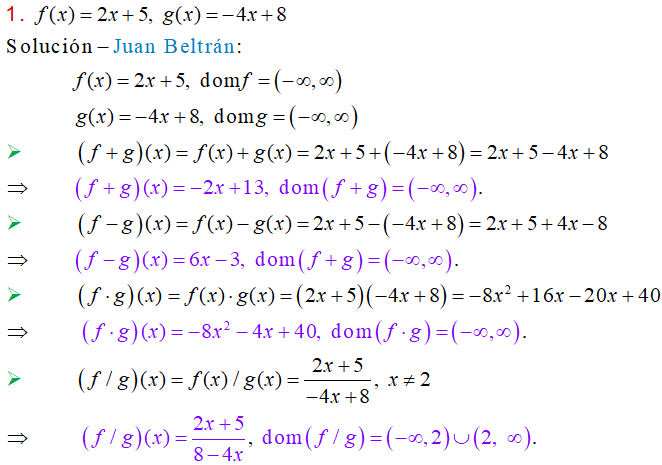
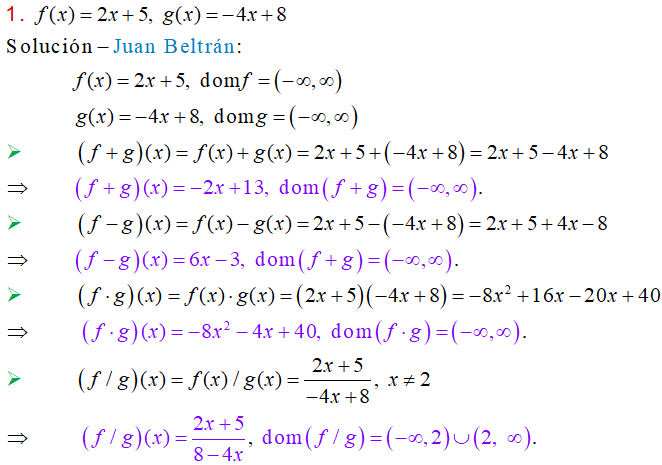


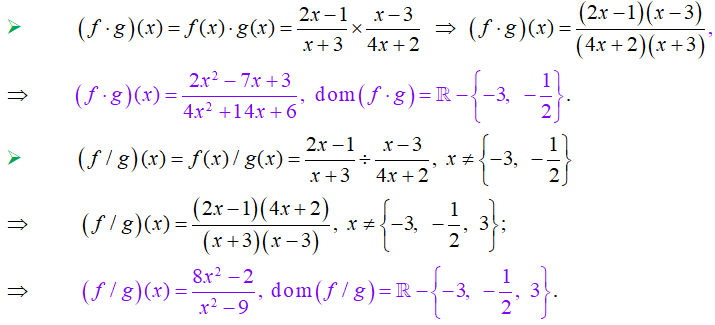
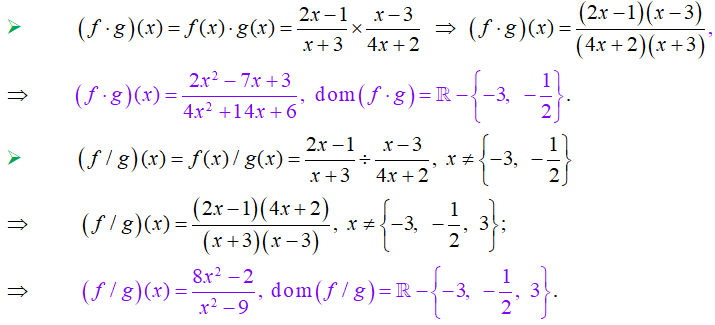
Miscelánea de ejercicios resueltos del capítulo 1
1. (Zill 1.1_1, 4, 8, 9, 13, 18, 23 y 25) Funciones y sus gráficas
2. (Leithold 1.1.1) Determine si el conjunto es una función. Si es una función determine su dominio.
3. (Leithold 1.1.35) Dibuje la gráfica de la función y determine el dominio y el rango (contradominio)


4. (Demidovich 7) La función f (x) es lineal. Hallar dicha función si f (-1) = 2 y f (2) = 3.
(Demidovich 8) Hallar la función de segundo grado f (x) si f (0) = 1, f (1) = 0 y f (3) = 5.
(Demidovich 10) Escribir una sola fórmula que exprese

5. (Demidovich 11 a 14) Determinar el campo de existencia de las funciones dadas:

6. (Demidovich 15 a 17) Determinar el campo de existencia de las funciones dadas: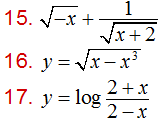
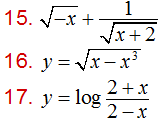










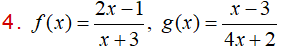
excelente muy bueno para aprender calculo multivariable
Excelente profe mis mas sinceras felicitaciones para que mas.
muy buen aporte profesor
Hola Carlos. Con mucho gusto. Gracias por el comentario! 👍🏻👀
👀😺👍🏻