| 3. La derivada | Ejercicios propuestos para el Capítulo 3.4 |

3.4 Las Derivadas como Tasas de Cambio

Objetivos de aprendizaje:

3.4.1. Determinar un nuevo valor de una cantidad a partir del valor anterior y la cantidad de cambio.
3.4.2. Calcular la tasa de cambio promedio y comprender cómo difiere de la tasa de cambio instantánea.
3.4.3. Aplicar tasas de cambio al desplazamiento, la velocidad y la aceleración de un objeto que se mueve en línea recta.
3.4.4 Predecir la población futura a partir del valor presente y la tasa de crecimiento de la población.
3.4.5. Usar derivadas para calcular el costo marginal y los ingresos en una situación comercial.

    En esta sección veremos algunas aplicaciones de la derivada enfocándonos en la interpretación de la derivada como la tasa de cambio de una función. Estas aplicaciones incluyen aceleración y velocidad en física, tasas de crecimiento de la población en biología y funciones marginales en economía.

Cantidad de cambio de una función

Una aplicación de las derivadas es estimar un valor desconocido de una función en un punto mediante el uso de un valor conocido de la función en algún punto dado junto con su tasa de cambio en ese punto.

Si f (x) es una función definida en un intervalo cerrado [a, a + h], entonces la cantidad de cambio de f (x) durante el intervalo es el cambio en los valores de la variable y de la función durante ese intervalo y está dada por

f (a + h) − f (a).

La tasa de cambio promedio de la función f durante ese mismo intervalo es la razón entre la cantidad de cambio de la función durante ese intervalo cerrado [a, a + h] y el cambio correspondiente en los valores de la variable independiente x. Esto es, la tasa de cambio promedio de una función f está dada por

Como ya sabemos, la tasa de cambio instantánea de f (x) en a es su derivada 

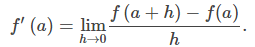
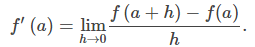
Para valores suficientemente pequeños de h, f ′(a)  ≈ [f (a + h) − f (a)]/h. Luego podemos despejar f (a + h) para obtener una estimación del nuevo valor de la función  para un incremento dado en la variable independiente:

Podemos usar esta fórmula si solo conocemos f (a) y f ′(a) y deseamos estimar el valor de f (a + h). Por ejemplo, podemos usar la población actual de una ciudad y la tasa a la que está creciendo para estimar su población en el futuro cercano. Como podemos ver en la Figura 3.4_1, estamos aproximando f (a + h) por la coordenada y en a + h en la recta tangente a f (x) en x = a. Observe que la precisión de esta estimación depende del valor de h, así como del valor de f ′ (a).

Ejemplo ilustrativo 3.4_1. Estimando el valor de una función

Si f (3) = 2 y f ′(3) = 5, estimar f (3.2).

Solución:

Comience por encontrar h. Tenemos que h = 3.2 − 3 = 0.2. Así,

♦

Ejercicio de control 3.4.1

Dado \(f(10) = -5\) y \(f'(10) = 6\), estima \(f(10.1)\). ♦

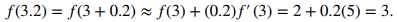
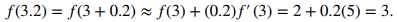
Movimiento a lo largo de una recta

Otro uso de la derivada es analizar el movimiento de una partícula a lo largo de una recta. Hemos descrito la velocidad como la tasa de cambio de la posición. Si tomamos la derivada de la velocidad, podemos encontrar la aceleración, o la tasa de cambio de la velocidad. También es importante introducir la idea de rapidez, que es la magnitud de la velocidad. Por lo tanto, podemos establecer las siguientes definiciones matemáticas.

DEFINICIÓN. Velocidad, rapidez y aceleración

Sea s(t) una función que proporciona la posición de un objeto en el tiempo t :

• La velocidad del objeto en el tiempo t viene dada por v(t) = s′(t).
• La rapidez del objeto en el tiempo t viene dada por |v(t)|.
• La aceleración del objeto en t viene dada por a(t) = v′(t) = s″(t). ♦

Ejemplo ilustrativo 3.4_2. Comparación de velocidad instantánea y velocidad media

Se deja caer una pelota desde una altura de 64 pies. Su altura sobre el suelo (en pies) t segundos después viene dada por s(t) = – 16t² + 64.

a. ¿Cuál es la velocidad instantánea de la pelota cuando toca el suelo?
b. ¿Cuál es la velocidad promedio durante su caída?

Solución:
Lo primero que debe hacer es determinar cuánto tiempo tarda la pelota en llegar al suelo. Para hacer esto, establezca s(t) = 0. Resolviendo −16t² + 64 = 0, obtenemos t = 2, por lo que la pelota tarda 2 segundos en llegar al suelo.

a. La velocidad instantánea de la pelota cuando golpea el suelo es v(2). Como v(t) = s′(t) = – 32t, obtenemos v(t) = – 64 pies/s.
b. La velocidad promedio de la pelota durante su caída es

♦

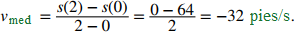
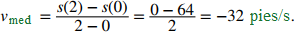
Ejemplo ilustrativo 3.4_3. Interpretación de la relación entre velocidad y aceleración

Una partícula se mueve a lo largo de un eje de coordenadas en la dirección positiva hacia la derecha. Su posición en el tiempo t viene dada por s(t) = t³ −4t + 2. Encuentre v(1) y a(1) y use estos valores para responder las siguientes preguntas.
a. ¿Se mueve la partícula de izquierda a derecha o de derecha a izquierda en el tiempo t = 1?
b. ¿Se está acelerando o desacelerando la partícula en el tiempo t = 1?

Solución:

Comience por encontrar v(t) y a(t).
v(t) = s′(t) = 3t² − 4 y a(t) = v(t) = s″(t) = 6t.
Al evaluar estas funciones en t = 1, obtenemos v(1) = – 1 y a(1) = 6.
a. Como v (1) < 0, la partícula se mueve de derecha a izquierda.
b. Como v(1) < 0 y a(1) > 0, la velocidad y la aceleración están actuando en direcciones opuestas. En otras palabras, la partícula se acelera en la dirección opuesta a la dirección en la que viaja, provocando que la rapidez|v (t)| disminuya. La partícula se está desacelerando. ♦

Ejemplo ilustrativo 3.4_4. Posición y velocidad

La posición de una partícula que se mueve a lo largo de un eje de coordenadas viene dada por s(t) = t³ − 9t² + 24t + 4, t ≥ 0.
a. Encuentra v(t).
b. ¿A qué hora (s) está la partícula en reposo?
c. ¿En qué intervalos de tiempo se mueve la partícula de izquierda a derecha? ¿De derecha a izquierda?
d. Utilice la información obtenida para dibujar la ruta de la partícula a lo largo de un eje de coordenadas.

Solución:
a. La velocidad es la derivada de la función de posición:

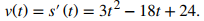
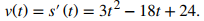
b. La partícula está en reposo cuando v(t) = 0, así que establezca 3t² − 18t + 24 = 0. Factorizar el lado izquierdo de la ecuación produce 3(t − 2)(t − 4) = 0. Resolviendo, encontramos que la partícula está en reposo en t = 2 y t = 4.

c. La partícula se mueve de izquierda a derecha cuando v(t) > 0 y de derecha a izquierda cuando v(t) < 0. La figura 3.4_2 proporciona el análisis del signo de v(t) para t ≥ 0, pero no representa el eje a lo largo del cual se mueve la partícula.

Como 3t² − 18t + 24 > 0 en [0, 2) ∪ (2, + ∞), la partícula se mueve de izquierda a derecha en estos intervalos.
Como 3t² − 18t + 24 < 0 en (2, 4), la partícula se mueve de derecha a izquierda en este intervalo.

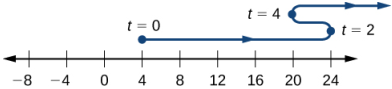
d. Antes de que podamos dibujar la gráfica del movimiento de la partícula, necesitamos saber su posición en el momento en que comienza a moverse (t = 0) y en los momentos en que cambia de dirección (t = 2,4). Tenemos s(0) = 4, s(2) = 24 y s(4) = 20. Esto significa que la partícula comienza en el eje de coordenadas en 4 y cambia de dirección en 0 y 20 en el eje de coordenadas. La trayectoria de la partícula se muestra en un eje de coordenadas en la figura 3.4_3.

♦

Ejercicio de control 3.4.2

Una partícula se mueve a lo largo de un eje de coordenadas. Su posición en el tiempo \(t\) está dada por \(s(t) = t^2 – 5t + 1\). ¿Se mueve la partícula de derecha a izquierda o de izquierda a derecha en el tiempo \(t = 3\)? ♦

Cambio poblacional

Además de analizar la velocidad, la rapidez, la aceleración y la posición, podemos usar derivados para analizar varios tipos de poblaciones, incluidas aquellas tan diversas como las colonias de bacterias y las ciudades. Podemos usar una población actual, junto con una tasa de crecimiento, para estimar el tamaño de una población en el futuro. La tasa de crecimiento de la población es la tasa de cambio de una población y, en consecuencia, puede representarse por la derivada del tamaño de la población.

DEFINICIÓN. Tasa de crecimiento de una población

Si P(t) es el número de individuos presentes en una población, entonces la tasa de crecimiento de la población P(t) se define como P′(t). ♦

Ejemplo ilustrativo 3.4_5. Estimando una Población

La población de una ciudad se triplica cada 5 años. Si su población actual es de 10,000, ¿cuál será su población aproximada dentro de 2 años?

Solución:

Sea P(t) la población (en miles) t años a partir de ahora. Por lo tanto, sabemos que P(0) = 10 y en base a la información, anticipamos P(5) = 30. Ahora se estima P′(0), la tasa de crecimiento actual, usando

Al aplicar la fórmula a P(t), podemos estimar la población dentro de 2 años escribiendo

así, en 2 años la población será de, aproximadamente, 18,000 individuos. ♦

Ejercicio de control 3.4.3

Se sabe que la población actual de una colonia de mosquitos es de 3000; es decir, \(P(0) = 3000\). Si \(P'(0) = 100\), estima el tamaño de la población en 3 días, donde \(t\) se mide en días. ♦

Cambios en costos e ingresos

Además de analizar el movimiento a lo largo de una recta y el crecimiento de la población, las derivadas son útiles para analizar los cambios en el costo, los ingresos y las ganancias. El concepto de una función marginal es común en los campos de los negocios y la economía e implica el uso de derivadas. El costo marginal es la derivada de la función de costo. El ingreso marginal es la derivada de la función de ingreso. La utilidad marginal es la derivada de la función de utilidad, que se basa en la función de costo y la función de ingresos.

DEFINICIÓN. Costo marginal, ingreso marginal y utilidad marginal

• Si C(x) es el costo de producir x artículos, entonces el costo marginal MC(x) es MC(x) = C′(x).
• Si R(x) es el ingreso obtenido de la venta de x artículos, entonces el ingreso marginal MR(x) es MR(x) = R′(x).
• Si P(x) = R(x) − C(x) es el beneficio obtenido de la venta de x artículos, entonces la utilidad marginal MP(x) se define como MP(x) = P(x) = MR(x ) − MC(x) = R′(x) − C(x). ♦

Podemos obtener una aproximación de

eligiendo un valor apropiado para h. Como x representa objetos, un valor razonable y pequeño para h es 1. Por lo tanto, al sustituir h = 1, obtenemos la aproximación MC(x) = C(x)  ≈ C′(x + 1) − C(x). En consecuencia, C′(x) para un valor dado de x puede considerarse como el cambio en el costo asociado con la producción de un artículo adicional. De manera similar, MR(x) = R′(x) se aproxima a los ingresos obtenidos por la venta de un artículo adicional, y MP(x) = P′(x) se aproxima a la ganancia obtenida al producir y vender un artículo adicional.

Ejemplo ilustrativo 3.4_6. Aplicando ingresos marginales

Suponga que el número de cenas de barbacoa, x, que se pueden vender está relacionado con el precio cobrado, p, por la ecuación p(x) = 9 − 0.03x, 0 ≤ x ≤ 300.

En este caso, los ingresos en dólares obtenidos al vender x cenas de barbacoa están dados por

Use la función de ingresos marginales para estimar los ingresos obtenidos de la venta de la 101-ava cena de barbacoa. Compare esto con los ingresos reales obtenidos de la venta de esta cena.

Solución:

Primero, encuentre la función de ingreso marginal: MR(x) = R′(x) = – 0.06x + 9.
Luego, use R′(100) para aproximar R(101) − R(100), los ingresos obtenidos de la venta de la 10.ava cena. Dado que R′(100) = 3, los ingresos obtenidos de la venta de la cena número 101 son de aproximadamente $3.

Los ingresos reales obtenidos de la venta de la 101ª cena son

El ingreso marginal es una estimación bastante buena en este caso y tiene la ventaja de ser fácil de calcular. ♦

Ejercicio de control 3.4.4

Suponga que la ganancia obtenida por la venta de \(x\) cenas de pescado frito está dada por \(P(x) = -0.03x^2 + 8x – 50\). Use la función de ganancia marginal para estimar la ganancia de la venta de la cena de pescado frito número 101. ♦