La regla de la cadena: Objetivos de aprendizaje
3.6.1. Indique la regla de la cadena para la composición de dos funciones.
3.6.2. Aplica la regla de la cadena junto con la regla de la potencia.
3.6.3. Aplique la regla de la cadena y las reglas del producto / cociente correctamente en combinación cuando ambas sean necesarias.
3.6.4. Reconocer la regla de la cadena para una composición de tres o más funciones.
3.6.5. Describa la prueba de la regla de la cadena.
Hemos visto las técnicas para diferenciar funciones básicas (xⁿ, senx, cosx, etc.) así como sumas, diferencias, productos, cocientes y múltiplos constantes de estas funciones. Sin embargo, estas técnicas no nos permiten diferenciar composiciones de funciones, como h(x) = sen(x³) o k(x) = √(3x² + 1). En esta sección, estudiamos la regla para encontrar la derivada de la composición de dos o más funciones.
Deduciendo la regla de la cadena
Cuando tenemos una función que es una composición de dos o más funciones, podríamos usar todas las técnicas que ya hemos aprendido para diferenciarla. Sin embargo, usar todas esas técnicas para dividir una función en partes más simples que podamos diferenciar puede volverse engorroso. En su lugar, usamos la regla de la cadena, que establece que la derivada de una función compuesta es la derivada de la función externa evaluada en la función interna multiplicada por la derivada de la función interna.
Para poner esta regla en contexto, veamos un ejemplo: h(x) = sen(x³). Podemos pensar en la derivada de esta función con respecto a x como la tasa de cambio de sen(x³) en relación con el cambio en x. En consecuencia, queremos saber cómo cambia sen(x³) a medida que x cambia. Podemos pensar en este evento como una reacción en cadena: a medida que x cambia, x³ cambia, lo que conduce a un cambio en sen(x³). Esta reacción en cadena nos da pistas sobre lo que implica calcular la derivada de sen(x³). En primer lugar, un cambio en x que fuerza un cambio en x³ sugiere que de alguna manera está involucrada la derivada de x³. Además, el cambio en x³ forzando un cambio en sen(x³) sugiere que la derivada de sen(u) con respecto a u, donde u = x³, también es parte de la derivada final.
Podemos echar un vistazo más formal a la derivada de h(x) = sen(x³) estableciendo el límite que nos daría la derivada en un valor específico de a en el dominio de h(x) = sen(x³) .
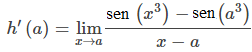
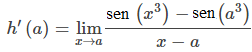
Esta expresión no parece particularmente útil; sin embargo, podemos modificarlo multiplicando y dividiendo por la expresión x³ − a³ para obtener
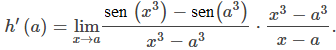
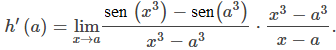
De la definición de la derivada, podemos ver que el segundo factor es la derivada de x³ en x = a. Es decir,
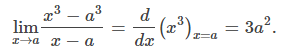
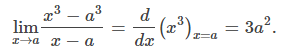
Sin embargo, podría ser un poco más difícil reconocer que el primer término también es una derivada. Podemos ver esto dejando u = x³ y observando que cuando x → a, u → u³:
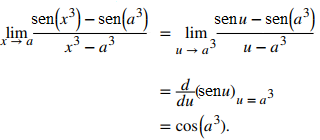
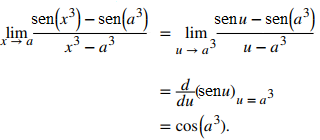
Esto es,
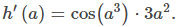
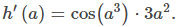
En otras palabras, si h(x) = sen(x³), entonces h′(x) = cos(x³) ⋅3x². Por lo tanto, si pensamos en h(x) = sen(x³) como la composición (f ∘ g) (x) = f (g(x)) donde f (x) = senx y g(x) = x³, entonces la derivada de h(x) = sen(x³) es el producto de la derivada de g(x) = x³ y la derivada de la función f (x) = senx evaluada en la función g(x) = x³. En este punto, anticipamos que para h(x) = sen(g(x)), es bastante probable que h′(x) = cos (g(x)) g(x). Como determinamos anteriormente, este es el caso de h(x) = sen(x³).
Ahora que hemos estudiado un caso especial de la regla de la cadena, establecemos el caso general y luego aplicamos esta forma general a otras funciones compuestas. Se proporciona una prueba informal al final de la sección.
REGLA 3.6_1: LA REGLA DE CADENA
|
Sean f y g dos funciones. Para todas las x en el dominio de g para las cuales g es diferenciable en x y f es diferenciable en g(x), la derivada de la función compuesta
está dada por
Alternativamente, si y es una función de u, y asu vez u es una función de x, entonces
|
ESTRATEGIA DE RESOLUCIÓN DE PROBLEMAS: APLICACIÓN DE LA REGLA DE CADENA
Nota: Al aplicar la regla de la cadena a la composición de dos o más funciones, tenga en cuenta que trabajamos desde la función externa hacia adentro. También es útil recordar que la derivada de la composición de dos funciones puede considerarse como que tiene dos partes; la derivada de la composición de tres funciones tiene tres partes; y así. Además, recuerde que nunca evaluamos una derivada en una derivada. |
Las reglas de la cadena y de la potencia combinadas
Ahora podemos aplicar la regla de la cadena a funciones compuestas, pero tenga en cuenta que a menudo necesitamos usarla con otras reglas. Por ejemplo, para encontrar derivadas de funciones de la forma h(x) = (g(x))ⁿ, necesitamos usar la regla de la cadena combinada con la regla de la potencia. Para hacerlo, podemos pensar en h(x)= (g(x))ⁿ como f(g(x)) donde f (x) = xⁿ. Entonces f ′(x) = nxⁿ⁻ ¹. Por lo tanto, f ′(g(x))) = n(g(x))ⁿ⁻ ¹. Esto nos lleva a la derivada de una función potencia usando la regla de la cadena,
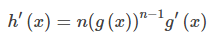
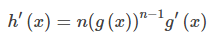
REGLA 3.6_2: REGLA DE la potencia PARA LA COMPOSICIÓN DE FUNCIONES
|
Para todos los valores de x para los que se define la derivada, si
Entonces
|
Ejemplo ilustrativo 3.6_1. Usando las reglas la cadena y de la potencia
Encuentre la derivada de h(x) = 1/(3x² + 1)².
Solución:
Primero, reescribe h(x) = 1/(3x² + 1)² = (3x² + 1)⁻².
Aplicando la regla de la potencia con g(x) = 3x² + 1, tenemos


Reescribir de nuevo a la forma original nos da
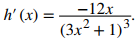
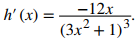
◊
Ejemplo ilustrativo 3.6_2. Uso de las reglas de la cadena y y de la potencia con una función trigonométrica
Encuentre la derivada de h(x) = sen³x.
Solución:
Primero recuerde que sen³x = (senx)³, por lo que podemos reescribir h(x) = sen³x como h(x) = (senx)³.
Aplicando la regla de la potencia con g(x) = senx, obtenemos
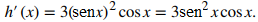
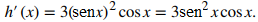
Ejemplo ilustrativo 3.6_3. Encontrar la ecuación de una recta tangente
Encuentre la ecuación de una recta tangente a la gráfica de h(x) = 1/(3x − 5)² en x = 2.
Solución:
Debido a que estamos encontrando la ecuación de una recta, necesitamos un punto. La coordenada x del punto es 2. Para encontrar la coordenada y, sustituye 2 en h(x). Como h(2) = 1/(3(2) − 5)² = 1, el punto es (2, 1).
Para la pendiente, necesitamos h′(2). Para encontrar h′(x), primero reescribimos h(x) = (3x − 5)⁻² y aplicamos la regla de la potencia para obtener
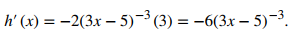
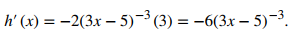
Al sustituir, tenemos h′(2) = – 6(3(2) −5)⁻³ = −6. Por lo tanto, la recta tiene la ecuación y − 1 = −6(x − 2). Reescribiendo, la ecuación de la recta es y = −6x + 13. ◊





