| 9. Ecuaciones diferenciales | 9.5 Ecuaciones lineales de segundo orden |
9.5.3 Ecuaciones lineales no homogéneas
Ahora consideraremos la ecuación lineal no homogénea de segundo orden
y″ + p(x)y′ + q(x)y = f (x), (9.5.3.1)
donde la función de forzamiento f no es idénticamente cero. El siguiente teorema, una extensión del Teorema 9.5.1.1, da condiciones suficientes para la existencia y unicidad de soluciones de problemas de valor inicial para (9.5.3.1). Omitimos la prueba, que está más allá del alcance de este libro.
Teorema 9.5.3.1
Suponga que p, q y f son continuas en un intervalo abierto (a, b), sea x0 cualquier punto en (a, b), y sean k0 y k1 números reales arbitrarios. Entonces el problema de valor inicial
y″ + p(x)y′ + q(x)y = f (x), y(x0) = k0, y′(x0) = k1
tiene solución única en (a, b). ♦
Para encontrar la solución general de (9.5.3.1) en un intervalo (a, b) donde p, q y f son continuas, es necesario encontrar la solución general de la ecuación homogénea asociada
y″ + p(x)y′ + q(x)y = 0, (9.5.3.2)
en (a, b). Llamamos a (9.5.3.2) la ecuación complementaria de (9.5.3.1).
El siguiente teorema muestra cómo encontrar la solución general de (9.5.3.1) si conocemos una solución yp de (9.5.3.1) y un conjunto fundamental de soluciones de (9.5.3.2). Llamamos yp a una solución particular de (9.5.3.1); puede ser cualquier solución que podamos encontrar, de una forma u otra.
Teorema 9.5.3.2
Suponga que p, q y f son continuas en (a, b). Sea yp una solución particular de
y″ + p(x)y′ + q(x)y = f (x), (9.5.3.3)
en (a, b), y sea {y1, y2} un conjunto fundamental de soluciones de la ecuación complementaria
y″ + p(x)y′ + q(x)y = 0, (9.5.3.4)
en (a, b). Entonces y es una solución de (9.5.3.3) en (a, b) si y solo si
y = yp + c1y1 + c2y2, (9.5.3.5)
donde c1 y c2 son constantes. ♦
Prueba:
Primero mostramos que y en (9.5.3.5) es una solución de (9.5.3.3) para cualquier elección de las constantes c1 y c2.
Derivando (9.5.3.5) dos veces se obtiene
y′ = yp′ + c1y1′ + c2y2′ y y′′ = yp′′ + c1y1′′ + c2y2′′,
así que


ya que yp satisface (9.5.3.3) y y1 e y2 satisfacen (9.5.3.4).
Ahora mostraremos que cada solución de (9.5.3.3) tiene la forma (9.5.3.5) para alguna elección de las constantes c1 y c2. Suponga que y es una solución de (9.5.3.3). Mostraremos que y − yp es una solución de (9.5.3.4), y por lo tanto de la forma y − yp = c1y1 + c2y2, lo que implica (9.5.3.5). Para ver esto, calculamos


ya que y e yp satisfacen (9.5.3.3). ♦
Decimos que (9.5.3.5) es la solución general de (9.5.3.3) sobre (a, b).
Si P0, P1 y F son continuas y P0 no tiene ceros en (a, b), entonces el teorema 9.5.3.2 implica que la solución general de
P0(x)y′′ + P1(x)y′ + P2(x)y = F(x) (9.5.3.6)
en (a, b) es y = yp + c1y1 + c2y2, donde yp es una solución particular de (9.5.3.6) en (a, b) y {y1, y2} es un conjunto fundamental de soluciones de
P0(x)y′′ + P1(x)y′ + P2(x)y = 0
en (a, b). Para ver esto, reescribimos (9.5.3.6) como
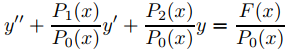
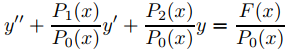
y aplique el Teorema 9.5.3.2 con p = P1/P0, q = P2/P0 y f = F/P0.
Para evitar una redacción incómoda en ejemplos y ejercicios, no especificaremos el intervalo (a, b) cuando preguntemos por la solución general de una ecuación lineal de segundo orden específica, o por un conjunto fundamental de soluciones de una ecuación lineal homogénea de segundo orden. Acordemos que esto siempre significa que queremos la solución general (o un conjunto fundamental de soluciones, según sea el caso) en cada intervalo abierto en el que p, q y f son continuas si la ecuación es de la forma (9.5. 3.3), o en el que P0, P1, P2 y F son continuos y P0 no tiene ceros, si la ecuación es de la forma (9.5.3.6). Le dejamos a usted identificar estos intervalos en ejemplos y ejercicios específicos.
Para completar, señalamos que si P0, P1, P2 y F son todos continuos en un intervalo abierto (a, b), pero P0 tiene un cero en (a, b), entonces (9.5.3.6) puede fallar en tener una solución general en (a, b) en el sentido recién definido. Los ejercicios 42 a 44 ilustran este punto para una ecuación homogénea.
En esta sección nos limitaremos a las aplicaciones del Teorema 9.5.3.2 donde podemos adivinar la forma de la solución particular.
Ejemplo ilustrativo 9.5.3.1
(a) Encuentre la solución general de
y″ + y = 1. (9.5.3.7)
(b) Resuelva el problema de valor inicial
y″ + y = 1, y(0) = 2, y′(0) = 7. (9.5.3.8)
Solución:
(a) Podemos aplicar el Teorema 9.5.3.2 con (a, b) = (−∞, ∞), ya que las funciones p ≡ 0, q ≡ 1 y f ≡ 1 en (9.5.3.7) son continuas en (−∞, ∞ ). Por inspección vemos que yp ≡ 1 es una solución particular de (9.5.3.7). Como y1 = cosx e y2 = senx forman un conjunto fundamental de soluciones de la ecuación complementaria y″ + y = 0, la solución general de (9.5.3.7) es
y = 1 + c1cosx + c2senx. (9.5.3.9)
(b) Al imponer la condición inicial y(0) = 2 en (9.5.3.9) se obtiene 2 = 1 + c1, por lo que c1 = 1. Derivando (9.5.3.9) se obtiene
y′ = − c1senx + c2cosx.
Al imponer la condición inicial y′(0) = 7 aquí se obtiene c2 = 7, por lo que la solución de (9.5.3.8) es
y = 1 + cosx + 7senx.
La Figura 9.5.3.1 es un gráfico de esta función.

Ejemplo ilustrativo 9.5.3.2
(a) Encuentre la solución general de
y″ − 2y′ + y = −3 − x + x2. (9.5.3.10)
(b) Resuelva el problema de valor inicial
y″ − 2y′ + y = −3 − x + x2, y(0) = −2, y′(0) = 1. (9.5.3.11)
Solución:
(a) El polinomio característico de la ecuación complementaria
y″ − 2y′ + y = 0
es r2 − 2r + 1 = (r − 1)2, por lo que y1 = ex y y2 = xex forman un conjunto fundamental de soluciones de la ecuación complementaria. Para adivinar una forma para una solución particular de (9.5.3.10), observamos que al sustituir un polinomio de segundo grado yp = A + Bx + Cx2 en el lado izquierdo de (9.5.3.10) se producirá otro polinomio de segundo grado con coeficientes que dependen sobre A, B y C. El truco consiste en elegir A, B y C. de modo que los polinomios de los dos lados de (9.5.3.10) tengan los mismos coeficientes; por lo tanto, si
yp = A + Bx + Cx2 entonces yp′ = B + 2Cx y yp″ = 2C,
así que


Igualando coeficientes de potencias iguales de x en los dos lados de la última igualdad se obtiene


entonces C = 1, B = −1 + 4C = 3 y A = −3 − 2C + 2B = 1. Por lo tanto, yp = 1 + 3x + x2 es una solución particular de (9.5.3.10) y el Teorema 9.5.3.2 implica que
y = 1 + 3x + x2 + ex(c1 + c2x) (9.5.3.12)
es la solución general de (9.5.3.10).
(b) Al imponer la condición inicial y(0) = −2 en (9.5.3.12) se obtiene −2 = 1 + c1, por lo que c1 = −3. Diferenciando (9.5.3.12) obtenemos
y′ = 3 + 2x + ex(c1 + c2x) + c2ex,
e imponiendo la condición inicial y′0) = 1 aquí se obtiene 1 = 3 + c1+ c2, por lo que c2 = 1. Por lo tanto, la solución de (9.5.3.11) es
y = 1 + 3x + x2 − ex(3 − x).
La Figura 9.5.3.2 es un gráfico de esta solución.


Ejemplo ilustrativo 9.5.3.3
(Encuentre la solución general de
x2y″ + xy′ − 4y = 2x4 (9.5.3.13)
en (−∞, 0) y (0, ∞)
Solución:
En el Ejemplo 9.5.1.3, verificamos que y1 = x2 e y2 = 1/x2 forman un conjunto fundamental de soluciones de la ecuación complementaria
x2y″ + xy′ − 4y = 0
en (−∞, 0) y (0, ∞). Para encontrar una solución particular de (9.5.3.13), observamos que si yp = Ax4, donde A es una constante, ambos lados de (9.5.3.13) serán múltiplos constantes de x4 y podemos elegir A de modo que los dos lados sean iguales. Esto es cierto en este ejemplo, ya que si yp = Ax4 entonces


si A = 1/6; por lo tanto, yp = x4/6 es una solución particular de (9.5.3.13) sobre (−∞, ∞). El teorema 9.5.3.2 implica que la solución general de (9.5.3.13) en (−∞, 0) y (0, ∞) es
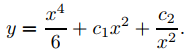
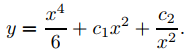
El principio de superposición
El siguiente teorema nos permite dividir una ecuación no homogénea en partes más simples, encontrar una solución particular para cada parte y luego combinar sus soluciones para obtener una solución particular del problema original.
Teorema 9.5.3.3 [El principio de superposición]
Suponga que yp1 es una solución particular de
y″ + p(x)y′ + q(x)y = f1(x)
en (a, b) y yp2 es una solución particular de
y″ + p(x)y′ + q(x)y = f2(x)
en (a, b). Entonces
yp = yp1 + yp2
es una solución particular de
y″ + p(x)y′ + q(x)y = f1(x) + f2(x)
en (a, b). ♦
Prueba
Si yp = yp1 + yp2 entonces


Es fácil generalizar el Teorema 9.5.3.3 a la ecuación
y′′ + p(x)y′ + q(x)y = f (x) (9.5.3.14)
donde
f = f1 + f2 + · · · + fk;
por lo tanto, si ypi es una solución particular de
y′′ + p(x)y′ + q(x)y = fi(x)
en (a, b) para i = 1, 2, . . . , k, entonces yp1 + yp2 + · · · + ypk es una solución particular de (9.5.3.14) en (a, b). Además, mediante una demostración similar a la demostración del Teorema 9.5.3.3 podemos formular el principio de superposición en términos de una ecuación lineal escrita en la forma
P0(x)y′′ + P1(x)y′ + P2(x)y = F(x)
(Ejercicio 39); es decir, si yp1 es una solución particular de
P0(x)y′′ + P1(x)y′ + P2(x)y = F1(x)
en (a, b) y yp2 es una solución particular de
P0(x)y′′ + P1(x)y′ + P2(x)y = F2(x)
en (a, b), entonces yp1 + yp2 es una solución de
P0(x)y′′ + P1(x)y′ + P2(x)y = F1(x) + F2(x)
en (a, b).
Ejemplo ilustrativo 9.5.3.4
La función yp1 = x4/15 es una solución particular de
x2y′′ + 4xy′ + 2y = 2x4 (9.5.3.15)
en (−∞, ∞) y yp2 = x2/3 es una solución particular de
x2y′′ + 4xy′ + 2y = 4x2 (9.5.3.16)
en (−∞, ∞). Usar el principio de superposición para encontrar una solución particular de
x2y′′ + 4xy′ + 2y = 2x4 + 4x2 (9.5.3.17)
en (−∞, ∞).
Solución:
El lado derecho F(x) = 2x4 + 4x2 en (9.5.3.17) es la suma de los lados derechos
F1(x) = 2x4 y F2(x) = 4x2.
en (9.5.3.15) y (9.5.3.16). Por tanto, el principio de superposición implica que


es una solución particular de (9.5.3.17). ♦
