| 5. La integral y Técnicas de integración | Ejercicios propuestos para el Capítulo 5.6 |
5.6 Integrales que implican funciones exponenciales y logarítmicas
Objetivos de aprendizaje:
5.6.1. Integrar funciones que involucran funciones exponenciales.
5.6.2. Integrar funciones que involucran funciones logarítmicas.
Las funciones exponenciales y logarítmicas se utilizan para modelar el crecimiento de una población, el crecimiento celular y el crecimiento financiero, así como la depreciación, la desintegración radiactiva y el consumo de recursos, por nombrar solo algunas aplicaciones. En esta sección, exploramos la integración que involucra funciones exponenciales y logarítmicas.
Integrales de funciones exponenciales
La función exponencial es quizás la función más eficiente en términos de las operaciones de cálculo. La función exponencial, y = eˣ es su propia derivada y su propia integral.
REGLA 5.6.1: INTEGRALES DE FUNCIONES EXPONENCIALES
Las funciones exponenciales pueden integrarse usando las siguientes fórmulas.
\(\int e^x dx = e^x + C\)
\(\int a^x dx = \frac{a^x}{\ln a} + C\)
♦
EJEMPLO ILUSTRATIVO 5.6_1. Encontrar la antiderivada de una función exponencial
Encuentre la antiderivada de la función exponencial e⁻x.
Solución:
Utilice la sustitución u, estableciendo u = −x, y luego du = −dx. Multiplique la ecuación du por −1, de modo que ahora tenga −du = dx. Entonces,
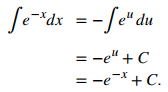 ♦
♦
Ejercicio de control 5.6.1
Encuentra la antiderivada de la función usando sustitución u: \(x^2 e^{-2x^3}\). ♦
Un error común al tratar con expresiones exponenciales es tratar el exponente de e de la misma manera que tratamos los exponentes en las expresiones polinómicas. No podemos usar la regla de la potencia para el exponente de e. Esto puede ser especialmente confuso cuando tenemos exponenciales y polinomios en la misma expresión, como en el punto de control anterior. En estos casos, siempre debemos verificar dos veces para asegurarnos de que estamos utilizando las reglas correctas para las funciones que estamos integrando.
EJEMPLO ILUSTRATIVO 5.6_2. Raíz cuadrada de una función exponencial
Encuentre la antiderivada de la función exponencial ex √(1 + ex).
Solución:
Primero reescribe la raíz usando un exponente racional:

Usando la sustitución u = 1 + eˣ, entonces, du = eˣdx. Tenemos (Figura 5.6_1)

Entonces,


Figura 5.6_1 El gráfico muestra una función exponencial multiplicada por la raíz cuadrada de una función exponencial. ♦
Ejercicio de control 5.6.2
Encuentra la antiderivada de \(e^x(3e^x – 2)^2\). ♦
EJEMPLO ILUSTRATIVO 5.6_3. Usar sustitución u con una función exponencial
Usar sustitución u para evaluar la integral indefinida

Solución:
Aquí elegimos u para que sea el exponente en e. Sea u = 2x³ entonces du = 6x²dx. La función original contiene un factor de 3x², no 6x². Multiplica ambos lados de la ecuación por 1/2 para que el integrando en u sea igual al integrando en x. Así,

Integre la expresión en u y luego sustituya la expresión original en x nuevamente en la integral u:

♦
Ejercicio de control 5.6.3
Evalúa la integral indefinida \(\int 2x^3 e^{x^4} dx\). ♦
Como se mencionó al principio de esta sección, las funciones exponenciales se utilizan en muchas aplicaciones de la vida real. El número e a menudo se asocia con un crecimiento compuesto o acelerado, como hemos visto en secciones anteriores sobre la derivada. Aunque la derivada representa una tasa de cambio o una tasa de crecimiento, la integral representa el cambio total o el crecimiento total. Veamos un ejemplo en el que la integración de una función exponencial resuelve una aplicación comercial común.
Una función precio-demanda nos dice la relación entre la cantidad demandada de un producto y el precio del producto. En general, el precio disminuye a medida que aumenta la cantidad demandada. La función precio-demanda marginal es la derivada de la función precio-demanda y nos dice qué tan rápido cambia el precio en un nivel de producción dado. Estas funciones se utilizan en los negocios para determinar la elasticidad precio – demanda y así ayudar a las empresas a determinar si cambiar los niveles de producción sería rentable.
EJEMPLO ILUSTRATIVO 5.6_4. Encontrar una ecuación precio-demanda
Encuentre la ecuación precio-demanda para una marca particular de pasta de dientes en una cadena de supermercados cuando la demanda es de 50 tubos por semana a $ 2.35 por tubo, dado que el precio marginal-función de demanda, p′(x), para x número de tubos por semana, se da como

Si la cadena de supermercados desea vender 100 tubos por semana, ¿qué precio debería establecer?
Solución:
Para encontrar la ecuación precio-demanda, integre la función marginal precio-demanda. Primero encuentre la antiderivada, luego mire los detalles. Así,
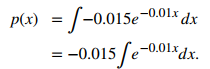
Usando la sustitución u, sea u = −0.01x entonces du = −0.01dx. Luego, divide ambos lados de la ecuación du por −0.01. Esto da
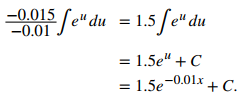
El siguiente paso es hallar el valor de C. Sabemos que cuando el precio es de $ 2.35 por tubo, la demanda es de 50 tubos por semana. Esto significa

Ahora, solo despeja C:

Así,

Si el supermercado vende 100 tubos de pasta de dientes por semana, el precio sería

El supermercado debería cobrar $ 1.99 por tubo si está vendiendo 100 tubos por semana. ♦
EJEMPLO ILUSTRATIVO 5.6_5. Evaluación de una integral definida que involucra una función exponencial
Evaluar la integral definida

Solución:
Nuevamente, el método más conveniente a utilizar es la sustitución u. Sea u = 1 − x, entonces du = −dx o −du = dx. Entonces

A continuación, cambie los límites de la integración. Usando la ecuación u = 1 − x, tenemos

La integral se convierte en


Figura 5.6_2 El área indicada se puede calcular evaluando una integral definida utilizando la sustitución u. ♦
Ejercicio de control 5.6.4
Evalúa \(\int_{0}^{2} e^{2x} dx\). ♦
EJEMPLO ILUSTRATIVO 5.6_7. Crecimiento de bacterias en un cultivo
Suponga que la tasa de crecimiento de bacterias en una placa de Petri viene dada por q(t) = 3 ͭ , donde t se da en horas y q(t) se da en miles de bacterias por hora. Si un cultivo comienza con 10,000 bacterias, encuentre una función Q(t) que proporcione el número de bacterias en la placa de Petri en cualquier momento t. ¿Cuántas bacterias hay en el plato después de 2 horas?
Solución:
Tenemos

Entonces, en t = 0 tenemos Q(0) = 10 = 1/ln3 + C, entonces C ≈ 9.090 y obtenemos

En el tiempo t = 2, tenemos

Después de 2 horas, hay 17.282 bacterias en el plato. ♦
Ejercicio de control 5.6.5
Del Ejemplo 5.6.7, suponga que las bacterias crecen a una tasa de \(q(t) = 2^t\). Asuma que el cultivo aún comienza con 10,000 bacterias. Encuentre \(Q(t)\). ¿Cuántas bacterias hay en la placa después de 3 horas? ♦
EJEMPLO ILUSTRATIVO 5.6_8. Mosca de la fruta. Crecimiento de una población
Supongamos que una población de moscas de la fruta aumenta a un ritmo de

en moscas por día. Si la población inicial de moscas de la fruta es de 100 moscas, ¿cuántas moscas hay en la población después de 10 días?
Solución:
Supongamos que G(t) representa el número de moscas en la población en el momento t. Aplicando el teorema del cambio neto, tenemos

Hay 122 moscas en la población después de 10 días. ♦
Ejercicio de control 5.6.6
Suponga que la tasa de crecimiento de la población de moscas está dada por \(g(t) = e^{0.01t}\), y la población inicial de moscas es de 100 moscas. ¿Cuántas moscas hay en la población después de 15 días? ♦
EJEMPLO ILUSTRATIVO 5.6_9. Evaluación de una integral definida usando sustitución u
Evalúe la integral definida usando sustitución u:
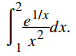
Solución:
Este problema requiere una reescritura para simplificar la aplicación de las propiedades. Primero, reescribe el exponente en e como una potencia de x, luego lleva la x² en el denominador hasta el numerador usando un exponente negativo. Tenemos

Sea u = x−1, el exponente en e. Entonces
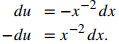
Trayendo el signo negativo fuera del signo integral, el problema ahora se lee

A continuación, cambie los límites de integración:

Observe que ahora los límites comienzan con el número mayor, lo que significa que debemos multiplicar por −1 e intercambiar los límites. Así,

♦
Ejercicio de control 5.6.7
Evalúa la integral definida usando la sustitución: \(\int_{1}^{2} \frac{1}{x^3} e^{4x^{-2}}dx\). ♦
Integrales que implican funciones logarítmicas
La integración de funciones de la forma \(f(x) = x^{-1}\) da como resultado el valor absoluto de la función logaritmo natural, como se muestra en la siguiente regla. Las fórmulas integrales para otras funciones logarítmicas, tales como \(f(x) = \ln x\) y \(f(x) = \log_a x\), también se incluyen en la regla.
REGLA 5.6.2: FÓRMULAS DE INTEGRACIÓN QUE INCLUYEN FUNCIONES LOGARÍTMICAS
Las siguientes fórmulas se pueden usar para evaluar integrales que involucran funciones logarítmicas.
\(\begin{aligned} \int x^{-1} dx &= \ln |x| + C \\ \int \ln x dx &= x \ln x – x + C = x (\ln x – 1) + C \\ \int \log_a x dx &= \frac{x}{\ln a}(\ln x – 1) + C \end{aligned}\)
♦
EJEMPLO ILUSTRATIVO 5.6_10. Encontrar una antiderivada que involucra lnx
Encuentre la antiderivada de la función 3/(x − 10).
Solución:
Primero factoriza el 3 fuera del símbolo integral. Luego usa la regla u−1. Así,


Figura 5.6_3 El dominio de esta función implica x ≠ 10.
Ejercicio de control 5.6.8
Encuentra la antiderivada de \(\frac{1}{x+2}\). ♦
EJEMPLO ILUSTRATIVO 5.6_11. Encontrar una antiderivada de una función racional
Encuentra la antiderivada de La función a integrar puede reescribirse como
La función a integrar puede reescribirse como
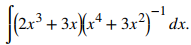
Usar sustitución u. Sea u = x⁴ + 3x², luego du = 4x³ + 6x. Cambiamos du factorizando por 2. Por lo tanto,

Reescribe el integrando en términos de u:

Entonces obtenemos

♦
EJEMPLO ILUSTRATIVO 5.6_12. Encontrar la antiderivada de una función logarítmica
Encuentre la antiderivada de la función logarítmica log2x.
Solución:
Siga el formato en la fórmula que figura en la regla sobre fórmulas de integración que involucran funciones logarítmicas. En base a este formato, tenemos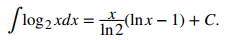 ♦
♦
Ejercicio de control 5.6.9
Encuentra la antiderivada de \(\log_3 x\). ♦
En el ejemplo 5.6_13 se tiene una integral definida de una función trigonométrica. Con las funciones trigonométricas, a menudo tenemos que aplicar una propiedad trigonométrica o una identidad antes de poder avanzar. Encontrar la forma correcta del integrando suele ser la clave para una integración fluida.
EJEMPLO ILUSTRATIVO 5.6_13. Evaluación de una integral definida
Encuentra la integral definida de

Solución:
Necesitamos sustitución u para resolver este problema. Sea u = 1 + cosx, entonces du = −senxdx. Reescribe la integral en términos de u, cambiando también los límites de integración. Así,

Entonces,

♦

Los ejercicios de aplicación son muy interesantes.
Más adelante podrá ver ejercicios de aplicación similares en el capítulo sobre ecuaciones diferenciales https://calculo21.com/ecuaciones-diferenciales/ 👀