7. Sucesiones y series infinitas
- 7.7 Series de potencias y funciones
- 7.8 Propiedades de las series de potencias
- 7.9 Series de Taylor y Maclaurin
- 7.10 Trabajando con series de Taylor
El copo de nieve de Koch se construye a partir de un número infinito de triángulos equiláteros no superpuestos. En consecuencia, podemos expresar su área como una suma de infinitos términos. ¿Cómo agregamos un número infinito de términos? ¿Puede una suma de un número infinito de términos ser finita? Para responder a estas preguntas, necesitamos introducir el concepto de una serie infinita, una suma con infinitos términos. Una vez definidas las herramientas necesarias, podremos calcular el área del copo de nieve de Koch, por ejemplo.
El tema de las series infinitas puede parecer ajeno al cálculo diferencial e integral. De hecho, una serie infinita cuyos términos involucran potencias de una variable es una herramienta poderosa que podemos usar para expresar funciones como “polinomios infinitos”. Podemos usar series infinitas para evaluar funciones complicadas, aproximar integrales definidas y crear nuevas funciones. Además, se utilizan series infinitas para resolver ecuaciones diferenciales que modelan el comportamiento físico, desde pequeños circuitos electrónicos hasta satélites en órbita terrestre.
El área del copo de Koch es finita y su contorno (frontera) es infinita.
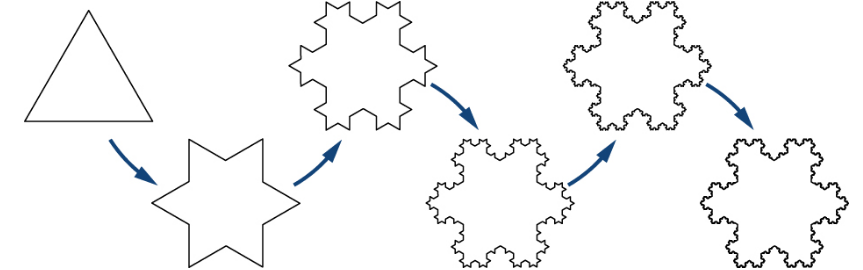
El copo de nieve de Koch se puede construir partiendo de un triángulo equilátero, a continuación, alterando de forma recursiva cada segmento de línea como sigue:
dividir el segmento de línea en tres segmentos de igual longitud.
dibujar una equilátero triángulo que tiene el segmento medio de la etapa 1 como su base y los puntos hacia el exterior.
eliminar el segmento de línea que es la base del triángulo de la etapa 2.
Después de una iteración de este proceso, la forma resultante es el esquema de un hexagrama .
El copo de nieve de Koch es el límite acercado como los pasos anteriores se siguen una y otra vez. La curva de Koch descrita originalmente por Helge von Koch está construido con sólo uno de los tres lados del triángulo original. En otras palabras, tres curvas de Koch hacen un copo de nieve de Koch.
El ejercicio numero 3 resulta sucesión infinita
En el ejemplo tres se tiene una sucesión finita👀
Si la sucesión sigue para siempre, es una sucesión infinita,
si no es una sucesión finita
Ejemplos:
{1, 2, 3, 4 ,…} es una sucesión muy simple (y es una sucesión infinita)
{20, 25, 30, 35, …} también es una sucesión infinita
{1, 3, 5, 7} es la sucesión de los 4 primeros números impares (y es una sucesión infinita)
{4, 3, 2, 1} va de 4 a 1 hacia atrás
{1, 2, 4, 8, 16, 32, …} es una sucesión infinita donde vamos duplicando cada término
{a, b, c, d, e} es la sucesión de las 5 primeras letras en order alfabético
{a, l, f, r, e, d, o} es la sucesión de las letras en el nombre “alfredo”
{0, 1, 0, 1, 0, 1, …} es la sucesión que alterna 0s y 1s (sí, siguen un orden, en este caso un orden alternativo)
Las secuencias también usan la misma notación que los conjuntos:
se enumera cada elemento, separados por una coma,
y luego se ponen llaves alrededor de todo. {3, 5, 7, …}
Los corchetes { } también se conocen como “llaves”.
Una sucesión sigue una regla que te dice cómo calcular el valor de cada término.
Ejemplo: la sucesión {3, 5, 7, 9, …} empieza por 3 y salta 2 cada vez:
{3, 5, 7, 9, …}