| 9. Ecuaciones diferenciales | 9.8. La transformada de Laplace | Ejercicios propuestos para el Capítulo 9.8.5 |
9.8.5 Ecuaciones de coeficientes constantes con funciones de forzamiento continuas por tramos
Ahora consideraremos problemas de valor inicial de la forma
 (9.8.5.1)
(9.8.5.1)
donde a, b y c son constantes (a ≠ 0) y f es continua por tramos en [0, ∞). Los problemas de este tipo ocurren en situaciones en las que la entrada a un sistema físico sufre cambios instantáneos, como cuando se enciende o apaga un interruptor o cuando las fuerzas que actúan sobre el sistema cambian abruptamente.
Puede demostrarse (Ejercicios 23 y 24) que la ecuación diferencial en (9.8.5.1) no tiene soluciones en un intervalo abierto que contiene una discontinuidad de salto de f. Por lo tanto, debemos definir qué entendemos por solución de (9.8.5.1) en [0, ∞) en el caso de que f tenga saltos discontinuos. El siguiente teorema motiva nuestra definición. Omitimos la demostración.
Teorema 9.8.5.1
suponga que a, b y c son constantes (a ≠ 0), y f es continua por tramos en [0, ∞). con discontinuidades de salto en t1, . . . , tn, donde
0 < t1 < · · · < tn.
Sean k0 y k1 números reales arbitrarios. Entonces existe una única función y definida en [0, ∞) con las siguientes propiedades:
(a) y(0) = k0 y y′(0) = k1.
(b) y y y′ son continuas en [0, ∞).
(c) y′′ está definido en cada subintervalo abierto de [0, ∞) que no contiene ninguno de los puntos t1, . . . , tn, y
ay′′ + by′ + cy = f(t)
en cada uno de esos subintervalos.
(d) y′′ tiene límites por la derecha y por la izquierda en t1, . . . , tn. ♦
Definimos la función y del Teorema 9.8.5.1 como la solución del problema de valor inicial (9.8.5.1).}
Comenzamos considerando problemas de valor inicial de la forma
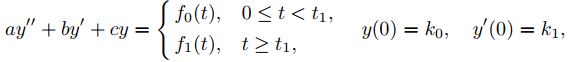 (9.8.5.2)
(9.8.5.2)
donde la función de forzamiento tiene una discontinuidad de un solo salto en t1.
♦ Podemos resolver (9.8.5.2) siguiendo estos pasos:
Paso 1. Encuentra la solución y0 del problema de valor inicial
Paso 2. Calcule c0 = y0(t1) y c1 = y0′ (t1)
Paso 3. Encuentre la solución y1 del problema de valor inicial
Paso 4. Obtenga la solución y de (9.8.5.2) como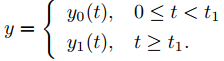
En el ejercicio 23 se muestra que y′ existe y es continua en t1. El siguiente ejemplo ilustra este procedimiento.
Ejemplo 9.8.5.1
Resolver el problema de valor inicial
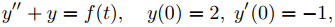 (9.8.5.3)
(9.8.5.3)
donde
Solución:
El problema de valor inicial en el Paso 1 es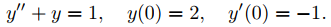
Te dejamos comprobar que su solución es
y0 = 1 + cos t − sen t.
Hacer el Paso 2 produce y0(π/2) = 0 y y0′ (π/2) = −1, por lo que el segundo problema de valor inicial es
Te dejamos comprobar que la solución de este problema es
y1 = −1 + cos t + sen t.
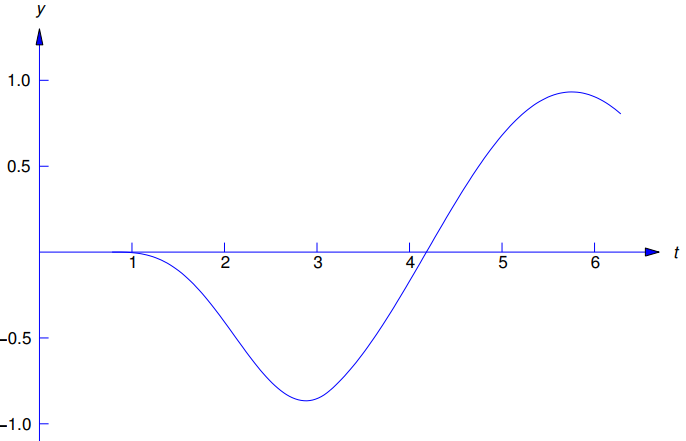
Por tanto, la solución de (9.8.5.3) es
 (9.8.5.4) ♦
(9.8.5.4) ♦

Figura 9.8.5.1 Gráfica de (9.8.5.4)
Si f0 y f1 están definidas en [0, ∞), podemos reescribir (9.8.5.2) como
y aplicar el método de las transformadas de Laplace. Ahora resolveremos el problema considerado en el Ejemplo 9.8.5.1 por este método.
Ejemplo 9.8.5.2
Utilice la transformada de Laplace para resolver el problema del valor inicial
 (9.8.5.5)
(9.8.5.5)
donde
Solución:
Aquí
entonces el Teorema 9.8.4.1 (con g(t) = 1) implica que
Por lo tanto, transformando (9.8.5.5) se obtiene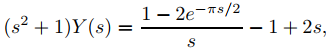
así que
 (9.8.5.6)
(9.8.5.6)
con
La forma para la expansión en fracciones parciales de G es
 (9.8.5.7)
(9.8.5.7)
Multiplicando por s(s2 + 1) se obtiene
o
Igualar coeficientes de potencias semejantes de s en los dos lados de esta ecuación muestra que A = 1, B = −A = −1 y C = 0. Por lo tanto, de (9.8.5.7),
Por lo tanto
De esto, (9.8.5.6), y el Teorema 9.8.4.2
Simplificando esto (recordando que cos(t − π/2) = sen t) se obtiene
o
que es el resultado obtenido en el ejemplo 9.8.5.1. ♦
COMENTARIO: No es obvio que usar la transformada de Laplace para resolver (9.8.5.2) como hicimos en el Ejemplo 9.8.5.2 produzca una función y con las propiedades establecidas en el Teorema 9.8.5.1; es decir, tales que y y y′ son continuas en [0, ∞) y y′′ tiene límites por la derecha y por la izquierda en t1. Sin embargo, esto es cierto si f0 y f1 son continuas y de orden exponencial en [0, ∞). En los ejercicios 9.8.6.11 a 9.8.6.13 se esboza una prueba.
Ejemplo 9.8.5.3
Resolver el problema de valor inicial
 (9.8.5.8)
(9.8.5.8)
donde
Solución:
Aquí
f(t) = t − u(t − 1)(t − 1),
entonces
Dado que transformando (9.8.5.8) se obtiene

donde
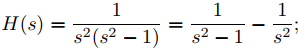 (9.8.5.9)
(9.8.5.9)
por lo tanto
h(t) = senh t − t. (9.8.5.10)
Ya que

concluimos de (9.8.5.9), (9.8.5.10) y el Teorema 9.8.4.1 que
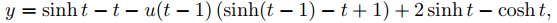
o
 (9.8.5.11)
(9.8.5.11)
Le dejamos a usted verificar que y e y′ son continuas y que y′′ tiene límites por la derecha y por la izquierda en t1 = 1. ♦
Ejemplo 9.8.5.4
Resolver el problema de valor inicial
y′′ + y = f(t), y(0) = 0, y′(0) = 0, (9.8.5.12)
Donde

Solución:
Aquí
f(t) = u(t − π/4) cos 2t − u(t − π) cos 2t,
entonces

Dado que transformando (9.8.5.12) se obtiene

observamos que
 (9.8.5.13)
(9.8.5.13)
donde
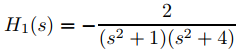 y
y 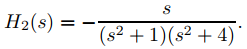 (9.8.5.14)
(9.8.5.14)
Para simplificar las expansiones en fracciones parciales requeridas, primero escribimos

Haciendo x = s2 y sustituyendo el resultado en (9.8.5.14) se obtiene

Las transformadas inversas son
 y
y 
De (9.8.5.13) y el Teorema 9.8.4.2,
 (9.8.5.15)
(9.8.5.15)
Ya que
y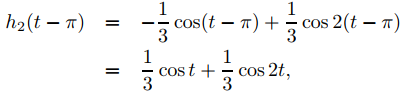
(9.8.5.15) se puede reescribir como

o
 (9.8.5.16)
(9.8.5.16)
Te dejamos a ti verificar que y y y′ son continuas y que y′′ tiene límites por la derecha y por la izquierda en t1 = π/4 y t2 = π. ♦

 (
(