| 9. Ecuaciones diferenciales | 9.5 Ecuaciones lineales de segundo orden |

9.5.7 Variación de parámetros

En esta sección damos un método llamado variación de parámetros para encontrar una solución particular de

P₀(x)y′′ + P₁(x)y′ + P₂(x)y = F(x)         (9.5.7.1)

si conocemos un conjunto fundamental {y₁, y₂} de soluciones de la ecuación complementaria

P₀(x)y′′ + P₁(x)y′ + P₂(x)y = 0        (9.5.7.2)

Habiendo encontrado una solución particular y_p por este método, podemos escribir la solución general de (9.5.7.1) como

y = y_p + c₁y₁ + c₂y₂.

      Dado que solo necesitamos una solución no trivial de (9.5.7.2) para encontrar la solución general de (9.5.7.1) por reducción de orden, es natural preguntarse por qué estamos interesados en la variación de parámetros, que requiere dos soluciones linealmente independientes de (9.5.7.2) para lograr el mismo objetivo. Aquí está la respuesta:

• Si ya conocemos dos soluciones linealmente independientes de (9.5.7.2), entonces la variación de parámetros probablemente será más simple que la reducción de orden.
• La variación de parámetros se generaliza naturalmente a un método para encontrar soluciones particulares de ecuaciones lineales de orden superior (Sección 9.9.4) y sistemas de ecuaciones lineales (Sección 9.10.7), mientras que la reducción de orden no lo hace.
• La variación de parámetros es una poderosa herramienta teórica utilizada por los investigadores en ecuaciones diferenciales. Aunque una discusión detallada de esto está más allá del alcance de estas lecciones, puede hacerse una idea de lo que significa en los Ejercicios 37 a 39.

      Ahora derivaremos el método. Como de costumbre, consideramos soluciones de (9.5.7.1) y (9.5.7.2) en un intervalo (a, b) donde P₀, P₁, P₂ y F son continuos y P₀ no tiene ceros. Suponga que {y₁, y₂} es un conjunto fundamental de soluciones de la ecuación complementaria (9.5.7.2). Buscamos una solución particular de (9.5.7.1) en la forma

y_p = u₁y₁ + u₂y₂         (9.5.7.3)

donde u₁ y u₂ son funciones a determinar para que y_p satisfaga (9.5.7.1). Puede que no creas que es una buena idea, ya que ahora hay dos funciones desconocidas por determinar, en lugar de una. Sin embargo, dado que u₁ y u₂ tienen que satisfacer solo una condición (que y_p sea una solución de (9.5.7.1)), podemos imponer una segunda condición que produce una simplificación conveniente, como sigue.

       Diferenciando (9.5.7.3), se obtiene

y_p′ = u₁y₁′ + u₂y₂′ + u₁′y₁ + u₂′y₂.         (9.5.7.4)

Como nuestra segunda condición en u₁ y u₂ requerimos que

u₁′y₁ + u₂′y₂ = 0.         (9.5.7.5)

Entonces (9.5.7.4) se convierte en

y_p′ = u₁y₁′ + u₂y₂′ ;         (9.5.7.6)

es decir, (9.5.7.5) nos permite derivar y_p (¡una vez!) como si u₁ y u₂ fueran constantes. Diferenciando (9.5.7.4), se obtiene

y_p′′ = u₁y₁′′ + u₂y₂′′ + u′₁y₁′ + u₂′y₂′ .         (9.5.7.7)

(No hay términos que involucren u₁′′ y u₂′′ aquí, como habría si no hubiéramos requerido (9.5.7.5).) Sustituyendo (9.5.7.3), (9.5.7.6) y (9.5 .7.7) en (9.5.7.1) y recopilando los coeficientes de u₁ y u₂ se obtiene

u₁(P₀y₁′′ + P₁y₁′ + P₂y₁) + u₂(P₀y₂′′ + P₁y₂′ + P₂y₂) + P₀(u₁′y₁′ + u₂′y₂′ ) = F.

Como en la derivación del método de reducción de orden, los coeficientes de u₁ y u₂ aquí son ambos cero porque y₁ e y₂ satisfacen la ecuación complementaria. Por lo tanto, podemos reescribir la última ecuación como

P₀(u₁′y₁′ + u₂′y₂′ ) = F.         (9.5.7.8)

Por lo tanto y_p en (9.5.7.3) satisface (9.5.7.1) si

       (9.5.7.9)

donde la primera ecuación es la misma que (9.5.7.5) y la segunda es de (9.5.7.8).

      Ahora le mostraremos que siempre puede resolver (9.5.7.9) para u₁′ y u₂′. (El método que usamos aquí siempre funcionará, pero los métodos más simples generalmente funcionan cuando se trata de ecuaciones específicas). Para obtener u₁′, multiplique la primera ecuación en (9.5.7.9) por y₂′ y la segunda ecuación por y₂. Esto produce

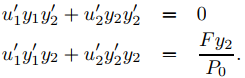
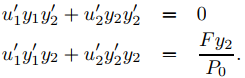
Restando la segunda ecuación de la primera se obtiene

      (9.5.7.10)

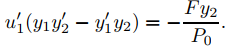
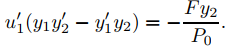
Como {y₁, y₂} es un conjunto fundamental de soluciones de (9.5.7.2) en (a, b), el teorema 9.5.1.6 implica que el wronskiano y₁y₂′ − y₁′y₂ no tiene ceros en (a, b). Por lo tanto podemos resolver (9.5.7.10) para u₁′, para obtener

        (9.5.7.11)

Le dejamos a usted comenzar desde (9.5.7.9) y demostrar con un argumento similar que

        (9.5.7.12)

      Ahora podemos obtener u₁ y u₂ integrando u₁′ y u₂′. Las constantes de integración pueden tomarse como cero, ya que cualquier elección de u₁ y u₂ en (9.5.7.3) será suficiente.

      No debe memorizar (9.5.7.11) y (9.5.7.12). Por otro lado, no desea volver a derivar todo el procedimiento para cada problema específico. Recomendamos:

(a) Escriba

y_p = u₁y₁ + u₂y₂             (9.5.7.13)

para recordarte lo que estás haciendo.

(b) Escriba el sistema

         (9.5.7.14)

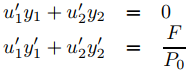
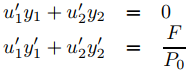
para el problema específico que está tratando de resolver.

(c) Resuelva (9.5.7.14) para u₁′ y u₂′ por cualquier método conveniente.

(d) Obtenga u₁ y u₂ integrando u₁′ y u₂′ , tomando las constantes de integración como cero.

(e) Sustituya u₁ y u₂ en (9.5.7.13) para obtener y_p.

Ejemplo ilustrativo 9.5.7.1

Encuentre una solución particular y_p de

x²y′′ − 2xy′ + 2y = x^9/2,         (9.5.7.15)

dado que y₁ = x  y  y₂ = x² son soluciones de la ecuación complementaria

x²y′′ − 2xy′ + 2y = 0

Luego encuentre la solución general de (9.5.7.15).

Solución:

Establecemos

y_p = u₁x + u₂x²,

donde

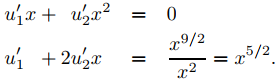
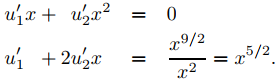
De la primera ecuación, u₁′ = −u₂′ x. Al sustituir esto en la segunda ecuación, se obtiene u₂′ x = x^5/2, por lo que u₂′  = x^3/2 y, por lo tanto, u₁′ = −u₂′ x = −x^5/2. Integrando y tomando las constantes de integración como cero, se obtiene

  y 

Por lo tanto

y la solución general de (9.5.7.15) es

♦

Ejemplo ilustrativo 9.5.7.2

Encuentre una solución particular y_p de

(x − 1)y′′ − xy′ + y = (x − 1)²,         (9.5.7.16)

dado que y₁ = x e y₂ = e^x son soluciones de la ecuación complementaria

(x − 1)y′′ − xy′ + y = 0.

Luego encuentre la solución general de (9.5.7.16).

Solución:

Establecemos

y_p = u₁x + u₂e^x,

donde

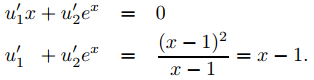
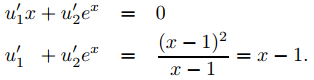
Al restar la primera ecuación de la segunda se obtiene −u₁′(x − 1) = x − 1, por lo que u₁′ = −1. De esta y la primera ecuación, u₂′ = −xe^−xu₁′ = xe^−x. Integrando y tomando las constantes de integración como cero, se obtiene

u₁ = −x   y   u₂ = −(x + 1)e^−x.

Por lo tanto

y_p = u₁x + u₂e^x = (−x)x + (−(x + 1)e^−x)e^x = −x² − x − 1,

por lo que la solución general de (9.5.7.16) es

y = y_p + c₁x + c₂e^x = −x² − x − 1 + c₁x + c₂e^x = −x² − 1 + (c₁ − 1)x + c₂e^x.       (9.5.7.17)

Sin embargo, dado que c₁ es una constante arbitraria, también lo es c₁ − 1; por lo tanto, mejoramos la apariencia de este resultado cambiando el nombre de la constante y escribiendo la solución general como

y = −x² − 1 + c₁x + c₂e^x.  ♦          (9.5.7.18)

      No hay nada de malo en dejar la solución general de (9.5.7.16) en la forma (9.5.7.17); sin embargo, creemos que estará de acuerdo en que (9.5.7.18) es preferible. También podemos ver la transición de (9.5.7.17) a (9.5.7.18) de manera diferente. En este ejemplo, la solución particular y_p = −x² − x − 1 contenía el término −x, que satisface la ecuación complementaria. Podemos eliminar este término y redefinir y_p = −x² − 1, ya que −x² − x − 1 es una solución de (9.5.7.16) y x es una solución de la ecuación complementaria; por lo tanto, −x² − 1 = (−x² − x − 1) + x también es una solución de (9.5.7.16). En general, siempre es legítimo descartar combinaciones lineales de {y₁, y₂} de soluciones particulares obtenidas por variación de parámetros. (Vea el Ejercicio 36 para una discusión general de esta pregunta). Haremos esto en los siguientes ejemplos y en las respuestas a los ejercicios que piden una solución particular. Por lo tanto, no se preocupe si su respuesta a tal ejercicio difiere de la nuestra solo por una solución de la ecuación complementaria.

Ejemplo ilustrativo 9.5.7.3

Encuentre una solución particular de

        (9.5.7.19)

Luego encuentra la solución general.

Solución:

El polinomio característico de la ecuación complementaria

y′′ + 3y′ + 2y = 0         (9.5.7.20)

es p(r) = r² + 3r + 2 = (r + 1)(r + 2), entonces y₁ = e^−x y y₂ = e^−2x forman un conjunto fundamental de soluciones de (9.5.7.20). Buscamos una solución particular de (9.5.7.19) en la forma

y_p = u₁e^−x + u₂e^−2x,

donde

Sumando estas dos ecuaciones se obtiene

  entonces 

De la primera ecuación,

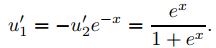
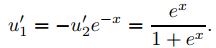
Integrando por medio de la sustitución v = e^x y tomando las constantes de integración como cero se obtiene

y

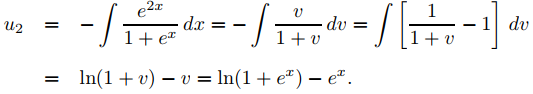
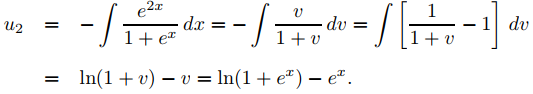
Por lo tanto

esto es 

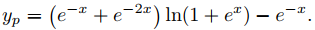
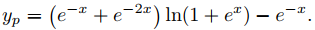
Dado que el último término de la derecha satisface la ecuación complementaria, lo descartamos y redefinimos

y_p = (e^−x + e^−2x) ln(1 + e^x).

La solución general de (9.5.7.19) es

♦

Ejemplo ilustrativo 9.5.7.4

Resolver el problema de valor inicial

  y(0) = −1, y′(0) = −5,         (9.5.7.21)

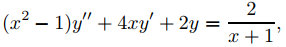
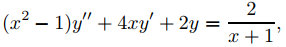
dado que

  y 

son soluciones de la ecuación complementaria

(x² − 1)y′′ + 4xy′ + 2y = 0.

Solución:

Primero usamos la variación de parámetros para encontrar una solución particular de

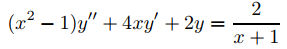
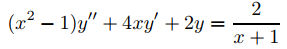
en (−1, 1) en la forma

donde

        (9.5.7.22)

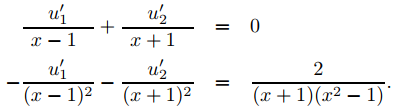
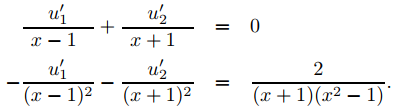
Multiplicando la primera ecuación por 1/(x − 1) y sumando el resultado a la segunda ecuación se obtiene

        (9.5.7.23)

Desde

(9.5.7.23) implica que u₂′ = 1. De (9.5.7.22),

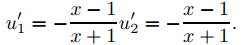
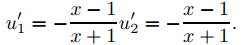
Integrando y tomando las constantes de integración como cero, se obtiene

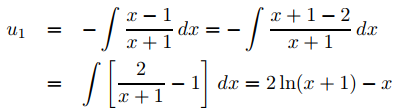
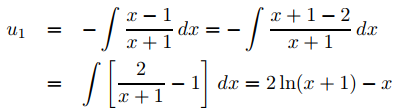
y

u₂ = ∫dx = x.

Por lo tanto

Sin embargo, desde

es una solución de la ecuación complementaria, redefinimos

Por tanto, la solución general de (9.5.7.24) es

        (9.5.7.24)

Diferenciando esto se obtiene

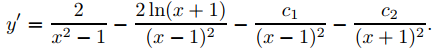
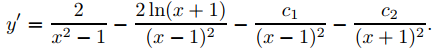
Haciendo x = 0 en las dos últimas ecuaciones e imponiendo las condiciones iniciales y(0) = −1 y y′(0) = −5 se obtiene el sistema

La solución de este sistema es c₁ = 2, c₂ = 1. Sustituyendo estos en (9.5.7.24) se obtiene

como la solución de (9.5.7.21). La figura 9.5.7.1 es una gráfica de la solución.  ♦

Figura 9.5.7.1

Comparación de métodos

Ahora hemos considerado tres métodos para resolver ecuaciones lineales no homogéneas: coeficientes indeterminados, reducción de orden y variación de parámetros. Es natural preguntarse qué método es mejor para un problema dado. El método de coeficientes indeterminados debe utilizarse para ecuaciones de coeficientes constantes con funciones forzadas que son combinaciones lineales de polinomios multiplicados por funciones de la forma e^αx, e^λxcosωx o e^λxsenωx. Aunque los otros dos métodos pueden usarse para resolver tales problemas, serán más difíciles excepto en los casos más triviales, debido a las integraciones involucradas.

      Si la ecuación no es una ecuación de coeficientes constantes o la función forzada no tiene la forma que se acaba de especificar, el método de coeficientes indeterminados no se aplica y la elección es necesariamente entre los otros dos métodos. Se podría argumentar que la reducción de orden es mejor porque requiere solo una solución de la ecuación complementaria, mientras que la variación de parámetros requiere dos. Sin embargo, la variación de parámetros probablemente será más fácil si ya conoce un conjunto fundamental de soluciones de la ecuación complementaria.