| 9. Ecuaciones diferenciales | 9.2. Ecuaciones diferenciales de primer orden | Ejercicios propuestos para el Capítulo 9.2.2 |

9.2.2 Ecuaciones separables

Una ecuación diferencial de primer orden es separable si se puede escribir como

h(y)y′ = g(x),          (9.2.2_1)          

donde el lado izquierdo es un producto de y′ y una función de y y el lado derecho es una función de x. Reescribir una ecuación diferencial separable en esta forma se llama separación de variables. En la Sección 9.2.1 usamos la separación de variables para resolver ecuaciones lineales homogéneas. En esta sección, aplicaremos este método a ecuaciones no lineales.

 Para ver cómo resolver (9.2.2_1), primero supongamos que y es una solución. Sean G(x) y H(y) antiderivadas de g(x) y h(y); es decir,

H′(y) = h(y)  y  G′(x) = g(x).          (9.2.2_2) 

Entonces, de la regla de la cadena,

Por lo tanto (9.2.2_1) es equivalente a

Integrando ambos lados de esta ecuación y combinando las constantes de integración se obtiene

H(y(x)) = G(x) + c.          (9.2.2_3)

Aunque derivamos esta ecuación asumiendo que y es una solución de (9.2.2_1), ahora podemos verla de manera diferente: cualquier función diferenciable y que satisfaga (9.2.2_3) para alguna constante c es una solución de (9.2.2_1).
Para ver esto, diferenciamos ambos lados de (9.2.2_3), usando la regla de la cadena en el miembro izquierdo, para obtener

que es equivalente a

debido a (9.2.2_2).

En conclusión, para resolver (9.2.2_1) basta con encontrar las funciones G = G(x)  y  H = H(y) que satisfagan (9.2.2_2). Entonces, cualquier función diferenciable y = y(x) que satisfaga (9.2.2_3) es una solución de (9.2.2_1).

Ejemplo ilustrativo 9.2.2_1

Resuelve la ecuación

y′ = x(1 + y²).

Solución:

Separando variables, se obtiene

Integrando, se obtiene

Por lo tanto

    ♦

Ejemplo ilustrativo 9.2.2_2

(a) Resuelva la ecuación

y′ = −x / y          (9.2.2_4)

(b) Resuelva el problema de valor inicial

y′ = −x / y,  y (1) = 1          (9.2.2_5)

(c) Resuelva el problema de valor inicial

y′ = −x / y,  y (1) = −2          (9.2.2_6)

Solución:

(a) Separando variables en (9.2.2_4), se obtiene

yy′ = −x

Integrando, se obtiene

y²/ 2 = −x²/2 + c  entonces  x² + y² = 2c

La última ecuación muestra que c debe ser positivo si y va a ser una solución de (9.2.2_4) en un intervalo abierto.
Por lo tanto, dejamos 2c = a² (con a > 0) y reescribimos la última ecuación como

x² + y² = a²          (9.2.2_7)

Esta ecuación tiene dos soluciones diferenciables para y en términos de x:

y = √(a² − x²),  −a < x < a          (9.2.2_8)

y

y = −√(a² − x²),  −a < x < a          (9.2.2_9)

Las curvas solución definidas por (9.2.2_8) son semicírculos sobre el eje x y las definidas por (9.2.2_9) son semicírculos debajo del eje x (Figura 9.2.2_1).

Figura 9.2.2_1 (a) y = √(2 − x²), −√2 < x < √2, (b) y = −√(5 − x²), −√5 < x < √5

(b) La solución de (9.2.2_5) es positiva cuando x = 1; por tanto, tiene la forma (9.2.2_8). Sustituyendo x = 1 e y = 1 en (9.2.2_7) para satisfacer la condición inicial se obtiene a² = 2; por tanto, la solución de (9.2.2_5) es

(c) La solución de (9.2.2_6) es negativa cuando x = 1 y, por lo tanto, tiene la forma (9.2.2_9). Sustituyendo x = 1 y y = −2 en (9.2.2_7) para satisfacer la condición inicial se obtiene a² = 5. Por tanto, la solución de (9.2.2_6) es

  ♦

Soluciones implícitas de ecuaciones separables

       En los ejemplos 9.2.2_1 y 9.2.2_2 pudimos resolver la ecuación H(y) = G(x) + c para obtener fórmulas explícitas para las soluciones de las ecuaciones diferenciales separables dadas. Como veremos en el siguiente ejemplo, esto no siempre es posible. En esta situación debemos ampliar nuestra definición de una solución de una ecuación separable. El siguiente teorema proporciona la base para esta modificación. Omitimos la demostración, que requiere un resultado de cálculo avanzado llamado teorema de función implícita.

Teorema 9.2.2.1

Suponga que g = g(x) es continua en (a, b) y h = h(y) es continua en (c, d). Sea G una antiderivada de g en (a, b) y sea H una antiderivada de h en (c, d). Sea x₀ un punto arbitrario en (a, b), sea y₀ un punto en (c, d) tal que h(y₀) ≠ 0, y defina

c = H(y₀) − G(x₀)       (9.2.2_10)

Entonces hay una función y = y(x) definida en algún intervalo abierto (a₁, b₁), donde a ≤ a₁ < x₀ < b₁ ≤ b, tal que y(x₀) = y₀  y

H(y) = G(x) + c          (9.2.2_11)

para a₁ < x < b₁. Por tanto, y es una solución del problema del valor inicial

h(y)y′ = g(x),  y(x₀) = y₀          (9.2.2_12)

 Es conveniente decir que (9.2.2_11) con c arbitrario es una solución implícita de h(y)y′ = g(x). Las curvas definidas por (9.2.2_11) son curvas integrales de h(y)y′ = g(x). Si c satisface (9.2.2_10), diremos que (9.2.2_11) es una solución implícita del problema de valor inicial (9.2.2_12). Sin embargo, tenga en cuenta estos puntos:

• Para algunas elecciones de c, puede que no haya funciones diferenciables y que satisfagan (9.2.2_11)
• La función y en (9.2.2_11) (no (9.2.2_11) en sí) es una solución de h(y)y′ = g(x).

Ejemplo ilustrativo 9.2.2_3

(a) Encuentre soluciones implícitas de

(b) Encuentre una solución implícita de

Solución:

(a) Separando de variables, se obtiene

(5y⁴ + 1)y′ = 2x + 1

La integración produce la solución implícita

y⁵ + y = x² + x + c.          (9.2.2_15)

de (9.2.2_13).

(b) Al imponer la condición inicial y(2) = 1 en (9.2.2_15) se obtiene 1 + 1 = 4 + 2 + c, entonces c = −4. Por lo tanto

y⁵ + y = x² + x − 4

es una solución implícita del problema del valor inicial (9.2.2_14).

Aunque más de una función diferenciable y = y(x) satisface 9.2.2_13) cerca de x = 1, se puede demostrar que solo hay una función que satisface la condición inicial y(1) = 2.

 La figura 9.2.2_2 muestra un campo direccional y algunas curvas integrales para (9.2.2_13).

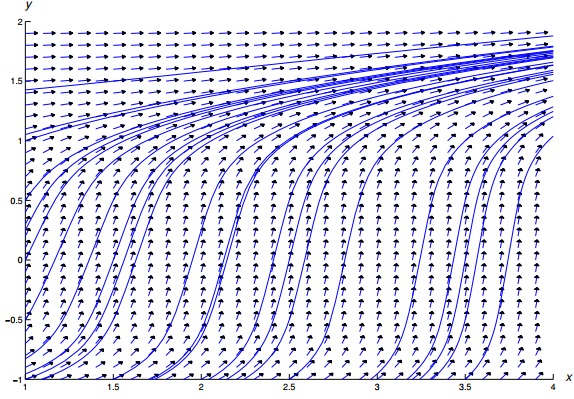
Figura 9.2.2_2 Un campo direccional y curvas integrales para y′ = (2x + 1)/(5y⁴ + 1)    ♦

Soluciones constantes de ecuaciones separables

Una ecuación de la forma

y′ = g(x) p(y)

es separable, ya que se puede reescribir como

Sin embargo, la división por p(y) no es legítima si p(y) = 0 para algunos valores de y. Los dos ejemplos siguientes muestran cómo abordar este problema.

Ejemplo ilustrativo 9.2.2_4

Encuentre todas las soluciones de

y′ = 2xy²          (9.2.2_16)

Solución:

Aquí debemos dividir por p(y) = y² para separar variables. Esto no es legítimo si y es una solución de (9.2.2_16) que es igual a cero para algún valor de x. Una de estas soluciones se puede encontrar mediante inspección: y ≡ 0. Ahora suponga que y es una solución de (9.2.2_16) que no es idénticamente cero. Dado que y es continua, debe haber un intervalo en el que y nunca sea cero. Dado que, en este caso, la división por y² es legítimo para toda x en este intervalo, podemos separar variables en (9.2.2_16) para obtener

Integrando, se obtiene

que es equivalente a

y = −1/(x² + c)          (9.2.2_17)

 Ahora hemos demostrado que si y es una solución de (9.2.2_16) que no es idénticamente cero, entonces y debe tener la forma (9.2.2_17). Al sustituir (9.2.2_17) en (9.2.2_16), puede verificar que (9.2.2_17) es una solución de (9.2.2_16).
Por tanto, las soluciones de (9.2.2_16) son y ≡ 0 y las funciones de la forma (9.2.2_17). Tenga en cuenta que la solución y ≡ 0 no tiene la forma (9.2.2_17) para ningún valor de c.

 La figura 9.2.2_3 muestra un campo de direcciones y algunas curvas integrales para (9.2.2_16)

Figura 9.2.2_3 Un campo direccional y curvas integrales para y′ = 2xy²

Ejemplo ilustrativo 9.2.2_5

Encuentre todas las soluciones de

y′ = (1/2)x(1 − y²)          (9.2.2_18)

Solución:

Aquí debemos dividir por p(y) = 1 − y² para separar variables. Esto no es legítimo si y es una solución de (9.2.2_18) que es igual a ± 1 para algún valor de x. Se pueden encontrar dos de estas soluciones mediante inspección:
y ≡ 1 y y ≡ −1. Ahora suponga que y es una solución de (9.2.2_18) tal que 1 − y² no es idénticamente cero. Dado que 1 − y² es continuo, debe haber un intervalo en el que 1 − y² nunca sea cero. Dado que la división por 1 − y² es legítima para toda x en ese intervalo, podemos separar las variables en (9.2.2.18) para obtener

Una expansión en fracciones parciales a la izquierda produce

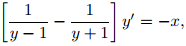
e integrando, se obtiene

por lo tanto,

Dado que y(x) ≠ ± 1 para x en el intervalo en discusión, la cantidad (y − 1)/(y + 1) no puede cambiar de signo en este intervalo. Por lo tanto, podemos reescribir la última ecuación como

donde c = ±eᵏ, dependiendo del signo de (y − 1)/(y + 1) en el intervalo. Resolviendo para y, se obtiene

Ahora hemos demostrado que si y es una solución de (9.2.2_18) que no es idénticamente igual a ± 1, entonces y debe ser como en (9.2.2_19). Sustituyendo (9.2.2_19) en (9.2.2_18) puede verificar que (9.2.2_19) es una solución de (9.2.2_18). Entonces, las soluciones de (9.2.2_18)) son y ≡ 1, y ≡ −1 y las funciones de la forma (9.2.2_19). Tenga en cuenta que la solución constante y ≡ 1 se puede obtener de esta fórmula tomando c = 0; sin embargo, la otra solución constante, y ≡ −1, no se puede obtener de esta manera.

 La figura 9.2.2_4 muestra un campo direccional y algunas integrales para (9.2.2_18).

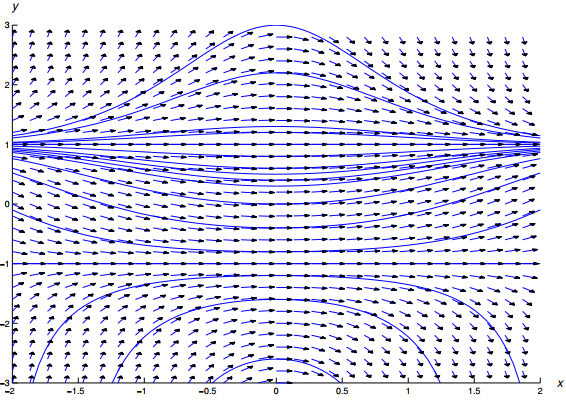
Figura 9.2.2_4 Un campo de direcciones y curvas integrales para y′ = (1/2)x(1 − y²)

Diferencias entre ecuaciones lineales y no lineales

El teorema 9.2.1.2 establece que si p y f son continuas en (a, b) entonces toda solución de

y′ + p(x) y = f (x)

en (a, b) se puede obtener eligiendo un valor para la constante c en la solución general, y si x₀ es cualquier punto en (a, b) y y₀ es arbitrario, entonces el problema de valor inicial

tiene una solución en (a, b).

Lo que no es cierto para las ecuaciones no lineales. Primero, vimos en los ejemplos 9.2.2_4 y 9.2.2_5 que una ecuación no lineal puede tener soluciones que no se pueden obtener eligiendo un valor específico de la constante que aparece en la familia de soluciones de un parámetro. En segundo lugar, en general es imposible determinar el intervalo de validez de una solución a un problema de valor inicial para una ecuación no lineal simplemente examinando la ecuación, ya que el intervalo de validez puede depender de la condición inicial. Por ejemplo, en el ejemplo 9.2.2_2 vimos que la solución de

es válida en (−a, a), donde a = √(x₀² + y₀²).

Ejemplo ilustrativo 9.2.2_6

Resuelva el problema del valor inicial

y′ = 2xy²,  y(0) = y₀

y determine el intervalo de validez de la solución.

Solución:

Primero suponga que y₀ ≠ 0. Por el ejemplo 9.2.2_4, sabemos que y debe tener la forma

y = −1/(x² + c)          (9.2.2_20)

La imposición de la condición inicial muestra que c = −1/y₀. Sustituyendo esto en (9.2.2_20) y reordenando los términos se obtiene la solución

Esta también es la solución si y₀ = 0. Si y₀ < 0, el denominador no es cero para ningún valor de x, por lo que la solución es válida en (−∞, ∞). Si y₀ > 0, la solución es válida solo en (−1/√y₀, 1/√y₀).    ♦