| 2. Límites y continuidad |
2.2. El límite de una función: Objetivos de aprendizaje
2.2.1. Usando la notación correcta, describa el límite de una función.
2.2.2. Use una tabla de valores para estimar el límite de una función o para identificar cuándo el límite no existe.
2.2.3. Use un gráfico para estimar el límite de una función o para identificar cuándo el límite no existe.
2.2.4. Defina límites unilaterales y proporcione ejemplos.
2.2.5. Explicar la relación entre los límites unilaterales y bilaterales.
2.2.6. Usando la notación correcta, describe un límite infinito.
2.2.7. Definir una asíntota vertical.
El concepto de un proceso límite o limitante, esencial para la comprensión del cálculo, ha existido durante miles de años. De hecho, los primeros matemáticos utilizaron un proceso limitante para obtener mejores aproximaciones de las áreas de los círculos. Sin embargo, la definición formal de límite, tal como la conocemos y entendemos hoy, no apareció hasta finales del siglo XIX. Por lo tanto, comenzamos nuestra búsqueda para comprender los límites, como lo hicieron nuestros antepasados matemáticos, utilizando un enfoque intuitivo. Al final de este capítulo, armados con una comprensión conceptual de los límites, examinamos la definición formal de límite.
Comenzamos nuestra exploración de límites observando las gráficas de las funciones
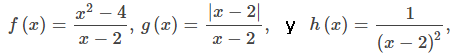
que se muestran en la figura 2.2_1. En particular, centramos nuestra atención en el comportamiento de cada gráfica en y alrededor de x = 2.
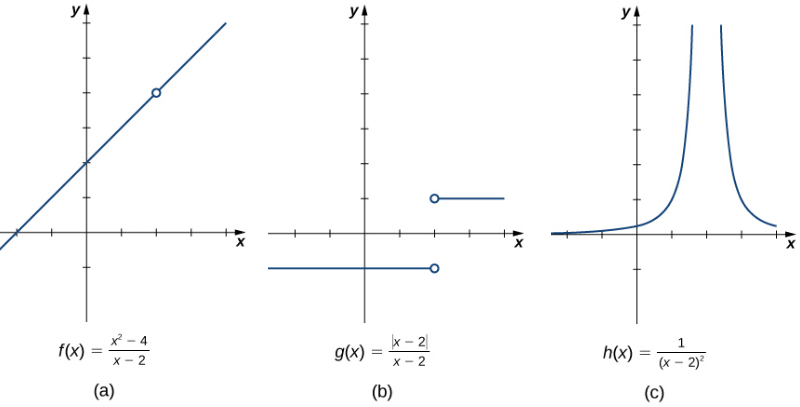
Cada una de las tres funciones no está definida en x = 2, pero si hacemos esta declaración y no otra, damos una imagen muy incompleta de cómo se comporta cada función en la vecindad de x = 2. Para expresar el comportamiento de cada gráfica en la vecindad de 2 más completamente, necesitamos introducir el concepto de límite.
Definición intuitiva de límite
Primero echemos un vistazo más de cerca a cómo se comporta la función f (x) = (x² − 4) / (x − 2) alrededor de x = 2 en la Figura 2.2_1. Observamos que conforme los valores de x se aproximan a 2 desde cualquier lado de 2, los valores de y = f (x) se aproximan a 4. Matemáticamente, decimos que el límite de f (x) a medida que x se acerca a 2 es 4. Simbólicamente, expresamos este límite como
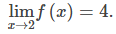
Desde este breve vistazo informal al concepto de límite, comencemos a desarrollar una definición intuitiva del límite de una función. Podemos pensar que el límite de una función en un número a es el número real L al que los valores funcionales se aproximan conforme los valores de la variable x se acercan a un número fijo a, siempre que exista dicho número real L. Expresado con más cuidado, tenemos la siguiente definición informal:
DEFINICIÓN informal e intuitiva de límite
|
Supongamos que f (x) sea una función definida en todos los valores de un intervalo abierto que contenga al número a, con la posible excepción de a, y que L sea un número real. Si los valores de la función f (x) se aproximan al número real L cuando los valores de x (≠ a) se aproximan al número a, entonces decimos que el límite de f (x) cuando x se aproxima a a es L. (Más sucinto , a medida que x se acerca a a, f (x) se aproxima y permanece cerca de L.) Simbólicamente, expresamos esta idea como |
Podemos estimar límites construyendo tablas de valores funcionales y observando la tendencia de los valores de la función y alternativa y complementariamente observando la gráfica de la función (mediante un software). Este proceso se describe en la siguiente estrategia.
ESTRATEGIA DE RESOLUCIÓN DE PROBLEMAS:
EVALUACIÓN DE UN LÍMITE UTILIZANDO UNA TABLA DE VALORES FUNCIONALES
1. Para estimar el valor de
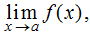
comenzamos completando una tabla de valores funcionales. Debemos elegir dos conjuntos de valores x: un conjunto de valores que se aproximen a a y menores que a, y otro conjunto de valores que se aproximen a a y mayores que a. La Tabla 2.2_1 muestra cómo se verían las tablas.
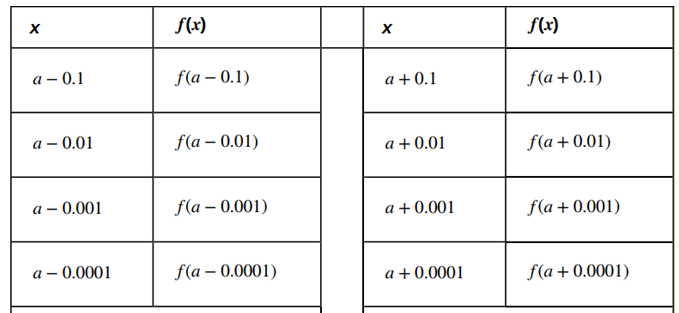
2. A continuación, observamos los valores en cada una de las columnas f (x) y determinemos si los valores parecen aproximarse a un valor único a medida que avanzamos hacia abajo en cada columna. En nuestra primera columna, observamos la secuencia de valores
f (a − 0.1), f (a − 0.01), f (a − 0.001), f (a − 0.0001, y así sucesivamente, y en la segunda columna observamos la secuencia de valores
f (a + 0.1), f (a + 0.01), f (a + 0.001), f (a + 0.0001), …
(Nota: aunque hemos elegido por conveniencia los valores de x: a ± 0.1, a ± 0.01, a ± 0.001, a ± 0.0001, etc., estos valores funcionarán casi siempre, y en muy raras ocasiones necesitaremos modificar estas elecciones).
3. Si los valores en ambas columnas se acercan a un valor común L, declaramos que parece que el

Podemos usar la siguiente estrategia para confirmar el resultado deducido a partir de la tabla o como un método alternativo para estimar un límite.
4. Usando una calculadora gráfica o software de computadora que nos permita graficar funciones, trazamos la gráfica de la función
f (x), asegurándonos de que los valores funcionales de f (x) para valores de x cerca de a estén en nuestra ventana visual.
Luego, usamos la opción de rastreo para movernos a lo largo de la gráfica y observar la lectura del valor para y cuando los valores de x se aproximan a a. Si los valores de y se acercan a L conforme nuestros valores x se acercan a a, desde ambas direcciones, entonces deducimos que probablemente

Es posible que necesitemos hacer zoom a nuestra gráfica y repetir este proceso varias veces.
Ejemplo ilustrativo 2.2_1 Evaluación de un límite utilizando una tabla de valores funcionales 1
Estime un valor de

usando una tabla de valores funcionales.
Solución:
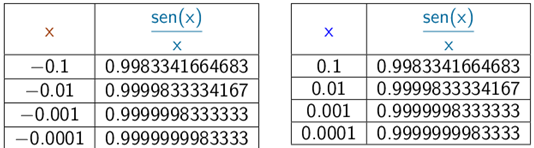
A medida que leemos cada columna senx/ x, vemos que los valores en cada columna parecen aproximarse a uno. Por lo tanto, es bastante razonable concluir que

La siguiente gráfica generada por computadora de f (x) = senx/ x confirma nuestra estimación:

Ejemplo ilustrativo 2.2_2 Evaluación de un límite utilizando una tabla de valores funcionales 2
Evalúe limx → 4 (√x − 2)/(x − 4) usando una tabla de valores funcionales.
Solución:
Como antes, usamos una tabla, en este caso, la Tabla 2.2_3, para anotar los valores de la función para los valores dados de x.
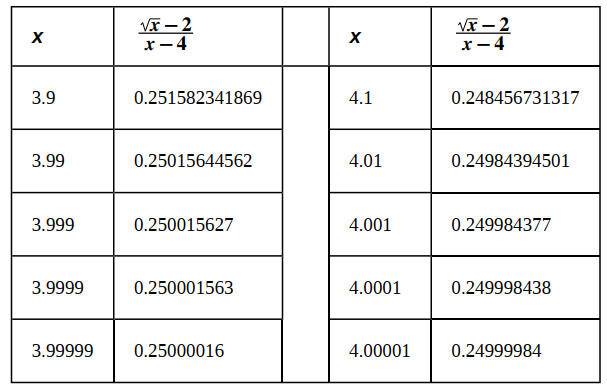
Después de inspeccionar esta tabla, vemos que los valores funcionales menores que 4 parecen estar disminuyendo hacia 0.25 mientras que los valores funcionales mayores que 4 parecen estar aumentando hacia 0.25. Concluimos que limx → 4 (√x − 2)/(x − 4) = 0.25. Confirmamos esta estimación usando la gráfica de f (x) = (√x − 2)/(x − 4) que se muestra en la Figura 2.2_3.

Ejercicio de control 2.2_1
Estime usando una tabla de valores funcionales. Use un gráfico para confirmar su estimación.
usando una tabla de valores funcionales. Use un gráfico para confirmar su estimación.
En este punto, vemos en el ejemplo 2.2_1 y en el ejemplo 2.2_2 que puede ser tan fácil, si no más fácil, estimar un límite de una función inspeccionando su gráfica en lugar de estimar el límite usando una tabla de valores funcionales. En el ejemplo 2.2_3, evaluamos un límite exclusivamente observando un gráfico en lugar de usar una tabla de valores funcionales.
Ejemplo ilustrativo 2.2_3 Evaluación de un límite usando un gráfico
Para g(x) que se muestra en la Figura 2.2_4, evalúe limx → −1 g(x).
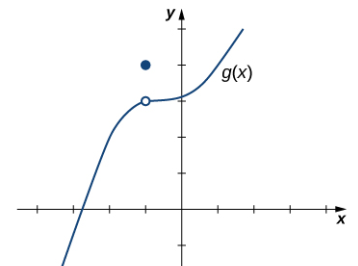
Solución:
A pesar de que g(−1) = 4, a medida que los valores de x se acercan a −1 desde cualquier lado, los valores de g(x) se acercan a 3. Por lo tanto, limx → −1 g(x) = 3. Tenga en cuenta que podemos determinar este límite sin siquiera saber la expresión algebraica de la función.
Con base en el ejemplo 2.2_3, hacemos la siguiente observación: es posible que el límite de una función exista en un punto y que la función se defina en este punto, pero el límite de la función y el valor de la función en el punto pueden ser diferentes.
Ejercicio de control 2.2_2
Use la gráfica de h(x) en la siguiente figura para evaluar limx → 2h(x), si es posible.
Observar una tabla de valores funcionales o ver la gráfica de una función nos proporciona información útil sobre el valor del límite de una función en un punto dado. Sin embargo, estas técnicas dependen demasiado de conjeturas. Eventualmente necesitamos desarrollar métodos alternativos de evaluación de límites. Estos nuevos métodos son de naturaleza más algebraica y los exploramos en la siguiente sección; sin embargo, en este punto presentamos dos límites especiales que son fundamentales para las técnicas por venir.
TEOREMA 2.2_1. Dos límites importantes
|
Si a es un número real y c una constante, entonces
|
Podemos hacer las siguientes observaciones sobre estos dos límites.
i. Para el primer límite, observe que a medida que x se aproxima a a, también lo hace f (x), porque f (x) = x.
En consecuencia, limx→a x = a.
ii. Para el segundo límite, considere la Tabla 2.2_4.
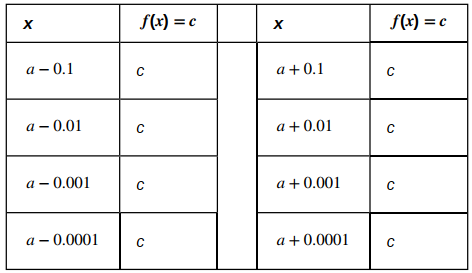
Observe que para todos los valores de x (independientemente de si se acercan a a, los valores de f (x) permanecen constantes en c. No tenemos más opción que concluir que limx→a c = c.

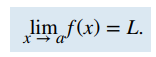
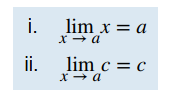
Enhorabuena! y muchas gracias por su blog, lo descubrí de manera casual y he encontrado una exposición clara concisa y concreta, de verdad que parece que la pantalla habla por sí sola. Un saludo!!
¡Gracias por tu maravillosa publicación! Realmente disfruté leyéndolo, podrías ser un gran autor. Siempre marcaré su blog y, a menudo, volveré por aquí. ¡Quiero animarlos a continuar con su gran trabajo, que tengan una buena noche!