| 9. Ecuaciones diferenciales | 9.7.Soluciones en serie de ecuaciones lineales de segundo orden |

9.7.7  El método de Frobenius III

En las Secciones 9.7.5 y 9.7.6 discutimos métodos para encontrar soluciones de Frobenius de una ecuación lineal homogénea de segundo orden cerca de un punto singular regular en el caso donde la ecuación indicial tiene una raíz repetida o raíces reales distintas que no difieren en un entero. En esta sección consideramos el caso donde la ecuación indicial tiene raíces reales distintas que difieren en un número entero. Limitaremos nuestra discusión a las ecuaciones que se pueden escribir como

x²(α₀ + α₁x)y′′ + x(β₀ + β₁x)y′ + (γ₀ + γ₁x)y = 0         (9.7.7.1)

o

x²(α₀ + α₂x²)y′′ + x(β₀ + β₂x²)y′ + (γ₀ + γ₂x²)y = 0,

donde las raíces de la ecuación indicial difieren en un entero positivo.

      Comenzamos con un teorema que proporciona un conjunto fundamental de soluciones de ecuaciones de la forma (9.7.7.1).

Teorema 9.7.7.1

Sea

L_y = x²(α₀ + α₁x)y′′ + x(β₀ + β₁x)y′ + (γ₀ + γ₁x)y,

donde α₀ ≠ 0, y definir

p₀(r) = α₀r(r − 1) + β₀r + γ₀,
p₁(r) = α₁r(r − 1) + β₁r + γ₁.

Suponga que r es un número real tal que p₀(n + r) es distinto de cero para todos los enteros positivos n, y defina

        (9.7.7.2)

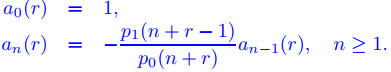
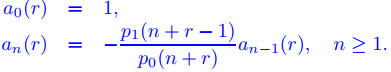
Sean r₁ y r₂ las raíces de la ecuación indicial p₀(r) = 0, y supongamos que r₁ = r₂ + k, donde k es un entero positivo. Entonces

es una solución de Frobenius de L_y = 0. Además, si definimos

      (9.7.7.3)

y

        (9.7.7.4)

entonces

        (9.7.7.5)

es también una solución de L_y = 0, y {y₁, y₂} es un conjunto fundamental de soluciones.  ♦

Prueba:

El Teorema 9.7.5.3 implica que L_y1 = 0. Ahora mostraremos que L_y2 = 0. Dado que L es un operador lineal, esto equivale a demostrar que

        (9.7.7.6)

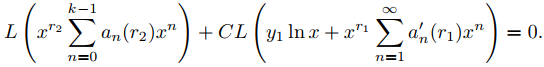
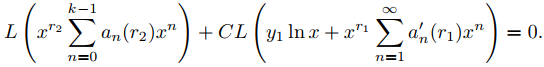
Para verificar esto, mostraremos que

        (9.7.7.7)

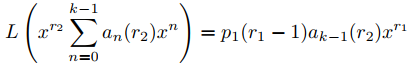
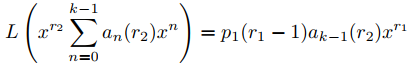
y

        (9.7.7.8)

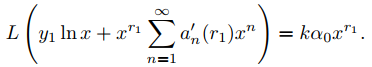
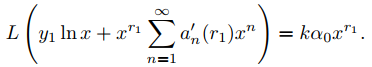
Esto implicará que L_y2 = 0, ya que sustituyendo (9.7.7.7) y (9.7.7.8) en (7.7.6) y usando (9.7.7.4) se obtiene

Probaremos (9.7.7.8) primero. Del Teorema 9.7.6.1,

Al establecer r = r₁ y recordar que p₀(r₁) = 0 y y₁ = y(x, r₁) se obtiene

        (9.7.7.9)

Dado que r₁ y r₂ son las raíces de la ecuación indicial, el polinomio indicial se puede escribir como

Diferenciando esto se obtiene

p′₀(r) = α₀(2r − r₁ − r₂).

Por lo tanto p′₀(r₁) = α₀(r₁ − r₂) = kα₀, entonces (9.7.7.9) implica (9.7.7.8).

Antes de probar (9.7.7.7), notamos primero que a_n(r₂) está bien definida por (9.7.7.3) para 1 ≤ n ≤ k − 1, ya que p₀(n + r₂) ≠ 0 para estos valores de n. Sin embargo, no podemos definir a_n(r₂) para n ≥ k con (9.7.7.3), ya que p₀(k + r₂) = p₀(r₁) = 0. Por conveniencia, definimos a_n(r₂) = 0 para n ≥ k. Entonces, del Teorema 9.7.5.1

        (9.7.7.10)

donde b₀ = p₀(r₂) = 0 y

b_n = p₀(n + r₂)a_n(r₂) + p₁(n + r₂ − 1)a_{n − 1}(r₂), n ≥ 1.

Si 1 ≤ n ≤ k − 1, entonces (9.7.7.3) implica que b_n = 0. Si n ≥ k + 1, entonces b_n = 0 porque a_{n − 1}(r₂) = a_n(r₂) = 0. Por lo tanto (9.7 .7.10) se reduce a

Como a_k(r₂) = 0 y k + r₂ = r₁, esto implica (9.7.7.7). 

Dejamos como ejercicio la demostración de que {y₁, y₂} es un conjunto fundamental (Ejercicio 41). ♦

Ejemplo ilustrativo 9.7.7.1

Encuentre un conjunto fundamental de soluciones de Frobenius de

2x²(2 + x)y′′ − x(4 − 7x)y′ − (5 − 3x)y = 0

Dé fórmulas explícitas para los coeficientes en las soluciones.

Solución:

Para la ecuación dada, los polinomios definidos en el Teorema 9.7.7.1 son

Las raíces de la ecuación indicial son r₁ = 5/2 y r₂ = −1/2, entonces k = r₁ − r₂ = 3. Por lo tanto, el Teorema 9.7.7.1 implica que

        (9.7.7.11)

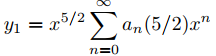
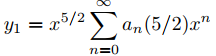
y

      (9.7.7.12)

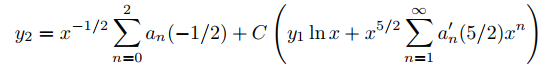
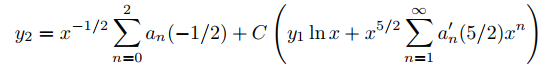
(con C como en (9.7.7.4)) forman un conjunto fundamental de soluciones de L_y = 0. La fórmula de recurrencia (9.7.7.2) es

        (9.7.7.13)

lo que implica que

        (9.7.7.14)

Por lo tanto

        (9.7.7.15)

Sustituyendo esto en (9.7.7.11) se obtiene

      Para calcular los coeficientes a₀(−1/2), a₁(−1/2) y a₂(−1/2) en y₂, establecemos r = −1/2 en (9.7.7.13) y aplicamos la fórmula de recurrencia resultante para n = 1, 2; de este modo,

La última fórmula da como resultado

a₁(−1/2) = 1/8  y  a₂(−1/2) = 3/32.

Sustituyendo r₁ = 5/2, r₂ = −1/2, k = 3 y α₀ = 4 en (9.7.7.4) se obtiene C = −15/128. Por lo tanto, de (9.7.7.12),

      (9.7.7.16)

Usamos diferenciación logarítmica para obtener a′_n(r). De (9.7.7.14),

Por lo tanto

Derivando con respecto a r, se obtiene

Por lo tanto

Estableciendo r = 5/2 aquí y recordando (9.7.7.15) se obtiene

        (9.7.7.17)

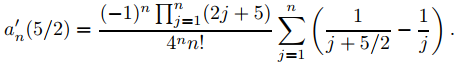
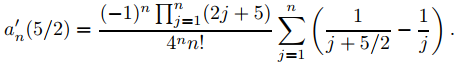
Ya que

Podemos reescribir (9.7.7.17) como

♦

        Si C = 0 en (9.7.7.4), no hay necesidad de calcular

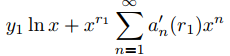
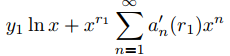
en la fórmula (9.7.7.5) para y₂. Por lo tanto, es mejor calcular C antes de calcular  Esto se ilustra en el siguiente ejemplo. (Véanse también los Ejercicios 44 y 45).

Ejemplo ilustrativo 9.7.7.2

Encuentre un conjunto fundamental de soluciones de Frobenius de

x²(1 − 2x)y′′ + x(8 − 9x)y′ + (6 − 3x)y = 0.

Dé fórmulas explícitas para los coeficientes en las soluciones.

Soluciones:

Para la ecuación dada, los polinomios definidos en el Teorema 9.7.7.1 son

Las raíces de la ecuación indicial son r₁ = −1 y r₂ = −6, entonces k = r₁ − r₂ = 5. Por lo tanto, el teorema 9.7.7.1 implica que

        (9.7.7.18)

y

        (9.7.7.19)

(con C como en (9.7.7.4)) forman un conjunto fundamental de soluciones de L_y = 0. La fórmula de recurrencia (9.7.7.2) es

        (9.7.7.20)

lo que implica que

        (9.7.7.21)

ya que

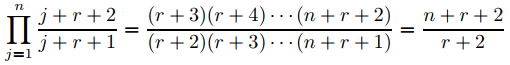
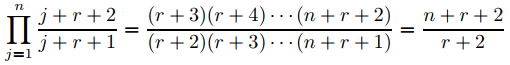
debido a cancelaciones, (9.7.7.21) se simplifica a

Por lo tanto

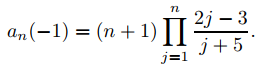
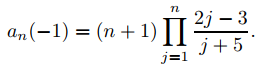
Sustituyendo esto en (9.7.7.18) se obtiene

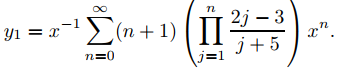
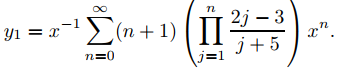
      Para calcular los coeficientes a₀(−6), . . ., a₄(−6) en y₂, establecemos r = −6 en (9.7.7.20) y aplicamos la fórmula de recurrencia resultante para n = 1, 2, 3, 4; de este modo,

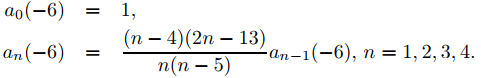
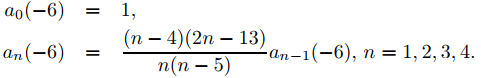
La última fórmula da como resultado

Como a₄(−6) = 0, (9.7.7.4) implica que la constante C en (9.7.7.19) es cero. Por lo tanto (9.7.7.19) se reduce a

♦

      Consideremos ahora ecuaciones de la forma

x²(α₀ + α₂x²)y′′ + x(β₀ + β₂x²)y′ + (γ₀ + γ₂x²)y = 0,

donde las raíces de la ecuación indicial son reales y difieren en un número entero par. El caso en que las raíces son reales y difieren en un número entero impar puede manejarse con el método que se analiza en .

      La demostración del siguiente teorema es similar a la demostración del Teorema 9.7.7.1 (Ejercicio 43).

Teorema 9.7.7.2

Sea

donde α₀ ≠ 0, y definamos

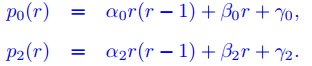
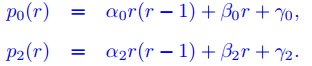
Supongamos que r es un número real tal que p₀(2m + r) es distinto de cero para todos los enteros positivos m, y definamos

        (9.7.7.22)

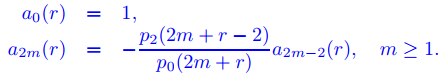
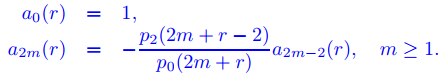
Sean r₁ y r₂ las raíces de la ecuación indicial p₀(r) = 0, y supongamos que r₁ = r₂ + 2k, donde k es un entero positivo. Entonces

es una solución de Frobenius de L_y = 0. Además, si definimos

y

        (9.7.7.23)

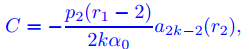
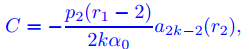
entonces

      (9.7.7.24)

es también una solución de Ly = 0, y {y₁, y₂} es un conjunto fundamental de soluciones.  ♦

Ejemplo ilustrativo 9.7.7.3

Encuentre un conjunto fundamental de soluciones de Frobenius de

x²(1 + x²)y′′ + x(3 + 10x²)y′ − (15 − 14x²)y = 0.

Dé fórmulas explícitas para los coeficientes en las soluciones.

Solución:

Para la ecuación dada, los polinomios definidos en el Teorema 9.7.7.2 son

p0(r) = r(r − 1) + 3r − 15 = (r − 3)(r + 5)
p2(r) = r(r − 1) + 10r + 14 = (r + 2)(r + 7).

Las raíces de la ecuación indicial son r₁ = 3 y r₂ = −5, entonces k = (r₁ − r2)/2 = 4. Por lo tanto, el Teorema 9.7.7.2 implica que

      (9.7.7.25)

y

(con C como en (9.7.7.23)) forman un conjunto fundamental de soluciones de L_y = 0. La fórmula de recurrencia (9.7.7.22) es

        (9.7.7.26)

lo que implica que

      (9.7.7.27)

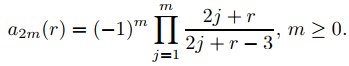
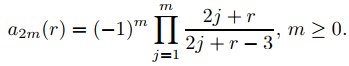
Por lo tanto

        (9.7.7.28)

Sustituyendo esto en (9.7.7.25) se obtiene

      Para calcular los coeficientes a₂(−5), a₄(−5) y a₆(−5) en y₂, establecemos r = −5 en (9.7.7.26) y aplicamos la fórmula de recurrencia resultante para m = 1, 2, 3; de este modo,

Esto produce

Sustituyendo r₁ = 3, r₂ = −5, k = 4 y α₀ = 1 en (9.7.7.23) se obtiene C = −3/16. Por lo tanto, de (9.7.7.24),

        (9.7.7.29)

      Para obtener a′_2m(r) usamos diferenciación logarítmica. De (9.7.7.27),

Por lo tanto

Derivando con respecto a r, se obtiene

Por lo tanto

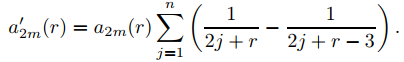
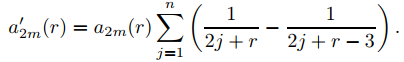
Poniendo r = 3 aquí y recordando (9.7.7.28) se obtiene

      (9.7.7.30)

dado que

Podemos reescribir (9.7.7.30) como

Sustituyendo esto en (9.7.7.29) se obtiene

♦

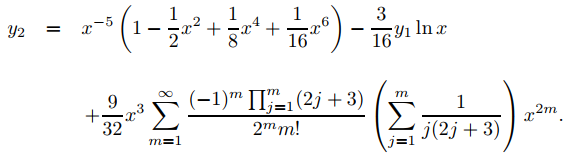
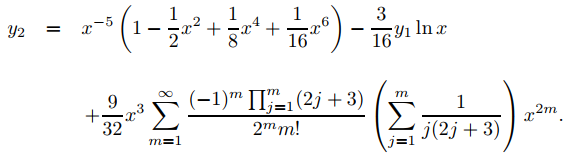
Ejemplo ilustrativo 9.7.7.4

Encuentre un conjunto fundamental de soluciones de Frobenius de

x²(1 − 2x²)y′′ + x(7 − 13x²)y′ − 14x²y = 0.

Dé fórmulas explícitas para los coeficientes en las soluciones.

Solución:

Para la ecuación dada, los polinomios definidos en el Teorema 9.7.7.2 son

Las raíces de la ecuación indicial son r₁ = 0 y r₂ = −6, entonces k = (r₁ − r₂)/2 = 3. Por lo tanto, el Teorema 9.7.7.2 implica que

        (9.7.7.31)

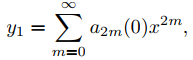
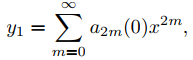
y

      (9.7.7.32)

con C como en (9.7.7.23)) forman un conjunto fundamental de soluciones de L_y = 0. Las fórmulas de recurrencia (9.7.7.22) son

        (9.7.7.33)

lo que implica que

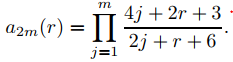
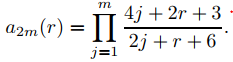
Establecer r = 0 produce

Sustituyendo esto en (9.7.7.31) se obtiene

        Para calcular los coeficientes a₀(−6), a₂(−6) y a₄(−6) en y₂, establecemos r = −6 en (7.7.33) y aplicamos la fórmula de recurrencia resultante para m = 1, 2; de este modo,

La última fórmula da como resultado

  y 

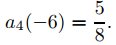
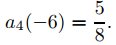
Como p₂(−2) = 0, la constante C en (9.7.7.23) es cero. Por lo tanto (9.7.7.32) se reduce a

♦