| 5. La integral y Técnicas de integración | Ejercicios propuestos del Capítulo 5.11 |

5.11 Fracciones parciales

Objetivos de aprendizaje:

5.11.1  Integrar una función racional utilizando el método de fracciones parciales.
5.11.2  Reconocer factores lineales simples en una función racional.
5.11.3  Reconocer factores lineales repetidos en una función racional.
5.11.4  Reconocer factores cuadráticos en una función racional.

    Hemos visto algunas técnicas que nos permiten integrar funciones racionales específicas. Por ejemplo, sabemos que

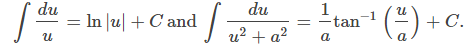
Sin embargo, todavía no tenemos una técnica que nos permita abordar cocientes arbitrarios de este tipo. Por ejemplo, no es inmediatamente obvio cómo evaluar

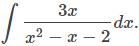
Sin embargo, sabemos por material desarrollado previamente que

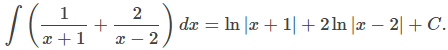
De hecho, al obtener un denominador común, vemos que

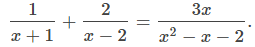
Por consiguiente,

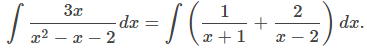
En esta sección, examinamos el método de descomposición de fracciones parciales, que nos permite descomponer funciones racionales en sumas de funciones racionales más simples y más fáciles de integrar. Con este método, podemos reescribir una expresión como: 3x/(x² − x − 2) como una expresión como 1/(x + 1) + 2/(x − 2).

La clave del método de descomposición en fracciones parciales es poder anticipar la forma que tomará la descomposición de una función racional. Como veremos, esta forma es predecible y altamente dependiente de la factorización del denominador de la función racional. También es extremadamente importante tener en cuenta que la descomposición de fracciones parciales se puede aplicar a una función racional P(x)/Q(x) solo si grado de P(x) es menor que el grado de Q(x). En el caso cuando grado (P(x)) ≥ grado (Q(x)), primero debemos realizar una división larga para reescribir el cociente P(x)/Q(x) en la forma A(x) + R(x)/Q(x), donde grado (R(x)) < grado (Q(x)). Luego hacemos una descomposición de fracciones parciales en R(x)/Q(x). El siguiente ejemplo, aunque no requiere descomposición de fracciones parciales, ilustra nuestro enfoque de las integrales de funciones racionales de la forma ∫P(x)/Q(x)dx, donde grado (P(x)) ≥ grado (Q(x)).

Ejemplo ilustrativo 5.11_1 Integrando ∫P(x)/Q(x)dx, donde grado (P(x)) ≥ grado (Q(x)).

Evalúe ∫(x² + 3x + 5)/(x + 1)dx.

Solución:
Como grado (x² + 3x + 5)  ≥ grado (x + 1), realizamos una división larga para obtener

de modo que,

♦

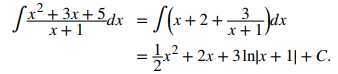Ejercicio de control 5.11.1

Evalúe $\int \frac{x \, – \, 3}{x + 2} \, dx$. ♦

Para integrar ∫P(x)/Q(x)dx, donde grado (P(x)) < grado (Q(x)), debemos comenzar factorizando Q(x).

Factores lineales no repetidos

Si Q(x) puede factorizarse como

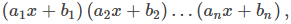
donde cada factor lineal es distinto, entonces es posible encontrar constantes

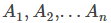
que satisfacen

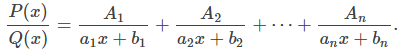
La prueba de que tales constantes existen está más allá del alcance de este curso.

En el siguiente ejemplo, vemos cómo usar fracciones parciales para integrar una función racional de este tipo.

Ejemplo ilustrativo 5.11_2 Fracciones parciales con factores lineales no repetidos

Evaluar

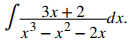
Solución:
Como grado (3x + 2) < grado (x³ − x² − 2x), comenzamos factorizando el denominador de (3x + 2)/(x³ − x² − 2x). Podemos ver que x³ − x² − 2x = x(x − 2) (x + 1). Por lo tanto, hay constantes A, B y C que satisfacen

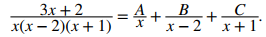
Ahora debemos encontrar el valor numérico de estas constantes. Para hacerlo, comenzamos obteniendo un denominador común a la derecha. Así,

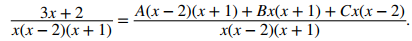
Ahora, establecemos los numeradores iguales entre sí, obteniendo

Hay dos estrategias diferentes para encontrar los valores numéricos de los coeficientes A, B y C. Nos referimos a estos como el método de igualar coeficientes y el método de sustitución estratégica.

REGLA 1: MÉTODO DE IGUALACIÓN DE COEFICIENTES Reescriba la ecuaciónEn la formaIgualar coeficientes produce el sistema de ecuacionesPara resolver este sistema, primero observamos que −2A = 2 ⇒ A = −1. Sustituir este valor en las dos primeras ecuaciones nos da el sistemaMultiplicar la segunda ecuación por −1 y sumar la ecuación resultante a la primera produceque a su vez implica que C = −1/3.  Al sustituir este valor en la ecuación B + C = 1 se obtiene B = 4/3. Por lo tanto, al resolver estas ecuaciones se obtiene A = −1, B = 4/3 y C = −1/3. Es importante tener en cuenta que el sistema producido por este método es consistente si y sólo si hemos configurado la descomposición correctamente. Si el sistema es inconsistente, hay un error en nuestra descomposición.   REGLA 2: MÉTODO DE SUSTITUCIÓN ESTRATÉGICA El método de sustitución estratégica se basa en el supuesto de que hemos configurado la descomposición correctamente. Si la descomposición está configurada correctamente, entonces debe haber valores de A, B y C que satisfaganpara todos los valores de x. Es decir, esta ecuación debe ser verdadera para cualquier valor de x que queramos sustituir. Por lo tanto, al elegir cuidadosamente los valores de x y sustituirlos en la ecuación, podemos encontrar fácilmente A, B y C. Por ejemplo, si sustituimos x = 0, la ecuación se reduce a 2 = A(−2)(1). Resolver para A produce A = −1. Luego, al sustituir x = 2, la ecuación se reduce a 8 = B(2)(3), o de manera equivalente B = 4/3. Por último, sustituimos x = −1 en la ecuación y obtenemos −1 = C(−1)(−3). Resolviendo, tenemos que C = −1/3. Es importante tener en cuenta que si intentamos utilizar este método con una descomposición que no se ha configurado correctamente, aún podemos encontrar valores para las constantes, pero estas constantes no tienen sentido. Si optamos por utilizar el método de sustitución estratégica, es una buena idea verificar el resultado recombinando los términos algebraicamente.

Ahora que tenemos los valores de A, B y C, reescribimos la integral original:

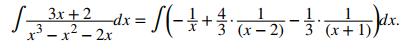
Evaluar la integral nos da♦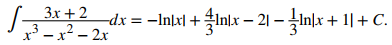

      En el siguiente ejemplo, integramos una función racional en la que el grado del numerador no es menor que el grado del denominador.

Ejemplo ilustrativo 5.11_3 Dividiendo antes de aplicar fracciones parciales

Evaluar

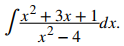
Dado que grado (x² + 3x + 1) ≥ grado (x² − 4), debemos realizar una división larga de polinomios. Esto resulta en

A continuación, realizamos descomposición de fracción parcial en

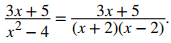
Tenemos que

De tal modo que

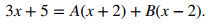
Resolviendo para A y B usando cualquier método, obtenemos A = 11/4 y B = 1/4.
Reescribiendo la integral original, tenemos

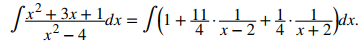
Evaluar la integral produce

♦

       Como veremos en el siguiente ejemplo, puede ser posible aplicar la técnica de descomposición de fracción parcial a una función no racional. El truco es convertir la función no racional en una función racional mediante una sustitución.

Ejemplo ilustrativo 5.11_4 Aplicar fracciones parciales después de una sustitución

Evaluar

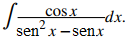
Solución:
Comencemos dejando u = senx. En consecuencia, du = cosxdx. Después de hacer estas sustituciones, tenemos

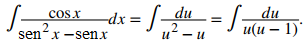
La aplicación de la descomposición de fracción parcial a 1/u(u − 1) da

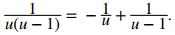
De tal manera que,

♦

Ejercicio de control 5.11.2

Evalúe $\int \frac{x + 1}{(x + 3)(x \, – \, 2)} \, dx$. ♦

Factores lineales repetidos

Para algunas aplicaciones, necesitamos integrar expresiones racionales que tengan denominadores con factores lineales repetidos, es decir, funciones racionales con al menos un factor de la forma (ax + b)ⁿ, donde n es un entero positivo mayor o igual a 2 Si el denominador contiene el factor lineal repetido (ax + b)ⁿ, entonces la descomposición debe contener

Como veremos en nuestro próximo ejemplo, la técnica básica utilizada para resolver los coeficientes es la misma, pero requiere más álgebra para determinar los valores de los numeradores de las fracciones parciales.

Ejemplo ilustrativo 5.11_5 Fracciones parciales con factores lineales repetidos

Solución:
Tenemos que grado (x − 2) < grado ((2x − 1)² (x − 1)), por lo que podemos proceder con la descomposición. Dado que (2x − 1)² es un factor lineal repetido, incluya

en la descomposición Así,

Después de obtener un denominador común e igualar los numeradores, tenemos

Luego usamos el método de igualar coeficientes para encontrar los valores de A, B y C.

Los igualación de coeficientes produce 2A + 4C = 0, −3A + B − 4C = 1 y A − B + C = −2. La solución de este sistema es A = 2, B = 3 y C = −1.

Alternativamente, podemos usar el método de sustitución estratégica. En este caso, la sustitución de x = 1 y x = 1/2 en la ecuación  produce fácilmente los valores B = 3 y C = −1. En este punto, puede parecer que nos hemos quedado sin buenas opciones para x, sin embargo, dado que ya tenemos valores para B y C, podemos sustituir estos valores y elegir cualquier valor para x que no se haya utilizado previamente. El valor x = 0 es una buena opción. En este caso, obtenemos la ecuación −2 = A(−1)(−1) + 3(−1) + (−1)(−1)² o, de manera equivalente, A = 2.
Ahora que tenemos los valores para A, B y C, reescribimos la integral original y la evaluamos:

♦

Ejercicio de control 5.11.3

Configure la descomposición en fracciones parciales para $\int \frac{x + 2}{(x + 3)^3 (x \, – \, 4)^2} \, dx$. (No resuelva para los coeficientes ni complete la integración). ♦

El método general

Ahora que estamos comenzando a tener la idea de cómo funciona la técnica de descomposición en fracciones parciales, describamos el método básico en la siguiente estrategia de resolución de problemas.

ESTRATEGIA DE RESOLUCIÓN DE PROBLEMAS: DESCOMPOSICIÓN EN FRACCIONES PARCIALES

Para descomponer la función racional P(x)/Q(x) en una suma de fracciones parciales, utilice los siguientes pasos: 1.  Asegúrese de que el grado (P(x)) < grado (Q(x)). Si no, realice una división larga de polinomios. 2. Factoriza Q(x) en el producto de factores cuadráticos lineales e irreductibles. Un cuadrático irreducible es un cuadrático que no tiene ceros reales. 3. Suponiendo que el grado (P(x)) < grado (Q(x)), los factores de Q(x) determinan la forma de la descomposición de P(x)/Q(x).     a.  Si Q(x) se puede factorizar como (a₁x + b₁) (a₂x + b₂) … (anx + bn), donde cada factor lineal es distinto, entonces es posible encontrar constantes A₁, A₂, … An satisfaciendo      b.  Si Q(x) contiene el factor lineal repetido (ax + b)ⁿ, entonces la descomposición debe contener      c.  Para cada factor cuadrático irreducible ax² + bx + c que contiene Q(x), la descomposición debe incluir      d.  Para cada factor cuadrático irreducible repetido (ax² + bx + c)ⁿ, la descomposición debe incluir      e. Después de determinar la descomposición apropiada, obtenga el valor numérico de las constantes.      f. Por último, reescriba la integral en su forma de descomposición en fracciones parciales y evalúela utilizando técnicas desarrolladas previamente o fórmulas de integración.

Factores cuadráticos simples

Ahora echemos un vistazo a la integración de una expresión racional en la que el denominador contiene un factor cuadrático irreducible. Recuerde que el trinomio ax² + bx + c es irreducible en los reales si la ecuación ax² + bx + c = 0 no tiene ceros reales, es decir, si b² − 4ac < 0.

Ejemplo ilustrativo 5.11_6 Expresiones racionales con un factor cuadrático irreducible

Evalúe

Solución:
Como grado (2x − 3) < grado (x³ + x), factorice el denominador y proceda con la descomposición en fracciones parciales. Como x³ + x = x(x² + 1) contiene el factor cuadrático irreducible x² + 1, incluya el término

como parte de la descomposición, junto con C/x para el término lineal x. Por lo tanto, la descomposición tiene la forma

Después de obtener un denominador común e igualar los numeradores, obtenemos la ecuación

Resolviendo para A, B y C, obtenemos A = 3, B = 2 y C = −3.
Así,

Sustituyendo de nuevo en la integral, obtenemos

Nota: Podemos reescribir ln∣x² + 1∣ = ln(x² + 1), si deseamos hacerlo, ya que x² + 1 > 0. ♦

Ejemplo ilustrativo 5.11_7 Fracciones parciales con un factor cuadrático irreducible

Evaluar

Solución:
Podemos comenzar factorizando x³ − 8 = (x − 2)(x² + 2x + 4). Vemos que el factor cuadrático x² + 2x + 4 es irreducible ya que 2² − 4 (1)(4) = – 12 < 0. Usando la descomposición descrita en la estrategia de resolución de problemas, obtenemos

Después de obtener un denominador común y equiparar los numeradores, esto se convierte en

Aplicando cualquiera de estos métodos, obtenemos A = 1/12, B = −1/12 y C = −1/3.
Reescribiendo la integral dada, obtenemos

Podemos observar inmediatamente que

pero con la integral

se requiere un poco más de esfuerzo. Comencemos completando el
cuadrado en x² + 2x + 4 para obtener

Al dejar u = x + 1 y consecuentemente du = dx, vemos que

Sustituir de nuevo en la integral original y simplificar da

Aquí nuevamente, podemos omitir el valor absoluto si lo deseamos, ya que x² + 2x + 4 > 0 para todo x. ♦

Ejemplo ilustrativo 5.11_8  Encontrar un volumen

Encuentre el volumen del sólido de revolución obtenido al girar la región encerrada en la gráfica de

y el eje x sobre el intervalo [0, 1] alrededor del eje y.

Solución:
Comencemos dibujando la región a girar (ver Figura 5.11_1). Del boceto, vemos que el método de rebanadas es una buena opción para resolver este problema.

Figura 5.11_1 Podemos usar el método de rebanadas para encontrar el volumen de revolución obtenido al girar la región que se muestra alrededor del eje y.

El volumen del sólido viene dado por

Dado que grado ((x² + 1)²) = 4 > 3 = grado (x³), podemos proceder con la descomposición en fracciones parciales. Tenga en cuenta que (x² + 1)² es una cuadrática irreducible repetida. Usando la descomposición descrita en la estrategia de resolución de problemas, obtenemos

Encontrar un denominador común y equiparar los numeradores da

Resolviendo, obtenemos A = 1, B = 0, C = −1 y D = 0. Sustituyendo de nuevo en la integral, tenemos

\[ \begin{align*} V &= 2\pi \int_{0}^{1} \frac{x^3}{(x^2+1)^2} dx \\ &= 2\pi \int_{0}^{1} \left( \frac{x}{x^2+1} – \frac{x}{(x^2+1)^2} \right) dx \\ &= 2\pi \left( \frac{1}{2}ln(x^2 + 1) + \frac{1}{2} \cdot \frac{1}{x^2+1} \right) \Bigg|_0^1 \\ &= \pi \left( ln2 – \frac{1}{2} \right) . \end{align*} \]

♦

Ejercicio de control 5.11.4

Configure la descomposición en fracciones parciales para $\int \frac{x^2 + 3x + 1}{(x + 2)(x \, – \, 3)^2 (x^2 + 4)^2} \, dx$. ♦